XiaoMi-AI文件搜索系统
World File Search System第一年 B TECH 课程结构 2024- ...
用数值方法求解方程。• CO5:应用插值概念求解数值微分和积分问题。教学大纲:矩阵代数:基本列变换和行变换、通过基本行运算求逆矩阵、矩阵的梯形和秩、线性方程组:一致性、高斯消元法、高斯-乔丹法、雅可比法和高斯-赛德尔法求解、特征值和特征向量:基本性质、谱矩阵分解、对角化、矩阵的幂。向量空间:向量概念向高维的推广、广义向量运算、向量空间和子空间、线性独立性和跨度、基。内积空间和 Gram-Schmidt 正交化过程。线性变换。微分方程及应用:一阶和高阶线性微分方程。用逆微分算子、参数变分法和待定系数法求解齐次和非齐次线性方程。代数和超越方程的解:参数曲线的追踪:摆线和相关曲线。二分法、试位法、牛顿-拉夫森法。用牛顿-拉夫森法求解非线性方程组。插值:有限差分和除差分。牛顿-格雷戈里和拉格朗日插值公式。牛顿除差插值公式。离散数值微分、数值积分:梯形法则、辛普森 1/3 法则和辛普森 3/8 法则。常微分方程的数值解:泰勒级数法、修正欧拉法、龙格-库塔法。参考书:
第一年精神病学训练比赛2024
我们的服务怜悯心理健康是一项迅速扩展的服务,可满足墨尔本大都会西南部分区的各种公共心理健康需求。该组织位于城市附近,雇用来自许多文化和背景的人们,无论他们的信念如何,他们都有共同的纽带来照顾有需要的人。我们的计划Mercy Health很高兴能提供5个第一年/第1阶段的精神病学注册表培训职位,该职位于2025年2月开始,在RANZCP培训的三个阶段进行了其他多次培训轮换。MMH精神病学培训计划提供了所有强制性轮换,并为注册服务商提供了在该州最广泛的围产期心理健康服务处工作的机会。第一年的住院轮换位于我们在Werribee的新的54床Clare Moore大楼中,并受到热衷于教学的全职认可的主管的监督。其他心理健康旋转包括:
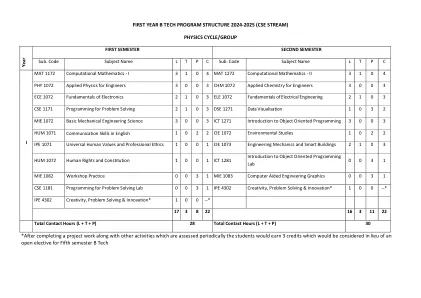
第一年教学大纲W.E.F. 2024-25
生物技术通常被认为是应对未来挑战的希望技术,例如养活我们的人口增加,清理危险的污染环境和增强医疗保健部门等。建立新的IISER,中央大学和IIT表明我们已经在发展基础设施和人力资源。,如果没有生物技术和包容性的努力,我们成为未来的“超级大国”的梦想将是不可能的。因此,有必要吸引年轻而聪明的学生并在生物技术领域进行训练。
经济前景是否如一年前预测的那样发展?
在劳动力市场,移民人数的增加推动了就业增长速度快于预期,而就业人口比率仍保持在历史高位,这得益于极高的职位空缺水平。与此相符的是,失业率的演变与过去一年的预期基本一致(图 B.4)。失业率和更广泛的闲置产能指标都表明,自 2022 年底以来,劳动力市场已经变得不那么紧张。与此相关的是,工资增长的演变与一年前的预测基本一致(图 B.5)。人口增长强于预期的供需效应似乎在总体上已经大致抵消,同时有助于缓解特定行业(如酒店业)的劳动力短缺。这有助于遏制一些受影响行业和地区的工资压力,尽管移民人数的增加并没有对总工资增长产生实质性影响。
第一年教学大纲W.E.F. 2024-25
牢记生物技术和生物信息学的BOS准备了课程,以确保对职业生物技术的最新水平。研究职业生物技术为学生做好准备,以使他们的职业在教育机构或可以直接参与教学,研发和发展的行业中工作。此外,为了确保统一的课程及其在UG/PG级别的质量,不同印度大学的课程,Net,Set,Set,MPSC和UPSC的课程以及UGC模型课程被称为更新相同的基础。
一年级语言艺术与读写能力英语...
一年级 英语创新途径中的语言艺术和读写能力 一年级的学生通过平衡的读写能力方法培养阅读和语言艺术技能。学生将沉浸在国家地理阅读计划中,并将学习如何在全年课程中运用技能阅读真实的文学和信息文本。重点是学习必要的基础技能,以在各种情况下培养和加强理解力。学生将建立词汇和语法知识,以提高口语和书面语言能力。年级写作包括回应文学作品、创作叙事以及说明性/信息性作品。引人入胜的写作活动专注于写作过程、应用拼写规则和标准英语的惯例。学生将学会:
第一年工学学士学位课程的共同课程...
模块3[8L] 数列和级数:数列和级数收敛的基本概念;收敛检验:比较检验、柯西根检验、达朗贝尔比检验(这些检验的语句和相关问题)、拉贝检验;交错级数;莱布尼茨检验(仅语句);绝对收敛和条件收敛。 模块4[10L] 多元函数微积分:多元函数简介;极限和连续性、偏导数、三元以下齐次函数和欧拉定理、链式法则、隐函数的微分、全微分及其应用、三元以下雅可比矩阵最大值、最小值;函数的鞍点;拉格朗日乘数法及其应用;线积分的概念,二重和三重积分。模块 5[10L] 向量微积分:标量变量的向量函数,向量函数的微分,标量和向量点函数,标量点函数的梯度,向量点函数的散度和旋度,
第一年荣誉人文研讨会,WRTR 2305
本课程将向学生介绍更大的达拉斯环境,并以不同的方式研究城市和一个地区。主要目的是发展学生对大达拉斯人的人民,机构和地点的了解,并知道它们之间的关系。该课程将向学生介绍多种纪律观点,以及如何使用这些观点来发展对单个大都市地区的复杂而复杂的理解。在课程结束时,学生将展示至少有两种理解城市的纪律方法。通过每周的课堂讨论,书面作业,考试和小组项目,学生将证明他们的能力阅读,写作和仔细,批判性地讲话以及进行主要研究。
计算机视觉中的最后一年博士候选人
2022 : Honorable Mention for NDSEG Fellowship 2021 : Jacobs School of Engineering Fellowship (UC San Diego) 2021 : Elected to Phi Beta Kappa and Sigma Xi (Williams College) 2020 : Robert G. Wilmers Jr. 1990 Fellowship 2020 : Williams College Summer Research Fellowship 2019 : John Houghton Harris Memorial Scholarship 2018 : Alumni-Sponsored实习计划赠款2017年:阿默斯特学院Schupf研究奖学金($ 20,000提名)
一年AC One Planet Eltif首先ELTIF 2.0套...
是专门从事可持续真正资产投资的资产经理。自2007年以来,我们一直在提供引人注目的投资机会,以推动能源过渡和可持续基础设施。我们的目标是在支持清洁能源计划的同时提供弹性的回报,并促进全球基础设施的脱碳。