XiaoMi-AI文件搜索系统
World File Search System时间谐波最佳控制问题的确切而近似的Schur补体方法
在[1,7]中的时间依赖性通过截短的傅立叶膨胀来处理,这使我们能够为每个频率获得单独的线性系统。在那里,提出了有效的求解线性系统的预处理方法,其中预核心是具有区块 - diagonal的,并且是较低的三角形形式。在[2]中使用了完整的两二个块结构的预处理,进一步称为PRESB,在续集中定义。[3]中的研究提供了不同结构的预处理(遮挡型,块 - 三角形和PRESB形式)之间的比较。比较是根据相应预处理矩阵及其数值性能的光谱正确的。数值实验表明,相对于正则化参数的频率范围,问题大小和值,PERB形式的预处理更加健壮。可以在[10]中找到对这些预调节器和一些修改形式的信息。[9]研究中的工作又是块形式形式的另一个预处理,并分析了双重预处理,适合于离散状态的向量形式。在[8]中考虑了(2)的非线性形式,其中为线性化问题提出了完整的两乘两块形式的预处理,可以将其分解和解决,以块 - 二进制预处理的成本,并且相对于问题大小和测试频率的范围是可靠的。
技术教育CET教学大纲2024-25
标准)●代数:代数,扩展,分解,二次方程,指数,对数,算术,几何和谐波进程,二项式定理,排列和组合的基本操作。●坐标几何形状:矩形笛卡尔坐标,线的方程,中点,相交等等,圆的方程,距离公式,一对直线,抛物线,抛物线,椭圆形和双曲线,简单的几何形状,简单的几何变换,例如翻译,旋转,量表,缩放,尺度。●微分方程:一阶的微分方程及其解,线性微分方程具有恒定系数,均匀的线性微分方程。●三角学:简单的身份,三角方程,三角形的特性,三角形解决方案,高度和距离,逆函数。●概率和统计:概率理论的基本概念,平均值,依赖和独立事件,频率分布以及分散,偏斜和峰度,随机变量和分布功能,数学期望,二项式,POISSON,POISSON,正常分布,正常分布,曲线拟合以及最小二乘的智慧和智慧的Squares,corle&Repartration,corpar和Recorpration和Recorpration。●算术:比率和比例,时间工作问题,距离速度,百分比等。●基本集合理论和功能:集合,关系和映射。●测量:圆,体积和表面积的区域,三角形和四边形,圆周和圆周,例如立方体,球体,圆柱体和锥体。b)逻辑 /抽象推理:这将包括衡量您可以思考的速度和逻辑的问题。
Trimble TSC5
© 2021–2022,Trimble Inc. 保留所有权利。Trimble 和地球与三角形徽标是 Trimble Inc. 在美国和其他国家/地区注册的商标。Access 是 Trimble Inc. 的商标。蓝牙文字标记和徽标归 Bluetooth SIG, Inc. 所有,Trimble Inc. 对此类标记的任何使用均已获得许可。Android、Google 和 Google Play 是 Google LLC 的商标。所有其他商标均为其各自所有者的财产。PN 022516-528A(05/22)
Trimble TSC5
© 2021–2022,Trimble Inc. 保留所有权利。Trimble 和地球与三角形徽标是 Trimble Inc. 在美国和其他国家/地区注册的商标。Access 是 Trimble Inc. 的商标。蓝牙文字标记和徽标归 Bluetooth SIG, Inc. 所有,Trimble Inc. 对此类标记的任何使用均已获得许可。Android、Google 和 Google Play 是 Google LLC. 的商标。所有其他商标均为其各自所有者的财产。PN 022516-528A (05/22)
变换:AEDP期刊
Annika Medbo摘要:本文为我的工作提供了我的工作,该患者的自我意识深刻没有成长,需要在国家领域中进行广泛的参与。AEDP的指导精神 - 通过跟踪展开现象学来创建我们的干预措施,使我能够在AEDP框架内进行创新。在与这个客户的工作过程中,我设计了两个新的经验三角:发现和拯救自我的三角形以及新兴自我的三角形。这些三角形提供了主要在适应不良状态内发生的作品的概念可视化2情感经验以及从不良适应性的情感经验转变为适应性情感体验的过程。本文中的理论框架建立在艾琳·罗素(Eileen Russell)(2021)的代理,意志和欲望为国家2情感经验的基础上。她提出了这样一个想法:“忽视,剥削和压迫任何形式的发展在自我发展中都留下了漏洞”(第244页),这是Fosha类似地将其描述为未成熟的经历的赤字(Fosha,2013)。我建议,当与不形成自我的客户一起工作时,我们必须在状态2不良适应性影响的领域与患者建立联系;在那里,我们遇到了被忽视的自我的分裂部分,需要被救出。对我的病人来说是正确的,适应不良的情感经历可能只是(目前)的“道路”。没有被认可,见证和感觉到在安全的“其他”面前,分裂的自我不能统一,而真实的自我不能形成和转变。简单地说,患者需要知道自己有一个自我,并且在自己的自我和自我感觉之前对自己有一种感觉。引言本文在处理最深层的依恋创伤时使用AEDP的十年经验,特别是深深忽视的创伤。这种类型的创伤导致一种情感隔离的状态丧失了一种自我,他人的感觉感,并且在世界上作为自己存在。在情感孤立的患者中,尽管患者与自我感疏远,但这种自我确实存在。这个真正的自我属于神经生物学核心自我(Fosha,2013; 2021),但对于亲戚创伤的客户而言,它是无法触及的。这是因为神经生物学核心自我只能在关系安全的背景下访问和感受。
朝向视觉和语言模型辅助对象导航
图3.2布局映射中边界计算过程的可视化。红色圆圈表示代理的位置,而虚线则在探索环境时构成了代理路径的轨迹。蓝色阴影区域代表了从不同位置覆盖的三角形区域。'Frontier X'标记了一个脱落的边界群集的一个示例,展示了观察如何在空间上相关并与地图中的潜在探索目标相关联。。。。。。。。。。9
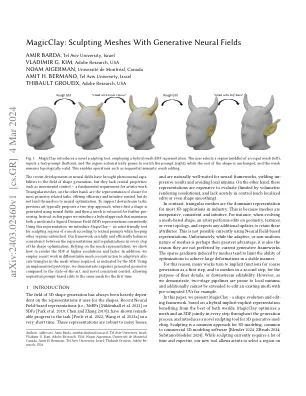
MagicClay:利用生成神经场雕刻网格
神经场领域的最新发展为形状生成领域带来了非凡的能力,但它们缺乏关键特性,例如增量控制——这是艺术创作的基本要求。另一方面,三角形网格是大多数几何相关任务的首选表示形式,它提供了高效且直观的控制,但并不适合神经优化。为了支持下游任务,先前的研究通常提出一种两步法:首先使用神经场生成形状,然后提取网格进行进一步处理。在本文中,我们引入了一种混合方法,该方法能够始终如一地维护网格和有向距离场 (SDF) 的表示形式。基于这种表示形式,我们引入了 MagicClay——一种艺术家友好的工具,可根据文本提示雕刻网格区域,同时保持其他区域不变。我们的框架在形状优化的每个步骤中都仔细有效地平衡了表示形式和正则化之间的一致性;基于网格表示形式,我们展示了如何以更高的分辨率和更快的速度渲染 SDF。此外,我们运用可微分网格重建领域的最新成果,根据 SDF 的指示,在网格中根据需要自适应地分配三角形。通过已实现的原型,我们展示了比现有技术更出色的生成几何体,以及新颖的一致性控制,首次实现了对同一网格进行基于提示的顺序编辑。
加速劳埃德的算法,用于K-均值聚类
摘要K -Means聚类算法是数据挖掘和未加剧的学习的主要内容,之所以受欢迎,是因为它易于实现,快速,易于并行化并提供直观的结果。劳埃德的算法是标准批量的爬山方法,用于最大程度地减少K-均值优化标准。它花费了大部分时间计算k群集中心和n个数据点之间的距离。事实证明,这项工作的大部分是不必要的,因为在第一次迭代之后,点通常会留在同一集群中。在过去的十年中,研究人员开发了许多优化,以加快劳埃德(Lloyd)的算法的低维数据和高维数据。在本章中,我们调查了其中一些优化,并提出了新的优化。特别是我们专注于避免通过三角形不等式计算距离的那些。通过缓存已知距离并用三角形不等式更新它们,这些算法可以避免许多不必要的距离计算。所检查的所有优化产生的结果与劳埃德的算法相同,给定的输入和初始化,因此适用于倒入替换。这些新算法的运行速度比标准未取代的实现更快,并且计算距离要少得多。在我们的实验中,与劳埃德算法相比,通常会看到超过30-50倍的加速度。我们研究了使用这些方法的示例n,dimensions d,簇K和数据结构的权衡。
与阴离子的甲酸下游分离 -
FA初始浓度,[FA] 0的0.05 m和0.50 M. Ambersep 900; [fa] 0 = 0.05 m(黑色圆圈)和0.50 m(红色正方形),琥珀色IRA-96; [fa] 0 = 0.05 m(蓝色钻石)和0.50 m(粉红色星),琥珀石IRA-910; [FA] 0 = 0 = 0.05 m(绿十字)和0.50 m(黄色三角形),固体形状和实线(吸附量),空形和虚线(吸附效率)和mg fa /g r(每克树脂每克甲酸的毫克)。
2025 I级鸟类保护挑战类别
斗篷的尖端由披风的其余部分被笼内水道(也称为斗篷梅运河)隔开。在当地被称为“开普敦岛”,在这里看到的400多种以上的400多种物种中都在这里看到。一个三角形楔形岛,开普敦岛约6平方英里,包含诸如Higbee Beach WMA,Hidden Valley,The Beanery,Nature Conservancy的South Cape May May迁徙鸟类避难所(又名“草地”)和开普人可能指出几个。团队可以在他们选择的情况下漫游该岛。