XiaoMi-AI文件搜索系统
World File Search System用$ D $ - 波磁化的超导体中的磁电效应
简介。在非中心对称超导体[1]中的磁性电源最近引起了极大的关注,尤其是在其在非核心超导反应中的实验应用中[2],例如,如最近的综述[3-6]。特别是,Edelstein磁电效应是由应用超电流引起的自旋极化的产生,而其反场景是二极管效应,即,在两个相反的方向上,临界电流是不同的,在存在外部磁性的情况下会产生的两个相反的方向。这些现象的根本原因之一是违反了由旋转轨道相互作用或不均匀的磁性交换场引起的空间反演象征,该磁性磁性交换场是对能量依赖的动量旋转分裂的作用[7-9],所有这些[7-9]都引起了电子旋转旋转极化之间的耦合和电荷之间的耦合[7]。在本文中,我们考虑了一个具有d-波对称性的共线抗磁性(AFM)订购参数的中心对称金属[11-14]。这种AFM阶诱导了传导费米子的费米表面的特定D波动量依赖性旋转分裂[7-9]。最近在参考文献中审查了各向异性磁顺序的扩展对称分类。[15 - 17]。显示此功能的代表性材料包括,例如,类型AFMS:金属RUO 2,Mn 5 Si 3,VNB 3 S 6,半导体MNTE等[15-20]。此外,最近在thinfms ruo 2中观察到了应变稳定的超导性,tc≈1。[31]。8 K取决于纤维厚度[21-23]。受到最近的实验进展的促进,对超导性的D-波AFM交换耦合的理论研究成为了一个密集的研究领域,包括对Andreev反射的研究和Josephson Current [24-28],在D -Wave Superconcontos in D -Wave Superconcontos ft d -Wave af -Wave afm [29]中的无综合状态[29],或者是30岁的MAD [29],或者有关最近的精彩文章,请参见参考文献。在这种情况下,超导性和磁性的问题自然出现。清楚地,在肌脱肌对称超导体中,与极性超导体中的Edelstein效应相反,诱导的载体的自旋极化与超循环的均匀功能成正比,并表现出D -Wave对称性。
非中心MG10IR19B16
和Pyrochlore超导体CD 2 RE 2 O 7,4 M OS 2 O 6 M = K,RB。5,6也很感兴趣的是基于光元素(例如MGB 2,7 mgcni 3,7 mgcni 3,8 c 6 yb和c 6 Ca,9,9)和第四纪金属间lnni 2 b 2 b 2 C. 10在常规电子 - 磷中的适应性元素中,基于光的元素是相应的元素,该元素是相应的元素。他们显示的频率,建议在寻找新的超导材料时有可行的途径。几乎所有已知的超级导管的一个重要特征是晶体结构中存在反演对称性,这是形成常规库珀对的关键概念。MNSI中缺乏超导性,这归因于其缺乏反转对称性。11,因此,在非中心对称CEPT 3 Si,12 li 2 Pd 3 B,13和Li 2 Pt 3 B Ref的最新报道中,关于超对称Cept 3 Si,12 li 2 pd 3 b。14刺激了在这些化合物中不常见和预测非常规行为的重大努力。15 - 18
EEE 434-591:工程师的量子力学
EEE 434-591:工程师的量子力学 孟涛教授 本课程的内容(包括讲座和其他教学材料)均受版权保护。学生不得在课外分享,包括上传、出售或分发课程内容或在课程进行期间所做的笔记。任何课堂录音仅供参加本课程的学生在参加本课程期间使用。录音和录音摘录不得分发给他人。 课程描述:本课程的目的是加深对量子力学的理解。本课程将简要概述历史,并以波包为例介绍量子力学波函数及其概率解释。课程将介绍薛定谔波动方程,并讨论与现代电子设备相关的解决方案。将特别关注的现象之一是隧道效应,它允许电子“跨越”障碍。本课程还介绍了电子在超小型设备中遇到的电位以及有助于解释氢原子原子轨道的中心对称电位。本课程还将介绍薛定谔波动方程的近似解技术以及微扰理论,这有助于在已知电位受到微小扰动的情况下找到波动方程的解。
χ(3)混合非线性光子学
摘要:光学非线性过程在广泛的应用中是必不可少的,包括超快激光器,显微镜和量子信息技术。在不同的非线性过程中,二阶效应通常不堪重负,除了中心对称系统,二阶易感性在其中消失了,从而允许使用第三阶非线性。在这里,我们演示了一个混合光子平台,可以灵活地调整二阶和三阶敏感性之间的平衡。通过用原子上稀薄的钨化装饰超高的二氧化硅微腔,我们观察到腔体增强的第二谐波产生和汇总频率产生,并以连续波激发的功率水平仅为几百微米。我们表明,可以通过仔细选择二维材料的大小和位置来实现单个设备中二阶和三阶非线性的共存。我们的方法可以推广到其他类型的腔体,从而释放具有对新应用的非线性敏感性的混合系统的潜力。关键字:二维材料,超高Q微腔,第二谐波一代,非线性光学元件,过渡金属二核苷
一种高度兼容 CMOS 的氧化铪基铁电二极管
为了解决“存储墙”问题,人们迫切需要具有高速度和高密度的存储设备。在这里,我们展示了一种高度可扩展的三维可堆叠铁电二极管,其整流极性由 Hf 0.5 Zr 0.5 O 2 薄膜的极化反转调制。通过利用原子分辨率球差校正 STEM 可视化铪/锆晶格序和氧晶格序,我们揭示了 Hf 0.5 Zr 0.5 O 2 薄膜的自发极化与氧原子位移之间的相关性,从而明确地识别出 Hf 0.5 Zr 0.5 O 2 薄膜中的非中心对称 Pca2 1 正交相。我们进一步在 8 层 3D 阵列中实现了这种铁电二极管。演示了高达 20 ns 的运行速度和超过 10 9 的耐用性。超过 100 的内置非线性保证了其自选择特性,从而无需使用外部选择器来抑制大阵列中的漏电流。这项工作为未来存储器层次结构的演进开辟了新的机会。
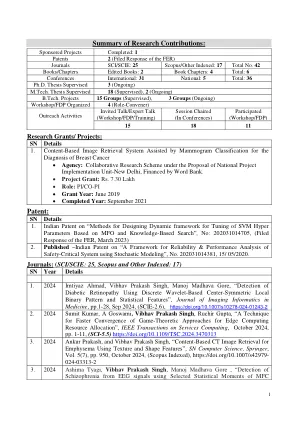
研究贡献摘要:专利:
SN 年份 详情 1. 2024 Imtiyaz Ahmad、Vibhav Prakash Singh、Manoj Madhava Gore,“使用基于离散小波的中心对称局部二值模式和统计特征检测糖尿病视网膜病变”,医学影像信息学杂志,第 1-28 页,2024 年 9 月,(SCIE-2.6),https://doi.org/10.1007/s10278-024-01243-2 2. 2024 Sumit Kumar、A Goswami、Vibhav Prakash Singh、Ruchir Gupta,“一种用于边缘计算资源分配的博弈论方法更快收敛的技术”,IEEE 服务计算学报,2024 年 10 月,第 1-11 页,(SCI-5.5) https://doi.org/10.1109/TSC.2024.3470313 3. 2024 Ankur Prakash 和 Vibhav Prakash Singh,“使用纹理和形状特征进行基于内容的肺气肿 CT 图像检索”,SN Computer Science,Springer,第 5(7) 卷,第 950 页,2024 年 10 月,(Scopus Indexed),https://doi.org/10.1007/s42979-024-03313-2 3. 2024 Ashima Tyagi、Vibhav Prakash Singh、Manoj Madhava Gore,“使用 MFC 的选定统计矩从 EEG 信号中检测精神分裂症
《爱丽丝与鲍勃遇见巴拿赫》勘误表
P. 103,第 4.1 节的注释和备注:我们错误地引用了 [GLMP04] 中的一个结果;它应该是“对于任何中心对称凸体 KĂRn,dBMpK,∆nqďn”。在这种对称性假设和一般性下,这实际上是从练习 4.2 得出的(实际上是一个等式;[GLMP04] 进一步断言,如果其中一个体 K、L 是中心对称的,则 dBMpK,Lqďn)。事实上,KĂ´n∆ 意味着 K 包含在 n∆ 的某个平移中,因此它是∆ 的同位像——比率为 n——关于某个中心(回想一下,通过构造,∆ĂK)。由于 K 的对称中心可能不同于 ∆ 的质心(假设为 0 ),从这个论证中不能立即确定同位体中心的位置。例如,在 [GLMP04] 中引用的例子中心属于 ∆ 的边界,这对于某些应用来说并不理想。如果我们接受任何单纯形(即不一定是体积最大的单纯形),但仍然坚持同位体中心是其质心,则最优因子是什么并不完全清楚。对于不一定对称的体 K °R n ,似乎已知至少在某些情况下,我们可能有 d BM pK, ∆ nq °n 。例如,在 [R. Fleischer, K. Mehlhorn, G. Rote, E. Welzl and C. Yap, Simultaneous inner and outer approximation of shapes. Algorithmica 8 (1992), 365-389] 断言三角形和正五边形之间的距离等于
Piezotronic Algan Nanowire Schottky在金属基板上生长的连接
包括GAN,INN,ALN和ZnO的极性 - 肺导体的非中心对称晶体结构在研究了其菌株诱导的纳米能产生的潜力方面对科学共识感兴趣。耦合的半导体和压电性能产生了一个压电电源,可调节跨其异质结构界面的电荷传输。通过使用导电性原子显微镜,我们研究了在钼(MO)底物上生长的α纳米线(NWS)中产生的压平作效应的机制。通过使用PT – IR探针在NWS/MO结构上施加外部偏置和力,可以调节跨两个相邻的Schottky连接的电荷转运,这是由于明显的Schottky屏障高度(SBHS)的变化,而Schottky屏障高度(SBHS)是由于应变诱导的压电电位而导致的。对于背景力,我们测量了SBH的增加为98.12 MeV,该背景力对应于SBH变化∂ϕ∂F为6.24 MeV/nn,对于半导体/Ti/Mo界面。SBH调制负责对压电效应,通过测量从室温到398 K的温度依赖性I – V曲线进行进一步研究。从Algan NWS/Mo棚的独特结构中获得的见解,这些见解是在Algan/Mo Shed的独特结构上,对Metal-Sendoctor interface的电子特性以及Algan n Nw nw nw nw piquzoe nw pique的电子特性的启发光电子,传感器和能源产生应用。
三路频率分光镜
频域处理在经典和量子光子网络中都具有优势,因为多路复用多个频率的能力允许在多个通道之间高效地传输信息。对于量子信息处理应用,频率自由度已用于定义频率箱量子比特,与空间/偏振量子比特相比,其在损耗方面具有良好的可扩展性 [1]。操纵这些频率箱量子比特需要实现频率模式之间的受控幺正相互作用。最近的进展是开发了由两种频率模式(例如 [2-4])表示的量子比特的频域处理,以及频域三重处理 [5]。实验使用了两种方法:i) 非线性参数过程和 ii) 电光调制。利用参数过程,布拉格散射四波混频 (BS-FWM) 可有效产生高保真量子操作和接近 1 的效率。在这个非线性过程中,两个强泵浦频率模式在两个弱振幅频率模式(信号/闲频)之间引起无噪声频率转换,相当于在布洛赫球上旋转量子比特 [6]。该过程使信号/闲频频率之间的相互作用相位匹配,这些相互作用以零色散频率为中心对称地镜像泵浦频率,如图 1a 所示。由于高阶色散工程,转换过程可以具有频率选择性,从而导致有限的转换效率带宽,如图 1b 所示。尽管双泵 BS-FWM 已经得到充分研究(例如 [4,6,7]),但 N > 2 个泵浦的情况却只得到有限的实验处理 [8]。
DL-丙氨酸重铬酸钾单晶的合成、结构和热研究
摘要 氨基酸及其复合物是一种有机或半有机材料,由于其易于用于光学存储设备而受到广泛关注。DL-丙氨酸是稀有的在非中心对称基团中结晶的氨基酸之一。本文展示了 DL-丙氨酸重铬酸钾 (DAPC) 单晶如何表现出足够的生长。通过单晶 X 射线衍射和粉末 X 射线衍射分析了 DAPC 晶体。利用热重分析/差热分析 (TGA/DTA) 和差示扫描量热法,本文还研究了 DAPC 晶体的熔点、热稳定性、分解点和其他热参数。结果表明,DAPC 的分解点为 397 °C,与 TG/DTA 的分解点相似。还测量了介电常数、耗散和交流电导率,并分析了结果以了解电流操作模型的各种特征。DAPC 单晶的活化能为 0.074 eV。关键词:DAPC,电介质,单晶,热,XRD 引言 有机材料组合在光学生物稳定性和谐波产生 (SHG) 中起着重要作用 [1]。近年来,一些研究人员对其光学特性 (非线性光学) [2] 进行了广泛的研究。同时,氨基酸链在稳定蛋白质结构和催化酶促反应方面起着重要作用,已经发表了许多关于氨基酸(如 L-丙氨酸)的研究文章 [3]。新材料不断被研究,因此,晶体产品的数量多年来不断增加。因此,单晶的发展确保了科学材料的进一步发展。 晶体具有美丽的颜色、闪耀着光芒的光滑表面、清晰的清晰度、具有锋利边缘的多种形状以及透明度(对于某些类型)[4]。水晶传统上被用作装饰品,唤醒了第一批人的审美知识。目前,水晶产品的用途已经从装饰领域扩展到各个科学领域的许多其他实际应用。同时,晶体生长是信息科学与工程的一个重要方面,因为它