XiaoMi-AI文件搜索系统
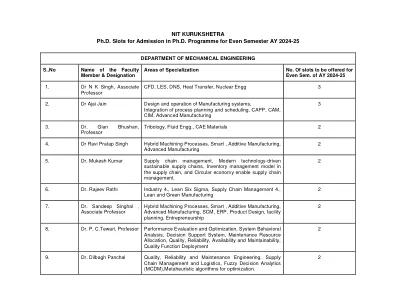
World File Search SystemNIT KURUKSHETRA 博士课程 2024-25 学年偶数学期博士课程招生名额
16. Chhagan 博士,助理教授。认知无线电网络、NOMA 数字通信、微波工程。无线传感器网络、无线通信、MIMO 系统下一代通信系统和物联网。
第一次时隙测试 - 2024 年偶数学期第二次......
学位流 学期 科目代码 科目名称 日期 时间 HU204 环境科学 18-03-24 10:30AM - 11:30AM HU205 印度知识系统 18-03-24 12:15PM - 01:15PM CT201 数据结构 19-03-24 02:15PM - 03:15PM M(CT)201 工程数学 - II 19-03-24 04:00PM - 05:00PM PH(CT)201 工程物理学 21-03-24 10:30AM - 11:30AM EE(CT)201 基础电气与电子工程 21-03-24 12:15PM - 01:15PM HU204 环境科学 18-03-24 10:30AM - 11:30AM HU205 印度知识体系 18-03-24 12:15PM - 01:15PM DS201 数据结构 19-03-24 02:15PM - 03:15PM M(DS)201 离散数学 19-03-24 04:00PM - 05:00PM PH(DS)201 工程物理学 21-03-24 10:30AM - 11:30AM EC(DS)201 基础电气和电子工程 21-03-24 12:15PM - 01:15PM HU201 专业交流 18-03-24 10:30AM - 11:30AM HU202 价值观和道德观 18-03-24 12:15PM - 01:15PM HU203 印度宪法19-03-24 02:15PM - 03:15PM M(EC)201 工程数学 - II 19-03-24 04:00PM - 05:00PM CH(EC)201 工程化学 21-03-24 10:30AM - 11:30AM EC201 电路理论与网络 21-03-24 12:15PM - 01:15PM HU201 专业交流 18-03-24 10:30AM - 11:30AM HU202 价值观与道德观 18-03-24 12:15PM - 01:15PM HU203 印度宪法 19-03-24 02:15PM - 03:15PM M(ECS)201 工程数学 - II 19-03-24 04:00PM - 05:00PM CH(ECS)201 工程化学 21-03-24 10:30AM - 11:30AM ECS201 数据结构与算法 21-03-24 12:15PM - 01:15PM HU201 专业交流 18-03-24 10:30AM - 11:30AM HU202 价值观与道德 18-03-24 12:15PM - 01:15PM HU203 印度宪法 19-03-24 02:15PM - 03:15PM M(EE)201 工程数学 - II 19-03-24 04:00PM - 05:00PM CH(EE)201 工程化学 21-03-24上午 10:30 - 上午 11:30 EE201 电路分析 21-03-24 下午 12:15 - 下午 01:15
具有线性密钥表的偶数-曼苏尔构造和的量子攻击
摘要:Shinagawa 和 Iwata 考虑了 Even–Mansour 和 (SoEM) 构造的量子安全性,并给出了基于 Simon 算法和 Grover 算法的量子密钥恢复攻击。此外,还给出了针对 SoEM 自然泛化的量子密钥恢复攻击。对于 SoEM 的某些变体,他们发现它们的量子攻击并不明显,并将讨论此类构造的安全性作为开放问题。本文重点关注这一开放问题并给出了积极的回应。我们提供了基于量子算法的针对此类构造的量子密钥恢复攻击。对于具有线性密钥调度的 SoEM 自然泛化,我们还给出了基于量子算法(Simon 算法、Grover 算法和 Grover-meet-Simon 算法)的类似量子密钥恢复攻击。
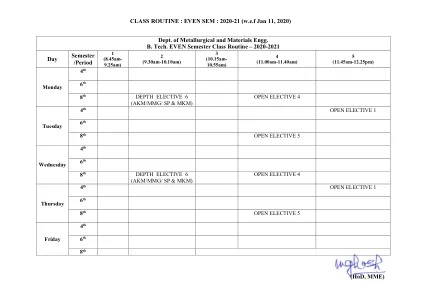
课程安排:偶数学期:2020-21(2020 年 1 月 11 日起)
B.Tech >>> 第 4 学期 第 6 学期 MMC 401:冶金过程中的传输现象 MMC 601:炼钢 MMC 402:相变和相平衡 MMC 602:材料的机械加工 MMC 403:材料特性 深度选修课 1:MME 610:工程材料 CSC 433 MME 616:凝固现象 开放选修课 1 MME 612:炼铁的替代路线 深度选修课 2:MME 617:金属连接工艺 MME 615:陶瓷技术 MME 613:铁合金的生产 第 8 学期 深度选修课 6:MME 813:炼铁和炼钢的原材料准备 MME 811:FEM 建模与仿真材料设计 MME 812:数学建模与仿真 OPEN ELECTIVE 4:MMO 841:材料科学 OPEN ELECTIVE 5 MMG - Madan Mohan Ghosh MKM — MKMondal BM - B. Maji KSG - KS Ghosh DM - D. Mandal SG - S. Ghorai SB - S. Bera BKS - BK Show AKM - AK Mandal JM - J. Maity MM - M. Mallik KPY - KPYagati SP - S. Pramanik
使用原始/对偶数据结构建模和分析 3D 建筑物 ∗
虽然 CityGML 允许我们表示 3D 城市模型,但它在需要空间分析和/或实时修改的应用中的使用受到限制,因为目前存储元素之间拓扑关系的可能性相当有限,而且通常没有得到利用。我们在本文中介绍了一种新的拓扑数据结构,即对偶半边 (DHE),它允许我们表示 3D 建筑物(包括其内部)和周围地形的拓扑。它基于同时存储 3D 空间中的图形及其对偶图并将两者链接起来的想法。我们提出了欧拉型运算符来逐步构建 3D 模型(用于在同时更新对偶结构的同时向模型添加各个边、面和体积),我们还提出了导航运算符来从给定点移动到所有连接的平面或多面体。DHE 还允许我们将属性存储到任何元素。我们已经实施了 DHE,并使用不同的 CityGML 模型对其进行了测试。我们的技术使我们能够处理重要的查询类型,例如在灾害管理规划中查找给定房间最近的外部出口。由于结构是局部可修改的,因此当特定路径不再可用时,模型可能会进行调整。提出的 DHE 结构为日益流行的 CityGML 模型增加了重要的分析价值。
使用原始/对偶数据结构建模和分析 3D 建筑物 ∗
虽然 CityGML 允许我们表示 3D 城市模型,但它在需要空间分析和/或实时修改的应用中的使用受到限制,因为目前存储元素之间拓扑关系的可能性相当有限,而且通常没有得到利用。我们在本文中介绍了一种新的拓扑数据结构,即对偶半边 (DHE),它允许我们表示 3D 建筑物(包括其内部)和周围地形的拓扑。它基于同时存储 3D 空间中的图形及其对偶图并将两者链接起来的想法。我们提出了欧拉型运算符来逐步构建 3D 模型(用于在同时更新对偶结构的同时向模型添加各个边、面和体积),我们还提出了导航运算符来从给定点移动到所有连接的平面或多面体。DHE 还允许我们将属性存储到任何元素。我们已经实施了 DHE,并使用不同的 CityGML 模型对其进行了测试。我们的技术使我们能够处理重要的查询类型,例如在灾害管理规划中查找给定房间最近的外部出口。由于结构是局部可修改的,因此当特定路径不再可用时,模型可能会进行调整。提出的 DHE 结构为日益流行的 CityGML 模型增加了重要的分析价值。