XiaoMi-AI文件搜索系统
World File Search System兰道
信息与热力学：欠阻尼微机械振荡器中兰道尔界限的快速精确方法
信息处理的热力学能量成本是一个被广泛研究的课题，既有其基本方面，也有其潜在的应用[1-9]。该能量成本有一个下限，由 Landauer 原理确定[10]：在温度 T 下，从存储器中擦除一位信息至少需要 k BT ln 2 的功，其中 k B 为玻尔兹曼常数。这是很小的能量，在室温（300 K）下仅为 ∼ 3 × 10 − 21 J，但它是一个通用的下限，与所用存储器的具体类型无关，并且与广义 Jarzynski 等式 [11] 相关。已在多个经典实验中测量了兰道尔边界 (LB)，这些实验使用了光镊 [ 12 ， 13 ]、电路 [ 14 ]、反馈阱 [ 15 – 17 ] 和纳米磁体 [ 18 ， 19 ]，以及捕获超冷离子 [ 20 ] 和分子纳米磁体 [ 21 ] 的量子实验。在准静态擦除协议中可以渐近地达到 LB，其持续时间比上述用作一位存储器的系统的弛豫时间长得多。实际上，当在短时间内执行擦除时，可以使用最优协议最小化此类过程所需的能量，这些协议已经过计算 [ 22 – 27 ] 并用于过阻尼系统 [ 17 ]。更快接近渐近 LB 的另一个策略当然是减少弛豫时间。然而，对于非常快的协议，人们可能想知道机械（电子）系统中的惯性（感应）项是否会影响其可靠性和能量成本。
基于金茨堡 - 兰道和埃利亚斯贝格方程的超导率...
发表的论文，演讲结果：（国际会议的论文）•Kouki Otuka，Shingo Haruna，Yasumasa hasegawa，Hirono Kaneeyasu，“自旋敏感性和野外诱导的非独立超级负责性手性稳定性”，JPS。proc。：第29届低温物理国际会议论文集（LT29）38（1）011058-1-6（2023）。（由国内研究协会等发表的论文等）•iWamoto mutsuo，Isai Kouki，Haruna Shingo，Haruna Shingo，Kaneyasu Hirono，“连接系统中不均匀超导性的磁场引起的磁场引起的历史现象，”，由日本物理学学会提出，”•Haruna Shingo，Ogita Saiki，Nomura Takuji，Kaneyasu Hirono，“通过顶点校正UTE2扰动的超级传导稳定，UTE2中的现场排斥，”，日本物理学学会的收听摘要78（2）（2023）（2023）。（其他）•Koki Doi，Mutsuki Iwamoto，Shingo Haruna，Hirono Kaneeyasu，“超导体交界处的野外诱导的手性状态的滞后”，第10个国际f-召开的国际工场，关于F-Electrons的双重性质（Percter Rectorns off-Electrons tector）。
兰道夫-梅肯今日
认识我的人都知道我是黄夹克运动队的忠实粉丝。今年秋天前所未有的足球胜利带来的兴奋感仍未消退！事实上，我喜欢每年在校内和校外参加数十场黄夹克比赛，目前我正享受着篮球、游泳和男子排球等冬季运动赛季的兴奋。谢丽尔和我为我们的学生运动员加油感到非常自豪，他们占 RMC 学生总数的三分之一以上。我特别欣赏他们是真正的学生运动员，正如旧的 NCAA 电视广告所声称的那样，“他们将在其他运动之外的领域成为职业运动员”。但是等等。别那么快！正如科林·塞尔比 (Colin Selby) '19 所展示的那样，我们以前的黄夹克队确实可以在大舞台上发挥他们的才华！本期的封面故事强调了我们的许多其他校友确实在体育相关职业中取得了成功的未来。它展示了他们如何将在 RMC 磨练出的沟通、领导和决策技能运用到职业体育这一竞争激烈的领域。当然，我们希望所有学生都能利用在 RMC 培养的技能来获得未来的成功。J-Term 假期结束时，超过 150 名大二学生参加了为期两天的强化 Edge 职业训练营。这是我们本学年为整个大二班级举办的第二个此类项目，每个项目都由近 100 名优秀的校友和朋友协助，他们自愿帮助我们的学生学习在不久的将来进入实习和就业市场所需的软技能。这个标志性的项目不仅关注学生在寻求重要的实习机会、最终进入研究生院或第一份研究生工作时最终会做什么，我们还关注帮助他们利用在 RMC 的剩余时间，以提升他们毕业后的前景。如果您是众多认为 RMC 为您的成功做出了贡献的人之一，我希望您能考虑支持我们的 Edge 职业中心，甚至自愿协助学生参加新兵训练营等项目，或特别为他们提供潜在的实习和工作推荐。说到推荐，我们也继续依靠他们来帮助建立我们的入学班级。事实上，我希望您很清楚什么造就了一名优秀的 Randolph-Macon 学生！随着高中毕业生（RMC 2028 届！）和转校生的申请季即将结束，我希望您能与可能考虑来这所大学的学生分享您的经历。并继续分享其他刚刚开始寻找大学的学生（通常是高中二年级和三年级）的姓名 – 我们已经准备好欢迎他们来参观并了解有关 RMC 的更多信息！这个秋天校园里确实很忙碌。希望您喜欢阅读更多有关我们欢呼和庆祝的事情。希望我们很快就能在阿什兰见到您！
哈奇陶黑德-兰道夫综合措施
2022 年 9 月 27 日 — Hatchie Towhead-Randolph 测量（按项目编号标记）。5. 02. 5 5. Needham Rd. O1d. 01e. 9a. 8b. 5a. 3. 8c. 06. 08a. 04a. 公里。8d. 01b.
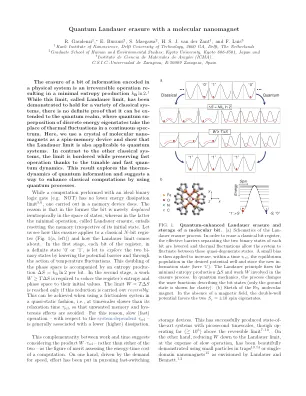
利用分子纳米磁体进行量子兰道尔擦除......
虽然这个极限（称为兰道尔极限）已被证明适用于各种经典系统，但没有确凿的证据证明它可以扩展到量子领域，在量子领域，离散能量本征态的量子叠加取代了连续谱中的热涨落。在这里，我们使用分子纳米磁体晶体作为自旋存储设备，并表明兰道尔极限也适用于量子系统。与其他经典系统相比，由于可调的快速量子动力学，该极限是有边界的，同时还能保持快速操作。这一结果探索了量子信息的热力学，并提出了一种利用量子过程增强经典计算的方法。虽然用理想二元逻辑门（例如 NOT）执行的计算没有最低能量耗散限值 5,6，但在存储设备中执行的计算却有。原因在于，在前者中，位仅仅是在状态空间中等熵地移动，而在后者中，最小操作（称为兰道尔擦除）需要重置存储器，而不管其初始状态如何。让我们看看这种擦除如何应用于经典的 N 位寄存器（图 1(a，左)）以及兰道尔极限是如何产生的。在第一阶段，寄存器的每一位都处于确定的状态“0”或“1”，通过降低势垒和通过温度波动的作用来探索两个二进制状态。相空间的这种加倍伴随着每位的熵产生∆S=kBln2。在第二阶段，需要做功 W ≥ T∆S 来将寄存器的熵和相空间减少到它们的初始值。只有当这种减少以可逆的方式进行时，才能达到极限 W=T∆S。这可以通过使用准静态无摩擦系统来实现，即在比其弛豫时间 τ rel 更慢的时间尺度上，从而避免不必要的记忆和滞后效应。因此，相对于系统相关的 τ rel ，慢速（快速）操作通常与较低（较高）的耗散相关。