机构名称:
¥ 1.0
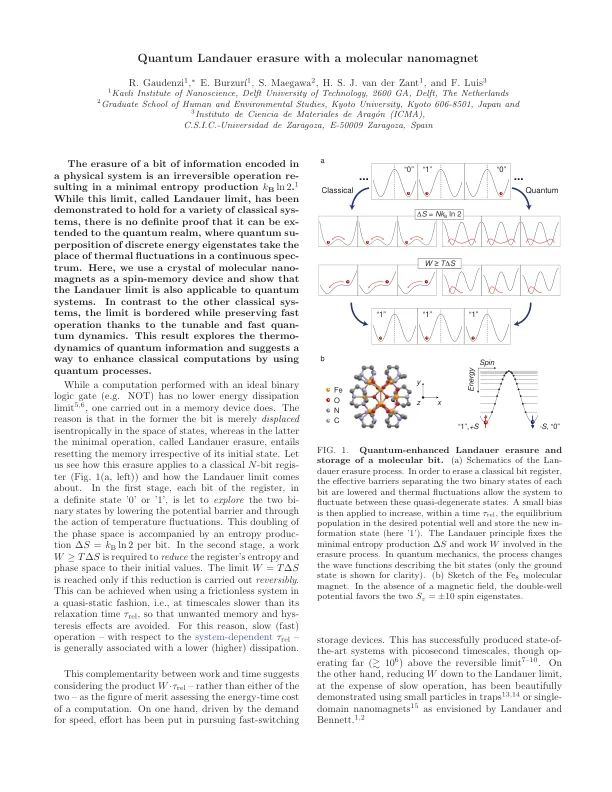
虽然这个极限(称为兰道尔极限)已被证明适用于各种经典系统,但没有确凿的证据证明它可以扩展到量子领域,在量子领域,离散能量本征态的量子叠加取代了连续谱中的热涨落。在这里,我们使用分子纳米磁体晶体作为自旋存储设备,并表明兰道尔极限也适用于量子系统。与其他经典系统相比,由于可调的快速量子动力学,该极限是有边界的,同时还能保持快速操作。这一结果探索了量子信息的热力学,并提出了一种利用量子过程增强经典计算的方法。虽然用理想二元逻辑门(例如 NOT)执行的计算没有最低能量耗散限值 5,6,但在存储设备中执行的计算却有。原因在于,在前者中,位仅仅是在状态空间中等熵地移动,而在后者中,最小操作(称为兰道尔擦除)需要重置存储器,而不管其初始状态如何。让我们看看这种擦除如何应用于经典的 N 位寄存器(图 1(a,左))以及兰道尔极限是如何产生的。在第一阶段,寄存器的每一位都处于确定的状态“0”或“1”,通过降低势垒和通过温度波动的作用来探索两个二进制状态。相空间的这种加倍伴随着每位的熵产生∆S=kBln2。在第二阶段,需要做功 W ≥ T∆S 来将寄存器的熵和相空间减少到它们的初始值。只有当这种减少以可逆的方式进行时,才能达到极限 W=T∆S。这可以通过使用准静态无摩擦系统来实现,即在比其弛豫时间 τ rel 更慢的时间尺度上,从而避免不必要的记忆和滞后效应。因此,相对于系统相关的 τ rel ,慢速(快速)操作通常与较低(较高)的耗散相关。
利用分子纳米磁体进行量子兰道尔擦除......
主要关键词