XiaoMi-AI文件搜索系统
World File Search System讲义
4 量化量子信息和量子无知 72 4.1 冯诺依曼熵。。。。。。。。。。。。。。。。。。。。。。。。。。。72 4.2 量子相对熵。。。。。。。。。。。。。。。。。。。。。。。。。76 4.3 净化,第 1 部分。。。。。。。。。。。。。。。。。。。。。。。。。。。。。78 4.4 舒马赫压缩。。。。。。。。。。。。。。。。。。。。。。。。。。80 4.5 量子通道。。。。。。。。。。。。。。。。。。。。。。。。。。。。。82 4.6 通道二元性 .。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。89 4.7 净化,第 2 部分。。。。。。。。。。。。。。。。。。。。。。。。。。。。。94 4.8 深度事实 ..................................100 4.9 条件熵的操作意义 ..........。。112
OCR GCSE 计算机科学 (J277) 修订指南
计算机架构 这是计算机硬件的内部逻辑结构和组织。它说明了计算机的各个不同部分如何组合在一起并有效地协同工作 冯·诺依曼架构 冯·诺依曼架构解释了所有设备在处理信息时如何遵循一般规则。所有数据和程序都存储在计算机内存中,并以二进制数字(0 和 1)的形式存储。 输入 — 数据通过输入设备(如键盘、鼠标、麦克风等)输入到设备中 CPU — 数据由 CPU 通过控制单元和 ALU 处理 内存单元 — 数据在 CPU 和计算机内存之间传输 输出 — 最后,经过处理后,数据通过输出设备(如显示器、扬声器、打印机等)输出给用户 输入设备 我们用来将信息发送到计算机的设备,例如鼠标、键盘、麦克风等 输出设备 我们用来将信息从计算机中发送出去的设备,例如显示器、扬声器、打印机等 CPU(中央处理单元) 这是计算机的大脑。它使用提取、解码、执行周期 Hz (赫兹) 来处理用户提供的所有指令。这是我们测量 CPU 速度的标准。1Hz = 每秒可执行 1 条指令。CPU 的常见速度现在以兆赫 (MHz) 或千兆赫 (Ghz) 为单位
我的神经网络是神经形态的吗?神经形态工程的分类、最新趋势和未来方向
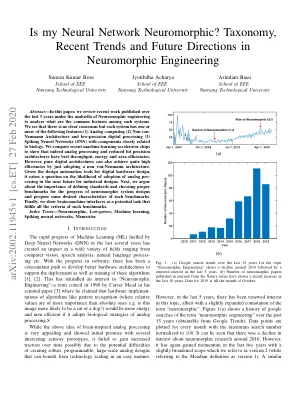
摘要 — 在本文中,我们回顾了过去 3 年在神经形态工程领域发表的最新研究,以分析此类系统的共同特征。我们发现没有明确的共识,但每个系统都具有以下一个或多个特征:(1)模拟计算(2)非冯诺依曼架构和低精度数字处理(3)脉冲神经网络 (SNN),其组件与生物学密切相关。我们比较了最近的机器学习加速器芯片,以表明模拟处理和降低位精度的架构确实具有最佳的吞吐量、能量和面积效率。然而,纯数字架构也可以通过采用非冯诺依曼架构来实现相当高的效率。鉴于数字硬件设计的设计自动化工具,它提出了一个问题,即在不久的将来工业设计中采用模拟处理的可能性。接下来,我们讨论了定义标准和选择适当基准对于神经形态系统设计进展的重要性,并提出了此类基准的一些期望特征。最后,我们展示了脑机接口作为一项潜在任务,它满足了这些基准的所有标准。索引术语——神经形态、低功耗、机器学习、脉冲神经网络、忆阻器
基于离散和连续吸引子网络的神经形态系统基于忆阻器的生物可信记忆
正是对建立一整套新的数学工具以分析和评估未来神经形态计算系统的启发。忆阻器于1971年被提出[4],并于2008年通过实验建立[5],它是一种电阻性器件,是针对这种非冯·诺依曼计算优化的未来神经形态器件。忆阻器可以根据内部状态和外部刺激(如电压脉冲)改变其电阻。先前的研究表明,基于忆阻器的交叉结构可以依靠欧姆定律和基尔霍夫定律,将计算最密集的组件矢量矩阵乘法(VMM)直接映射到电参数,从而加速各种人工神经网络(ANN)。[6,7]在此原理下,VMM计算过程直接在原位进行,从而避免了因从内存中获取数据而导致的内存墙(冯·诺依曼瓶颈)。尤其是在监督学习中,它可以降低前馈过程和从 NP 到 P 的反向传播的计算复杂度。[8] 因此,当前的研究主要集中在分类和回归任务上,以利用这种新的计算机制作为互补金属氧化物半导体 (CMOS) 电路的补充。然而,忆阻器的不同物理机制,如导电丝的形成/溶解和相变,决定了器件存在需要进一步优化的缺陷。[9,10]
实验室介绍 电气工程学院
[深度学习和神经网络处理器设计] 深度学习算法最近受到了极大的关注。GPU 被广泛用于运行神经网络,但由于其能效低,不适合集成到智能手机、可穿戴设备和无人机等移动设备中。我们专注于高性能和节能的专用神经网络处理器的设计和实现。为此,我们正在研究针对神经网络优化的数据路径和内存架构、处理各种神经网络模型的灵活硬件架构以及硬件友好的神经网络算法。最后,基于我们的想法设计、制造和测试了神经网络处理器芯片。我们正在最受认可的会议上进行最先进的研究。[深度学习的内存处理] 传统的冯诺依曼架构在处理以内存为主的深度学习算法时严重受到内存瓶颈问题的困扰,因为大量数据必须通过窄总线从主内存传输到处理器。同时,遵循非冯·诺依曼架构的内存处理(PIM)技术将数据处理在内存中,只将必要的数据传输到处理器,降低了内存传输的能耗成本。因此,内存处理范式是高效处理大规模深度神经网络的重点方向和下一代平台。
流程图、断言和形式化方法? - Mark Priestley
流程图是现代计算的标志性可视化表示之一。1947 年,赫尔曼·戈德斯坦和约翰·冯·诺依曼发明了流程图,作为他们所谓的“问题规划和编码”综合方法的一部分。在接下来的至少 20 年里,流程图成为了计算机程序开发的随处可见的辅助工具。人们使用了各种各样的符号,但所有形式的流程图都包含表示操作和决策点的方框,并由表示控制流的有向线段连接起来 [18]。尽管流程图无处不在,但历史学家对其作用仍心存质疑。人们批评流程图不是开发过程的重要组成部分,反而认为它是繁琐且具有误导性的文档,只是在官僚主义项目经理的要求下制作。Ensmenger [5] 将其描述为边界对象,其价值在于它们能够在管理人员和开发人员之间进行调解,但对这两组人而言,它们的含义不同。鉴于此,我们惊讶地发现,对于戈德斯坦和冯·诺依曼来说,流程图不仅提供了程序结构的图形表示,而且还提供了复杂的数学符号。他们定义了许多形式条件,类似于我们现在所说的证明规则,用于证明图表的一致性。将原始图表描述为设计符号而不是定义软件开发形式化方法的早期尝试并非不合理,尽管有点不合时宜。
佩奇曲线和线性光学中的典型纠缠
玻色子高斯态是无限维希尔伯特空间中一类特殊的量子态,与通用连续变量量子计算以及近期的量子采样任务(如高斯玻色子采样)相关。在这项工作中,我们研究了由随机线性光学单元演化的一组压缩模式中的纠缠。我们首先推导出 R´enyi-2 Page 曲线(纯玻色子高斯态子系统的平均 R´enyi-2 熵)和相应的 Page 校正(子系统的平均信息)在某些压缩状态下的模式数渐近精确的公式。然后,我们通过研究其方差,证明了用 R´enyi-2 熵测量的纠缠典型性的各种结果。利用上述 R´enyi-2 熵的结果,我们确定了冯·诺依曼熵佩奇曲线的上限和下限,并证明了以冯·诺依曼熵为衡量标准的某些纠缠典型性状态。我们的主要证明利用了熵的平均值和方差所遵循的对称性,这大大简化了对幺正函数的求平均。鉴于此,我们提出了未来可能利用这种对称性的研究方向。最后,我们讨论了我们的结果及其在高斯玻色子采样中的推广以及阐明纠缠和计算复杂性之间的关系的潜在应用。
QLA 与 QIT II 相遇海报 - 普渡大学数学
几十年来,各种数学家、计算机科学家、物理学家和工程师在定量线性代数 (QLA) 和量子信息理论 (QIT) 之间建立了惊人的联系和联系。定量线性代数位于差异理论、谱图理论、随机矩阵、几何群论、遍历理论和冯·诺依曼代数等主题的交叉点。特别是,特别强调了无限维分析中出现的问题与有限维中定量出现的问题之间的联系。