XiaoMi-AI文件搜索系统
World File Search System双曲图扩散模型
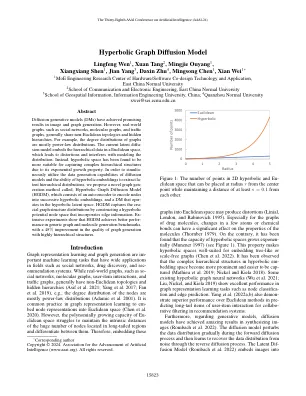
扩散生成模型(DMS)在图像和图生成方面取得了有希望的结果。然而,现实世界图,例如社交网络,分子图和交通图,通常共享非欧国人拓扑和隐藏的层次结构。例如,图的度分布主要是幂律分布。当前的潜在扩散模型将层次数据嵌入到欧几里得空间中,从而导致扭曲并干扰建模分布。取而代之的是,由于其指数生长特性,已发现双曲线空间更适合捕获复杂的层次结构。In order to simulta- neously utilize the data generation capabilities of diffusion models and the ability of hyperbolic embeddings to extract la- tent hierarchical distributions, we propose a novel graph gen- eration method called, Hyperbolic Graph Diffusion Model (HGDM), which consists of an auto-encoder to encode nodes into successive hyperbolic embeddings, and a DM that oper- ates in the双曲线潜在空间。HGDM通过构造包含边缘信息的双曲线潜在节点空间来捕获Crucial图结构分布。的实验实验表明,HGDM在通用图和分子生成基准测试中获得了更好的表现,并且具有高度层次结构的图生成质量提高了48%。
双曲格子:- CORE
0.1 最小重量 为了生存,大自然学会了用最少的物质资源生产出极其高效的结构。在这种情况下,效率是对生物体的结构、形式和目的之间相互依存关系的发达认识。对最小重量的需求因生物体的功能和环境而异。空中结构出于需要,已将其结构系统的重量降至最低;相比之下,水生生物仅受重力的影响很小。例如,鲸鱼比任何陆地动物都大得多,它之所以能达到这个大小,只是因为它的身体密度与周围的海水介质相似。一旦在陆地上受到全部重力,鲸鱼就有因自身重量而倒下的危险。在自然界中,有一件事是肯定的,那就是只要重量可以最小化,它就会对新陈代谢有利。
大脑可以表示为双曲几何吗?
具有 3-D 双曲空间 H 3 。当 h eff = nh 0 时,任何携带暗物质的系统的磁体 (MB) 都提供了任何系统的表示(反之亦然)。MB 能否提供这种表示,作为因果菱形 (cd) 的 3-D 双曲面的镶嵌,定义为 M 4 的未来和过去定向光锥的交点?由 SL (2, Z) 的子群或其用代数整数替换 Z 的泛化标记的镶嵌点将由其统计特性决定。H 3 处神经元磁像的位置将定义 H 3 的镶嵌。镶嵌可以映射到庞加莱盘的模拟 - 庞加莱球 - 表示为未来光锥的 t = T 快照(t 是线性闵可夫斯基时间)。t = T 之后,神经元系统的大小不会改变。镶嵌可以将认知表征定义为一组离散的时空点,其坐标为可分配给表示 MB 的时空表面的有理数的某种扩展。有人可能会认为 MB 具有更自然的圆柱对称性而不是球对称性,因此也可以考虑在 E 1 × H 2 处使用圆柱表示
Huanyu Qu曲环宇博士学位:yc37960@umac.mo
! 您的F,Wu Y,Ma S,Xu M,Li H,Qu H等。 脑启发的多模式杂交神经您的F,Wu Y,Ma S,Xu M,Li H,Qu H等。 脑启发的多模式杂交神经脑启发的多模式杂交神经
DNA双链断裂修复途径的选择与调控
图 1 DSB 修复途径总览 .DSB 发生后 , Ku70-80 会最先结合上来 , 如果不发生末端切除 , 会继而招募 DNA-PKcs, ligase IV, XRCC4 等 cNHEJ 核心因子介导 cHNEJ 修复途径 .如果末端发生 MRN-CtIP 介导的末端切除 , 则会产生 ssDNA 抑制 cNHEJ 修复途 径 .短程切除和长程切除产生的 ssDNA 可以通过链内退火进行修复 , 分别被称为 alt-EJ 和 SSA.长距离切除产生的 ssDNA 也可以 在 BRCA2-PALB2-BRCA1 复合体的帮助下和 RAD51 形成核蛋白纤维 , 进行同源找寻和连入侵过程 , 从而进入 HR 修复途径 .HR 途径又可以分为 BIR, SDSA 和 DSBR Figure 1 Overview of DSB repair pathways.The broken ends are first recognized and bound by Ku70-80.Without end resection, other cNHEJ core factors, such as DNA-PKcs, ligase IV, XRCC4, would be recruited to DSBs to mediate cNHEJ pathway.When MRN-CtIP-mediated resection occurs, the generated ssDNA will inhibit cNHEJ pathway.ssDNA from short-range and long-range resection can anneal in-strand to resolve the damages, termed Alt-EJ and SSA, respectively.ssDNA from long-range resection can also be bound by RAD51 to form nucleoprotein filament under the help of BRCA2-PALB2-BRCA1 complex.Nucleoprotein filament carry out homologous searching and strand invasion, promoting HR pathway.The HR pathway could be divided into BIR, SDSA and DSBR
基于ROS的双机械臂协同感知抓取系统设计与实现
机器人手臂任务中的感知技术。通过分析机器人臂的运动学并设计双臂合作系统,将视觉点云技术结合起来,实现双臂合作握把,并通过使用ROS平台来验证合作社CON-TROL策略的有效性,从而构建双臂臂系统的实验平台。主要研究内容包括分析机器人ARM运动学的正和反向运动学模型,视觉点云识别在双臂合作任务中的应用,双臂合作控制策略的实现以及合作掌握的实验结果和分析。通过这项研究,成功设计和实现了基于ROS的双机器人臂合作感,并实现了双臂合作控制策略的有效性。
分数薛定谔方程中双曲双阱势的量子信息熵
摘要:在本研究中,我们研究了双曲双阱势 (HDWP) 的分数阶薛定谔方程 (FSE) 中的位置和动量香农熵,分别表示为 S x 和 S p 。我们在分析中探索了用 k 表示的分数阶导数的各种值。我们的研究结果揭示了有关低位态的位置熵密度 ρ s ( x ) 和动量熵密度 ρ s ( p ) 的局部化特性的有趣行为。具体而言,随着分数阶导数 k 的减小,ρ s ( x ) 变得更加局部化,而 ρ s ( p ) 变得更加非局部化。此外,我们观察到随着导数 k 的减小,位置熵 S x 减小,而动量熵 S p 增加。特别地,这些熵的总和随着分数阶导数 k 的减小而持续增加。值得注意的是,尽管随着 HDWP 深度 u 的增加,位置 Shannon 熵 S x 增加,动量 Shannon 熵 S p 减少,但 Beckner–Bialynicki-Birula–Mycielski (BBM) 不等式关系仍然成立。此外,我们研究了 Fisher 熵及其对 HDWP 深度 u 和分数阶导数 k 的依赖关系。结果表明,Fisher 熵随着 HDWP 深度 u 的增加和分数阶导数 k 的减小而增加。
双曲矩阵分解可提高药物预测
过去,计算系统生物学的研究更多地侧重于高级统计和数值优化技术的开发和应用,而较少关注对生物空间几何形状的理解。通过将生物实体表示为低维欧几里得空间中的点,最先进的药物-靶标相互作用 (DTI) 预测方法隐含地假设生物空间具有平坦的几何形状。相比之下,最近的理论研究表明,生物系统表现出具有高度聚类性的树状拓扑结构。因此,将生物系统嵌入平坦空间会导致生物对象之间距离的扭曲。在这里,我们提出了一种用于药物-靶标相互作用预测的新型矩阵分解方法,该方法使用双曲空间作为潜在生物空间。与经典的欧几里得方法相比,双曲矩阵分解表现出卓越的准确性,同时将嵌入维度降低了一个数量级。我们认为这是双曲几何支撑大型生物网络的额外证据。
2024 Xiamen Darius Catalog-双页印刷版(无嵌入)修改尺寸 ...
达里乌斯(Div> Darius)一直专注于全球智能保健产品的制造已有10多年的历史,并积累了超过1000万单位的保健产品。目前,该公司有16个§ĉĉáì¶çĭ。 Öîtouminstrecoustout。
PT对称双曲结构中电磁波的传播
在PT-对称周期性堆栈中电磁波的传播由介电介质分离,这些叠层由具有平衡损耗和增益的介电培养基分隔。确定了pt-对称半导体 - 电介电量堆栈的特征性分散性能的特征频率。考虑了层的损耗/增益水平和层厚度对带谱的演变的影响。在这里我们表明,有效的培养基方法无法充分描述PT-对称超晶体中的传播波。证明了PT-对称双曲系统中各向异性传递共振的存在和高度反射。检查了结构参数和入射角对散射基质的PT-对称性跃迁的影响。