XiaoMi-AI文件搜索系统
World File Search System反对称
SPIE 会议纪要
进行风洞试验，测量亚音速流中圆柱体上半球转塔的非稳定表面压力场。这些测量值是使用与快速响应压敏涂料耦合的压力传感器获得的。分析了 0.5 马赫流动（Re D ≈ 2 × 10 6 ）在三种不同转塔突出距离下产生的表面压力场数据。之前，使用适当的正交分解发现了转塔上的主要表面压力模式。结果表明，转塔向自由流的突出程度越大，展向反对称表面压力场波动的发生率就越高。这些反对称压力波动是由反对称涡脱落引起的。然而，当使用部分浸没的半球形转塔几何形状时，结果表明这种反对称模式的相对能量要低得多。这表明，随着突出物从部分浸没变为全半球配置，流场现象会发生转变。对这种所谓的“模式切换”的进一步研究是本文介绍的工作重点。这项研究主要依赖模态分析来确定炮塔和尾流表面压力场之间的相关性。研究发现，部分半球周围的表面压力场波动主要受尾流影响，而炮塔本身的流体结构影响很小。对于半球和半球对圆柱的配置，对称和反对称非稳定分离成为最大的影响，并与尾流波动相结合。
JHEP02(2025)008
摘要：在混沌多体系统中，涉及一般非守恒局部算子的 OTOC 的后期行为呈现指数衰减。然而，最近观察到，对于某些全息理论，涉及规范场的 U (1) 守恒电流的 OTOC 在后期反而会呈扩散变化。本研究将这一观察结果推广到对应于更高形式对称性的守恒电流，这些对称性属于更广泛的对称类，称为广义对称性。我们首先计算了五维 AdS-Schwarzschild 黑洞几何中 2 形式反对称 B 场的涉及 U (1) 电流算子的 OTOC 的后期行为。B 场的体解在渐近 AdS 边界附近表现出对数发散，可以通过在边界 CFT 中引入双迹变形来正则化。最后，我们考虑任意维度中反对称 p 形式场的更一般情况。在散射方法中，边界 OTOC 可以写成渐近“入”和“出”状态之间的内积，在我们的例子中，这相当于计算具有和不具有冲击波背景的两个体场之间的内积。我们观察到后期 OTOC 具有幂律尾部，这似乎是具有 U (1) 电荷守恒的高阶形式场的普遍特征。
补充材料“可控的奇数库珀对在多杀手约瑟夫森连接处”
因此，可以通过执行各个量子数交换的所有可能组合来获得允许的对振幅（eqs。（S2）和（S3）），填充反对称条件等式。（S1）。这样做，我们发现八个允许尊重反对称条件的对对称类别，其中4对应于奇数相关性，请参见表S1。特定相关性是超导索引（sup。索引）在扩大允许的对对称性方面起着至关重要的作用。表S1在主文本的“ jjs中的us频间振幅”部分中显示为表1。在没有任何自旋粘合字段的情况下，出现对的相关性的自旋对称性与母体超导体的自旋对称性相同。因此，在我们的研究中允许的对对称类别（不存在旋转式粘合字段）是ESEE和OSOE对对称类别：它们对应于超导体指数中的偶数（奇数频率）旋转（奇数）均匀（奇数）旋转单元（奇数），甚至对应于超导器指数。通过包括一个自旋混合字段，可以获得表S1中对应于OTEE和OTOO对对称类别的奇数自旋 - 三个三角对振幅，可以用作超导阶段高度可控制的旋转源，从而可以使超导性旋转旋转的超导量。由于我们在主文本中提出的结果中没有自旋混合字段，因此其中的对对称性表现出父母超导体的自旋对称性，即自旋单旋。这是在主文本的“ JJS中的persupconductor对振幅”部分中特别讨论的。
货仓对飞机结构的影响 - NATO STO
需要一个有限元模型，该模型将使用地面和飞行测试结果进行更新。分析研究的基础可以是粗网格模型，该模型由精细有限元组件模型派生而来，组装成完整的飞机模型。使用细静态网格模型作为基本模型的优点是，在细化的情况下，可以一步更新所有使用的模型。从选定的假设模式中，将计算一组广义非定常气动矩阵。为了分析真实情况，研究了不同表面的气动干扰。通过低速风洞试验和飞行试验验证了分析计算。主要飞行试验是颤振、结构耦合以及振动和载荷调查。在对称或反对称情况下，使用不同的激励方法和机动来激励飞机。
半导体芯片中的工程两次波函数和交换统计数据
高维纠缠的光状态为量子信息提供了新的可能性，从量子力学的基本测试到增强的计算和通信效果。在这种情况下，自由度的频率将鲁棒性的资产结合在一起，并通过标准的电信组件轻松处理。在这里，我们使用集成的半导体芯片来设计直接在生成阶段的频率键入光子对的波函数和交换统计，而无需操作后。量身定制泵束的空间特性，可以产生频率与年轻相关，相关和分离状态，并控制光谱波函数的对称性，以诱导骨气或费米子行为。这些结果是在室温和电信波长下获得的，开放有希望的观点，用于在整体平台上使用光子和光子的量子模拟，以及利用反对称高度高维量子状态的通信和计算方案。
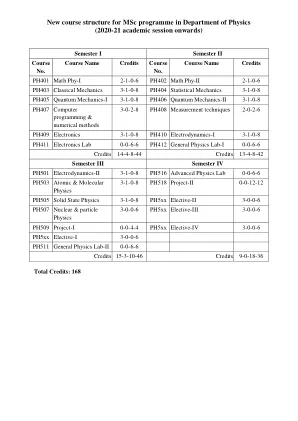
物理系理学硕士课程的新课程结构
PH401：数学物理 I (2-1-0-6) 线性代数：线性向量空间：对偶空间和向量、柯西-施瓦茨不等式、实数和复数向量空间的定义、度量空间、线性算子、子空间；跨度和线性独立性：行减少和方法；基础和维度：使用简化的跨度和独立性测试 (RREF) 方法；线性变换：图像、核、秩、基础变换、转移矩阵、同构、相似变换、正交性、Gram-Schmidt 程序、特征值和特征向量、希尔伯特空间]。张量：内积和外积、收缩、对称和反对称张量、度量张量、协变和逆变导数。常微分方程和偏微分方程：幂级数解、Frobenius 方法、Sturm-Liouville 理论和边界值问题、格林函数；笛卡尔和曲线坐标系中不同波动方程的分离变量法，涉及勒让德、埃尔米特、拉盖尔和贝塞尔函数等特殊函数以及涉及格林函数的方法及其应用。教材：
博士课程的教学大纲
1。数学物理学（信用：3，约25小时）Phys04-001-C线性向量空间，线性操作员和矩阵，线性方程系统。特征值和特征向量。张量：引言和定义，对称和反对称张量，笛卡尔和非笛卡尔张量和协变量导数，基督教符号，不可减至表示，直接产物和收缩，牛顿力学和相对论中的张量。线性普通微分方程，物理学中的线性偏微分方程，绿色功能，变量解决方案方法的分离，特殊功能及其在物理学中的应用。复杂的变量理论；分析功能。Taylor和Laurent扩展，分析延续，轮廓整合，分散关系。积分方程：Fredholm和Volterra方程，微分方程向积分方程的转换，求解积分方程的方法。有限和连续群体简介。小组表示和操作，置换组及其表示群体。建议的书：
![arxiv：2010.09104v1 [Quant-ph] 2020年10月18日](/simg/g:\will\search\icon\source\e\e846a411b40da8e2c0bce1165504267dea38f95a.webp)
arxiv：2010.09104v1 [Quant-ph] 2020年10月18日
在晶格上的量子行走可以在长波长极限下引起单粒子相对论波方程。进入多个颗粒时，量子细胞自动机（QCA）是量子步行的天然概括。在一个空间维度中，可以将量子行走“促进”到QCA，该QCA在长波长的极限中会导致非互动费米子的dirac量子界面理论（QFT）。此QCA/QFT对应关系具有理论和实际应用，但是在两个或多个空间维度中，类似结构存在障碍。在这里，我们表明，采用与完全反对称子空间配置的可区分颗粒的构造方法在两个空间维度中产生QCA，从而导致2D Dirac QFT。对3D的概括将带来一些其他并发症，但没有概念上的障碍。我们研究了这种构建如何逃避“不走”，从而导致早期工作。
2412.08694v1.pdf
量子密钥分发 (QKD) 提供了一种理论上安全的密钥共享方法，但实际实施面临长距离信道噪声和损失带来的挑战。传统的 QKD 协议需要大量的噪声补偿，这阻碍了其工业可扩展性并降低了可实现的密钥速率。替代协议在抗噪声状态下对逻辑量子位进行编码，但代价是使用许多物理量子位，增加了丢失的可能性并限制了传输距离。在这项工作中，我们引入了一种逻辑量子位编码，它在连续光子自由度、频率和时间中使用反对称贝尔态。通过利用连续空间，我们通过最小化每个逻辑量子位的光子数量来克服这种噪声损失稳健性权衡，同时优化编码对噪声波动的弹性。我们分析了我们的编码的安全性，并证明了它与现有的最先进协议相比的稳健性。这种方法为在现实噪声条件下实现可扩展、高效的 QKD 实施提供了一条途径。