XiaoMi-AI文件搜索系统
World File Search System和量
机器学习和量子计算简介
2 前馈神经网络 7 2.1 梯度下降. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 2.2 Colab、Python、Tensorflow、Keras 和 Pytorch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2.3.2 非线性激活 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... 15 2.6.1 训练. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
su中的金属绝缘体过渡和量子磁力（3 ...
3插入，用三个可能的自旋弹道在平均每个位置一个粒子的平均晶格上进行建模。我们提供了一个量子临界点的明确证据，将非磁性均匀金属相与存在长期“自旋”顺序的制度分开。通过不同的摩avors的规则，远程交替的多个连续过渡到磁性状态，随着相互作用强度的提高，其对称性会变化，显着地扩展了海森堡限制到巡回效率的先前工作。除了丰富的量子磁性外，与通常的SU（2）模型相比，这种重要的物理系统还允许研究整数填充和相关的Mott过渡，从而脱离了嵌套的距离。我们的结果还为解释当前和未来的实验提供了关于费米金碱 - 地球原子以及SU（N）物理学的其他实现的重要一步。
单分子分辨率下的直接翻转动力学和量化手性的富集
手性是自然的重要方面，并且已经开发出许多宏观方法来了解和控制手性。对于手性高等胺，它们的柔性翻转过程使得在不形成粘结和破裂的情况下实现高性能可控性。在这里，我们提出了使用石墨烯 - 分子 - 透明烯单分子连接的第三级胺形成的一种稳定的手性单分子器件。这些单分子设备允许实时，原位，并长期测量具有高时间分辨率的个体手性氮中心的翻转过程。温度和偏置电压依赖性实验以及理论研究表明多种性手性中间体，表明通过能量相关因素对翻转动力学进行调节。角度依赖性测量进一步证明了使用与对称相关因子线性极化的光线有效地富集了手性态。这种方法提供了一种可靠的手段，可以理解手性的起源，阐明微观手性调节机制，并有助于有效药物的设计。
使用经典和量子机学习模型的洪水预测
这项研究研究了量子机学习的潜力（QML）改善洪水预测。我们专注于2023年德国武河沿线的每日洪水事件。我们的方法将经典的机器学习（SVM，KNN，回归，AR模型）与QML技术（adaboost，量子变异电路，Qboost，qsv c _ ml）结合在一起。该混合模型利用量子和纠缠等量子特性，以提高准确性和效率。经典模型和QML模型。结果表明，QML模型的竞争训练时间和提高了预测准确性。这项研究意味着朝着利用量子技术进行变化适应的一步。我们强调合作和持续创新，以在现实世界中实施这种模型，最终增强了针对洪水的全球弹性。
保护法和量子力学的基础
在最近的一篇论文中，[y。 Aharonov，S。Popescu，D。Rohrlich，Proc。natl。学院。SCI。 U.S.A. 118 E1921529118（2021）]，但据认为，尽管量子力学中保护法的标准定义是具有统计特征的量子力学，但它是完全有效的，但它却错过了自然的基本特征，并且必须重新研究以解决在各个情况下的保护/非保护问题的问题。 特别是在上文中提出了一个实验，可以证明在某些个体情况下，尽管统计保守，但不能保守能量。 然而，人们认为这很令人担忧，并且如果在某些情况下不坚持，即使标准保护法不需要保护，也必须出错。 在这里，我们重新访问了该实验，并表明尽管结果是正确的，但有一种方法可以规避它们并确保在这种情况下进行单个案例保护。 该解决方案是非常不寻常的，挑战了量子力学的基本假设之一，即可以准备任何量子状态，并且涉及时期的，双重的非保守效应。 我们的结果阐明了粒子初始状态的制备阶段的作用以及保护定律和参考框架的相互作用。 我们还推测，当对任何保护实验进行这样的完整分析时，在每种情况下都会遵守保护。SCI。U.S.A. 118 E1921529118（2021）]，但据认为，尽管量子力学中保护法的标准定义是具有统计特征的量子力学，但它是完全有效的，但它却错过了自然的基本特征，并且必须重新研究以解决在各个情况下的保护/非保护问题的问题。特别是在上文中提出了一个实验，可以证明在某些个体情况下，尽管统计保守，但不能保守能量。然而，人们认为这很令人担忧，并且如果在某些情况下不坚持，即使标准保护法不需要保护，也必须出错。在这里，我们重新访问了该实验，并表明尽管结果是正确的，但有一种方法可以规避它们并确保在这种情况下进行单个案例保护。该解决方案是非常不寻常的，挑战了量子力学的基本假设之一，即可以准备任何量子状态，并且涉及时期的，双重的非保守效应。我们的结果阐明了粒子初始状态的制备阶段的作用以及保护定律和参考框架的相互作用。我们还推测，当对任何保护实验进行这样的完整分析时，在每种情况下都会遵守保护。
Golay 码和量子语境
1949 年，戈莱（Golay）[1-4]发现了两种重要的纠错码。一种是二进制码，现用符号 1[24,12,8] 表示，由 2 12 = 4096 个 24 个字符（每个字符为 0 或 1）的码字组成，码字之间的最小距离为 2/8；另一种是三元码，用符号 [12,6,6] 表示，由 3 6 = 729 个 12 个字符（每个字符为 0、1 或 2）的码字组成，码字之间的最小距离为 6。3 在被发现后的几十年里，这些代码推动了编码理论和数学的重大进步。在编码理论中，戈莱码是唯一在有限域上可以纠正码字中多个错误的完美代码。 4 在数学中，二进制 Golay 码导致了 24 维 Leech 格子的发现 [5]，这种格子提供了该维度上最密集的全同球体堆积 [6]（已知的其他此类堆积的唯一维度是 8）。此外，在群论中，正如 Preskill [4] 所说，Golay 码启动了一系列事件，这些事件导致了上个世纪后期对有限群（特别是“零散”群）的完整分类。量子计算的出现以及由此产生的对量子纠错的兴趣，重新引起了人们对古典密码学的兴趣，因为人们意识到后者的许多结果可以改编并用于
（2+ ...）剪切粘度的经典和量子计算
表示在jmax=12处截断。我们还发现谱函数与频率的比值ρxyðωÞω在频率较小时呈现峰结构。在更大格子上超过jmax=12后，精确对角化方法和简单矩阵乘积态经典模拟方法都需要指数增长的资源。因此，我们开发了一种量子计算方法来计算延迟格林函数，并分析了计算的各种系统性，包括jmax截断和有限尺寸效应、Trotter误差和热态制备效率。我们的热态制备方法仍然需要随着格子尺寸呈指数增长的资源，但在高温下具有非常小的前因子。我们在Quantinuum模拟器和IBM模拟器上对小格子进行了测试，得到了与经典计算结果一致的结果。
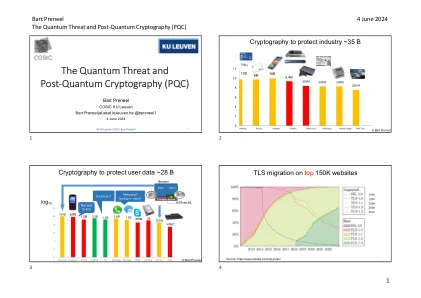
量子威胁和量词后加密（PQC）
•IAD将在不太遥远的未来开始过渡到抗量子抗算法的过渡•[…]•对于尚未过渡到Suite B椭圆曲线算法的那些合作伙伴和供应商，我们建议不要为此做出重大的支出，而是为了为即将到来的量子抗性量