XiaoMi-AI文件搜索系统
World File Search System在年轻人和老年人的主要抑郁症中基于坐标的网络映射:系统评价和荟萃分析
重大抑郁症(MDD)是全球残疾的主要原因之一(1),仅在美国,每年的生态负担总计估计超过2000亿美元(2)。MDD与慢性身体症状有关(3),自杀风险增加(4)和痴呆症(5)。虽然许多成人对MDD的研究通常集中于年轻和中年的成年人,但这种疾病会影响整个生命的人(6)。后期抑郁症(LLD)定义为55岁以上的个体中MDD的存在,与脑血管疾病(7)和Alz-Heimer病有关(8)。但是,LLD可以指55岁以上的人,患有抑郁症的史(早期发病),而55岁以上的人则是第一次出现抑郁症的人(晚期发作)。有些人认为LLD发病是一种“不同的”疾病,应该研究
引用的2坐标量造血调节途径,以维持稳态造血和移植中的HSC池
Hannah Lawson,Louie van de Lagemaat,Melania Barile,Andrea Tavosanis,Jozef Durko等。引用的2坐在稳态造血和移植中保持关键造血调节途径,以维持HSC池。干细胞报告,2021,16(11),pp.2784-2797。10.1016/j.stemcr.2021.10.001。hal-04140537
NAVSTAR,全球定位系统:其示例...
nAVStAr 1 全球定位系统 (GpS) 是第一个卫星导航系统,它使用户能够在十亿分之一秒内精确确定三维位置和时间,从概念发展为全面运作的系统仅用了二十多年时间。但这并不意味着推销这个想法很容易。早在 1969-1970 年,航空航天公司总裁兼 GpS 先驱伊万·盖廷就曾向理查德·尼克松总统的科学顾问李·杜布里奇建议成立一个总统委员会来审查卫星导航应如何进行,因为有太多的潜在用户。经过数周的思考,杜布里奇得出结论,执行盖廷的提议太难了。他告诉盖廷,“涉及的人太多,官僚机构太多,政治太多,机构太多。为什么不像我们以前那样让空军开发它呢?” 2
无本地效应在结构中取代
Zine Abdallah土木工程机构医生:Relizane University of University地址:Algeria resizane电子邮件:Abdellah.zine@uni-relizane.dz Berrabah Hamza Hamza Madjid土木工程机构医生hamzamadjid.berrabah@univ-relizane.dz Bouderba Bachir土木工程机构医生:Djillali University of Djillali Libes Sidi Bel Abbes地址:Algeria tissemsilt,Algeria电子邮件:bouderbabachir38@yahoo.fr摘要对非网站的影响,该研究对非网站的影响进行了临实,该研究均研究了非网站的影响。圆柱体,假设材料特性随厚度坐标的功率函数而变化。 位移表达式来自求解的微分方程,特别注意固定模式对位移的影响。 这些发现强调了非本地因素在确定结构行为和强调计算集成常数时考虑固定模式的必要性的重要性。 非局部效应表示相互作用和影响,这些影响超出了特定系统内观察到的条件或变化。 检查夹紧夹具的圆柱体,该研究深入到极性坐标的位移变化,同时考虑非本地效应的影响,假设材料特性会根据厚度坐标的功率函数而变化。 从解决的微分方程中衍生位移表达式形成了关键方面,其特定重点是固定模式如何影响位移。Zine Abdallah土木工程机构医生:Relizane University of University地址:Algeria resizane电子邮件:Abdellah.zine@uni-relizane.dz Berrabah Hamza Hamza Madjid土木工程机构医生hamzamadjid.berrabah@univ-relizane.dz Bouderba Bachir土木工程机构医生:Djillali University of Djillali Libes Sidi Bel Abbes地址:Algeria tissemsilt,Algeria电子邮件:bouderbabachir38@yahoo.fr摘要对非网站的影响,该研究对非网站的影响进行了临实,该研究均研究了非网站的影响。圆柱体,假设材料特性随厚度坐标的功率函数而变化。位移表达式来自求解的微分方程,特别注意固定模式对位移的影响。这些发现强调了非本地因素在确定结构行为和强调计算集成常数时考虑固定模式的必要性的重要性。非局部效应表示相互作用和影响,这些影响超出了特定系统内观察到的条件或变化。检查夹紧夹具的圆柱体,该研究深入到极性坐标的位移变化,同时考虑非本地效应的影响,假设材料特性会根据厚度坐标的功率函数而变化。从解决的微分方程中衍生位移表达式形成了关键方面,其特定重点是固定模式如何影响位移。该研究的结果突出了非本地因素在塑造结构行为中的关键作用,并强调计算整合常数时考虑固定模式的必要性。专注于夹紧的圆柱体,本研究探讨了在非本地效应的影响下极性坐标的位移变化,假定材料特性遵循
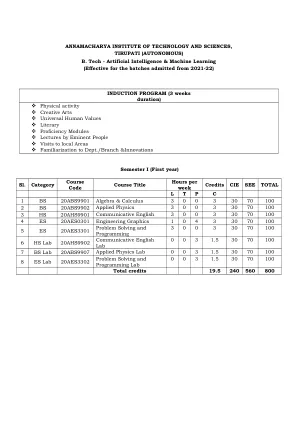
Annamacharya技术与科学学院
(自治)人工智能(AI)年:I学期:I研究分支:AIML课程代码年度和SEM代数和计算L T P C 20ABS9901 I-I 3 0 0 3课程成果:在学习课程后,学生将能够Co1。将矩阵代数技术应用于求解各种线性方程。二氧化碳。分析二次形式和平均值定理的线性变换。二氧化碳。将部分导数的基本概念应用于多变量函数。CO4。 评估笛卡尔,极性,圆柱和球形坐标的多个积分CO4。评估笛卡尔,极性,圆柱和球形坐标的多个积分
计算 Franck-Condon 因子
坐标 𝑖 是链接的。得到的 3N 对特征值和特征向量可以分为对应于平移运动的(其中三对)、对应于分子旋转运动的(除只有两对的线性分子外,其余均为三对)以及对应于振动自由度的。正是这 3N-6 个特征值和特征向量(对于线性分子为 3N-5 个)分别决定了分子的振动频率和简正模式。所有简正频率都不同,因此简正模式(指定三维空间中每个原子振动幅度的 3N 维向量)是线性无关的,并构成分子内部坐标的基础。如果我们只考虑分子内部坐标的 3N-6 空间,可以通过坐标变换进一步简化公式 (4)。将 𝑹 坐标系转换为“简正