XiaoMi-AI文件搜索系统
World File Search System跨学科、多部门合作......
*EASE:老年人生活活动空间项目 + INFINITY-ICOPE - 优化老年人功能独立性内在能力并阻止虚弱:新加坡 WHO-ICOPE 的健康老龄化适应性
理解和计划可持续性:旨在解决卫生社会决定因素的多部门社区伙伴关系指南
Mathematica创建了本可持续性规划指南,以支持多部门社区联盟和伙伴关系,以解决健康公平的社会决定因素,以提高健康公平并预防慢性病,这是改善健康社会决定因素(SDOH)的一部分 - 进一步获得更快的计划。该倡议是疾病控制与预防中心(CDC),全国县和城市卫生官员协会(NACCHO)与国家和地区卫生官员协会(ASTHO)之间的合作伙伴关系。为了促进合作和分享学习,NACCHO和ASTHO制作了本指南,并提供了可填补的计划模板,可供任何社区联盟或伙伴关系使用SDOH的伙伴关系。尽管本指南中的示例反映了由资助的联盟和合作伙伴关系解决的SDOH领域 - 建筑环境,粮食安全,社区临床联系,社会联系和免费政策 - 方法和策略适用于其他SDOH地区。NACCHO,ASTHO和CDC的反馈已通知并改进了本指南和模板。 我们还感谢您访问史塔克县的健康,社区联系,作为医学合作的食物,Live Allegheny Reach,马里兰州生活井卓越中心,Proviso Health的伙伴和西路易斯维尔户外娱乐倡议,以贡献他们的见解,以支持发展。 本指南可以独自使用,也可以与希望实现其政策目标的SDOH团队的政策计划指南一起使用。 我们希望它将帮助您发展一种支持您的SDOH目标并提高健康公平的学习文化。NACCHO,ASTHO和CDC的反馈已通知并改进了本指南和模板。我们还感谢您访问史塔克县的健康,社区联系,作为医学合作的食物,Live Allegheny Reach,马里兰州生活井卓越中心,Proviso Health的伙伴和西路易斯维尔户外娱乐倡议,以贡献他们的见解,以支持发展。本指南可以独自使用,也可以与希望实现其政策目标的SDOH团队的政策计划指南一起使用。我们希望它将帮助您发展一种支持您的SDOH目标并提高健康公平的学习文化。
建立多部门合作伙伴关系,以促进心血管疾病预防工作中的健康公平努力RFA信息网络研讨会2022年11月10日
支持地方卫生部门,以加强社区领导层的合作,以通过解决健康和改善健康的社会决定因素来加强心血管疾病的预防工作。
多部分量子态最优局部鉴别的界限
量子非局域性是多体量子系统的一个典型现象,它没有任何经典对应物。纠缠是最具代表性的非局域量子关联之一,它不能仅通过局域操作和经典通信(LOCC)来实现 1、2。众所周知,量子纠缠的非局域性质可用作许多量子信息处理任务的资源 3。量子非局域现象也可以出现在多体量子态鉴别中,这是量子通信中有效信息传输的重要过程。一般来说,正交量子态可以肯定地加以区分,而非正交量子态则无法做到这种区分。沿着这个思路,需要状态鉴别策略来至少以某个非零概率 4 – 7 鉴别非正交量子态。然而,当可用的测量仅限于 LOCC 测量 8 时,多体量子系统的某些正交态无法肯定地加以区分。由于在没有可能的测量限制时正交态总是能够被确定地区分,LOCC 测量的这种有限的鉴别能力揭示了量子态鉴别中固有的非局部现象。量子态鉴别的非局部现象也可能出现在鉴别多体量子系统的非正交态时;众所周知,某些非正交态不能仅使用 LOCC 9 – 11 进行最佳鉴别。因此,多体量子态 12 – 19 的最佳局部鉴别受到了广泛关注。然而,实现最佳局部鉴别仍然是一项具有挑战性的任务,因为很难对 LOCC 进行很好的数学表征。克服这一困难的一个有效方法是研究最佳局部鉴别的最大成功概率的可能上限。为了更好地理解最佳局部鉴别,建立实现这种上限的良好条件也很重要。最近,在二体量子态的局部最小误差鉴别中建立了最大成功概率的上限。此外,还给出了该上界饱和的必要充分条件20。在这里,我们考虑任意维数的多部分量子态之间的无歧义鉴别(UD)21 – 24,并为最佳局部鉴别的最大成功概率提供上限。此外,我们提供了实现该上界的必要充分条件。我们还建立了该上界饱和的必要充分条件。最后,我们使用多维多部分量子系统中的示例来说明我们的结果。本文组织如下。在“结果”部分,我们首先回顾多体量子系统中可分离算子和可分离测量的定义和一些性质。我们进一步回顾了UD的定义并提供了一些最优UD的有用性质(命题1)。作为本文的主要结果,我们给出了利用一类作用于多体希尔伯特空间的Hermitian算子实现最优局部鉴别的最大成功概率的上界(定理1)。此外,我们给出了Hermitian算子实现该上界的必要充分条件(定理2和推论1)。我们还建立了该上界饱和的必要充分条件(推论2)。我们通过多维多体量子系统中的例子说明了我们的结果(例子1和2)。在“方法”部分,我们提供了定理1的详细证明。在“讨论”部分,我们总结了我们的结果并讨论了与我们的成果相关的可能的未来工作。
通过单农杆菌系统简化植物基因沉默和基因组编辑物流,同时递送多部分病毒载体
图 1 JoinTRV 的设计,这是一种基于具有兼容来源的微型 T-DNA 载体的 TRV 表达系统。(A) 烟草脆裂病毒 (TRV) 的基因组组织。(B) TRV RNA2 工程用于序列克隆和表达。pLX-TRV2 的克隆盒图与 Bsa I 识别位点和 Bsa I 产生的突出端一起显示(底部)。LacZ 报告基因允许可视化选择重组载体;插入物的植物表达由豌豆早褐病毒 (PEBV) 外壳蛋白 (CP) 启动子驱动。(C) VIGS (pTRV2) 和 VIGE (pRNA2.PEBV) 中描述的 pLX-TRV2 和 TRV RNA2 载体的尺寸比较。(D) JoinTRV 系统图。两个 T-DNA 载体被多路复用到单个农杆菌细胞中,以同时递送 TRV 基因组成分。 pLX-TRV2 是 pLX-B2 衍生物,具有 pBBR1 来源和卡那霉素抗性基因 (npt I),pLX-TRV1 是 pLX-Z4 衍生物,具有 RK2 来源和庆大霉素抗性基因 (aac C1);由于这两个 T-DNA 载体具有兼容的来源和独立的抗生素选择机制,因此可以同时寄宿在同一细菌细胞中
用基于分叉的量子退火在自旋-1颗粒之间产生多部分纠缠
量子退火是解决组合优化问题的一种方法,其中量子闪烁是由横向场诱导的。最近,将基于分叉的量子退火与自旋-1颗粒一起退火为实施量子退火的另一种机制。在基于分叉的量子退火中,每种自旋均以| 0⟩,让这个状态以绝热的方式与时间有关的哈密顿量演变,我们发现了|在进化结束时±1⟩。在这里,我们提出了一种通过基于分叉的量子退火来在自旋-1颗粒之间生成多部分纠缠的方案,即GHz状态。,我们逐渐减少自旋1颗粒的失沟,同时绝热地改变外部驾驶场的幅度。由于自旋-1颗粒之间的偶极 - 偶极相互作用,我们可以在执行此协议后准备GHz状态。我们通过使用钻石中的氮空位中心讨论我们计划的可能实现。
是否应使用基因编辑来开发用于连续覆盖农业的作物?使用合作治理的多部门利益相关者评估
连续生物覆盖 (CLC) 农业整合多种作物,以创建多样化的农业生态系统,其中土壤在时间和空间上连续被活植物覆盖。CLC 农业可以大大提高农业生态系统的许多不同生态系统服务的产量,包括气候适应和缓解。要实现规模化,CLC 农业需要的作物不仅要提供连续的生物覆盖,而且要具有经济和社会可行性。目前,缺乏这种可行的作物严重限制了 CLC 农业的规模化。基因编辑 (GE) 可能为开发扩大 CLC 农业规模所需的作物提供强大的工具。为了评估这种可能性,一个广泛的多部门审议小组考虑了 GE 相对于替代植物育种方法的优点,作为改良 CLC 农业作物的手段。该小组包括许多需要其支持以扩大农业创新的部门,包括参与市场、金融、政策和研发的参与者。在本文中,我们报告了访谈和研讨研讨会的结果。相对于其他植物育种方案,小组中的许多人对利用 GE 开发 CLC 农业作物的前景充满热情。然而,小组指出了许多问题、风险和意外情况,所有这些都可能需要响应和适应性管理。相反,如果无法管理这些问题、风险和意外情况,则不太可能为此类应用维持强大的多部门支持基础,从而限制其扩展。新兴的负责任创新和扩展方法有可能管理这些问题、风险和意外情况;我们认为,如果使用这些新兴方法来管理此类项目,GE 作物用于 CLC 农业的结果可能会大大改善。然而,CLC 作物的 GE 和负责任的创新和扩展都是不完善的创新。因此,我们建议探索 CLC 作物 GE 的最佳途径是有意将这两种创新的实施和改进结合起来。更广泛地说,我们认为这种试点
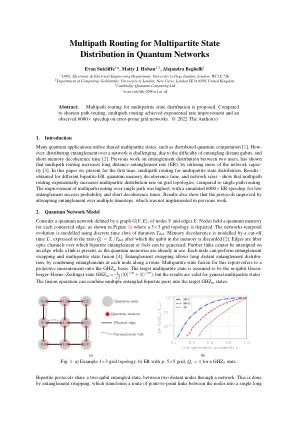
量子网络中多部分状态分布的多径路由
许多量子应用都利用共享的多部分状态,例如分布式量子计算[1]。,由于难以纠缠遥远的Qubits和短暂的记忆分解时间,因此在网络上分发纠缠是具有挑战性的[2]。以前关于两个用户之间纠缠分布的工作表明,多路由路由通过利用更多网络能力来提高长距离纠缠率(ER)[3]。在本文中,我们首次提出了多部分状态分布的多路径路由。结果 - 与单个路径路由相比,针对不同的双分部分,量子存储器分解时间和网络尺寸获得的网络大小 - 表明多径路由指数增加了网格拓扑上的多部分分布率。单个路径上的多径路由的改进最高,模拟的6000×ER加速度为低纠缠的成功概率和短的分解时间。结果还表明,通过尝试在多个时间步中尝试纠缠而改进的协议,这在先前的工作中未实现。
失神性癫痫遗传大鼠模型中的癫痫发作预测:通过多部位皮质-丘脑记录结合机器学习提高性能
癫痫发作预测是癫痫学的一大挑战。然而,人们致力于预测局灶性癫痫发作,而将全身性癫痫发作视为随机事件。在失神性癫痫大鼠的皮质丘脑系统八个位置采集包含数百个全身尖峰和波放电 (SWD) 的长持续时间局部场电位 (LFP) 记录,通过基于小波的算法在所有可能的两个或三个记录位置组合中进行迭代分析,计算小波能量信号同步性增加的乘积。比较了各种组合之间的预测灵敏度和误报率,并将真阳性和假阳性预测的小波谱输入随机森林机器学习算法以进一步区分它们。对皮层内和皮层丘脑 LFP 轨迹进行小波分析表明,与丘脑内组合相比,其误报数量明显较少,而基于体感皮层 IV、V 和 VI 层记录的预测在预测灵敏度方面明显超过所有其他组合。在对九只来自斯特拉斯堡的遗传性失神癫痫大鼠 (GAERS) 的 24 小时样本外记录中,包含 SWD 发生率的昼夜波动,通过训练后的随机森林对真阳性和假阳性进行分类,进一步将误报率降低了 71%,尽管在误报和预测灵敏度之间有所权衡,这反映在相对较低的 F1 分数值上。结果支持失神癫痫的皮层焦点理论,并得出 SWD 在一定程度上是可预测的结论。后者为闭环 SWD 预测预防系统的开发铺平了道路。概述了可能转化为人类数据的建议。