XiaoMi-AI文件搜索系统
World File Search System与老虎机问题相关的策略驱动极限定理
受对老虎机问题渐近行为研究的启发,我们得到了几个策略驱动的极限定理,包括大数定律、大偏差原理和中心极限定理。与经典极限定理不同,我们开发了抽样策略驱动的极限定理,这些定理可以产生最大或最小平均回报。大数定律确定了各种策略下可以实现的所有可能极限。大偏差原理提供了偏离极限域的最大衰减概率。为了描述围绕平均值的波动,我们得到了最优策略下的策略驱动的中心极限定理。这些定理中的极限是明确确定的,并且在很大程度上取决于事件的结构或积分函数和策略。这展示了学习结构的关键特征。我们的结果可用于估计最大(最小)回报,并确定避免双臂老虎机问题中帕隆多悖论的条件。它也为通过统计推断确定提供更高平均奖励的臂奠定了理论基础。
欧盟创新政策 - IEP@BU
成员国提出的最低标准(约九成)是辅助性原则的支持者。我们在此只需指出,有充分的理由说明为什么辅助性原则不适用于我们的背景。将部分资金转移到欧盟层面可能会带来许多好处。它将扩大可供选择的项目库,以及可以对这些项目提供明智意见的独立专家库。它会增加首席研究人员和审稿人之间的(物理、文化、社会)距离,使审查过程更加公正。最后,具体到颠覆性创新的情况,雄心勃勃的研发注定会以不可忽略的概率失败,这意味着如果很少有项目成功,就很难进行高级研究而不冒着引起媒体强烈反对的风险。欧盟层面的大数定律使这种情况发生的可能性降低。
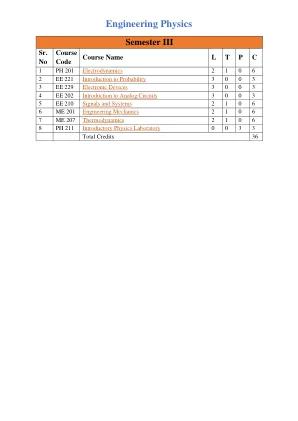
工程物理学
简介:学习本课程的动机、必修基础数学复习、实线子集上概率与长度的关系、概率形式定义、事件与$\sigma$代数、事件独立性与条件概率、事件序列与Borel-Cantell引理。随机变量:随机变量的定义、随机变量的类型、CDF、PDF及其性质、随机向量与独立性、随机变量变换简介、高斯随机向量简介。数学期望:通过例子了解平均值的重要性、期望的定义、矩与条件期望、MGF、PGF与特征函数的使用、方差与k阶矩、MMSE估计。不等式与收敛概念:马尔可夫、切比雪夫、切尔诺夫与Mcdiarmid不等式、概率收敛、均值与几乎必然、大数定律与中心极限定理。随机过程的简要介绍:示例和正式定义、平稳性、自相关和互相关函数、遍历性的定义。
平面随机增长模型中的波动下限
即使经过多年对随机增长模型(如首次和最后一次渗透和定向聚合物)的研究,许多问题在技术上仍然是神秘的或遥不可及的。例如,除了保证通过时间/自由能的线性增长率的基本形状定理之外,还存在亚线性波动,其渐近性尚未建立。即使在平面设置中,对于该设置,推测图景很清晰,但一般工具远不能使其严格。这与可积模型形成鲜明对比,可积模型的波动指数只是已证明的一小部分。在本文中,我们考虑了三个广泛研究的随机增长模型:首次渗透(FPP)、最后一次渗透(LPP)和随机环境中的定向聚合物。虽然这些模型在衡量增长的方式上有所不同,但它们都拥有一个大数定律,即增长率是渐近线性的。然而,更神秘的是亚线性波动。在二维版本中,这些模型被认为属于 Kardar–Parisi–Zhang 普适性类 [30],尤其是增长涨落的阶数为 n 1 / 3。除了 LPP 和定向聚合物具有精确可溶性的特殊情况外,严格的结果与这一目标相去甚远,在某些情况下甚至不存在。本文的目标有两个。首先,我们描述一种通用策略,用于证明随机变量序列(在定义 2.1 中明确定义)涨落阶的下界。该方法改编自第二作者最近在 [23] 中开发的技术。它很通用,因为它可以用于由独立同分布随机变量组成的各种问题,其中不对这些变量的共同分布做出任何假设。其次,我们应用该方法研究平面 FPP、LPP 和定向聚合物的生长涨落。在这三种情况下,我们都能证明 √ log n 阶波动的下限。此外,对于 FPP,我们扩展了形状
强劲的社会市场经济
稳健的社会市场经济——关于新冠疫情的一些思考 当前这场始于中国武汉的疫情给全世界带来了沉重打击,而全世界对这场危机都毫无准备。金融市场的工作是预测未来发展并根据预期调整价格,但这次疫情却出乎意料。道琼斯指数暴跌超过 20%,经历了历史上损失百分比最大的一周。全球个体经营者和中小企业担心破产。各国政府和央行正试图通过前所未有的支出和信贷来提振经济,这些措施远远超过了十年前的水平,从而冒着通货膨胀、货币危机或另一场债务危机的风险。当这场危机结束时,人们会问:我们怎么会愚蠢到让这种情况发生?我们为什么要开放边境?为什么我们在为时已晚的时候关闭边境?我们为什么(再次)让意大利失望?为什么他们告诉我们口罩毫无用处,尽管它们的用处显而易见?为什么他们告诉我们关闭学校没有意义,却在一周后关闭学校?这些都是很好的问题,也许一些政客必须为他们的疏忽付出代价。然而,问问自己总是好的:如果我是一名政客,我将如何应对病毒爆发的可能性?我会做好准备吗?既然不可能为所有事情做好准备,我们可能会问,我们能为我们的市场和社会做些什么,以帮助他们度过未来的风暴。在二十一世纪,世界第二次受到“小事件”的重创。2008 年,金融市场一直在猜测信贷风险,忽略了许多小额信贷借款人同时破产的可能性;交易员相信大数定律,该定律适用于许多小的、独立的、统计上相同的情况,但不适用于许多小事件可能通过某些共同因素高度相关的情况。监管不当引发的猜测越来越多,游戏一直进行到不可思议的事情发生,如今著名的“黑天鹅”登场。这些天,世界又被另一件小事件震惊了,那就是由病毒引起的全球大流行。当然,这种大流行的可能性是众所周知的。事实上,德国政府肯定早就意识到了这种可能性,因为它在 2012 年要求罗伯特·科赫研究所对新冠病毒大流行的潜在后果进行研究。当你阅读这项研究时,你不禁会问:为什么当局没有对这项研究作出反应?没有反应的原因可以称为“忽视小事件”或“奈特不确定性”。芝加哥经济学家弗兰克·奈特是第一位强调小事件重要性的社会科学家,我们不知道这些事件发生的概率,也无法合理地估计它们对现代经济的影响。在金融危机期间,市场忽视了大量信贷事件同时发生的可能性,监管机构甚至允许他们忽略这种不确定性。现在,政客、市场和卫生当局显然已经确信没有必要为病毒大流行做准备,他们可能认为这种准备的成本太高了。