XiaoMi-AI文件搜索系统
World File Search System电信及电子设备帐篷及仓库安装服务
我保证。 “ (k) 承诺书中关于“排除黑社会团体的事项”的内容有虚假记载或发生违反承诺书的情况时。 (k) 投标人提交未经政府批准的同等产品时。 (4) 合同的准备 中标人被选定为中标人后,应立即准备合同。 (5)特别条款 本协议受“服务合同条款”、“关于撞船等违法行为的特别条款”、“关于排除有组织犯罪集团的特别条款”的约束。 (6)中标人确定方式:投标总额在竞买队确定的估价限额内的投标人即为中标人。如果有两名或两名以上最低出价者有资格中标,则将通过抽签方式确定中标者。 在确定中标人时,中标价格为投标文件所载金额加上该金额的10%(如果该金额有不足1日元的小数部分,则小数部分四舍五入)。因此,无论投标人是消费税的应税商业实体还是免税商业实体,投标人都必须在其投标文件中载明相当于估算金额的110/100的金额。 (7)现场通报会地点和日期/时间:a)地点:日本陆上自卫队俱知安基地。b)日期和时间:2024 年 7 月 16 日星期二 08:30 至 16:30 至 2024 年 8 月 6 日星期二(周六、周日除外)。 如果需要进行现场检查,则必须在现场检查前一天根据(8)(K)规定安排日期和时间,并且必须在政府官员面前进行检查。此外,如果您在未勘察现场的情况下参与投标,则必须自行负责检查现场勘察期间给出的问题和答案后再参与。 (可选格式) 若有身份不明人士参与竞标,该人士必须同意在参与竞标前不就有关事宜作出任何投诉。 (8)其他 a.本合同自双方签字、盖章之日起成立。 (一)投标人参加投标时须提交资格审查结果通知书复印件。 如果您代表其他人竞标,则必须提交授权委托书。 E. 允许通过邮寄方式投标。在这种情况下,请在信封上清楚地写上“(投标主题)随附投标文件”,并附上资格审查结果通知的副本,并在2024年8月19日星期一下午5点之前通过挂号信(简单挂号信也可以)将其发送至俱知安驻地第325会计部队俱知安支队。此时请您致电负责人确认到达情况。 重新招标将在政府指定的时间进行。 本次招标将以邮寄方式进行。因此,如果您希望当天参加,请于 2024 年 8 月 19 日星期一下午 5:00 联系俱知安驻地第 325 会计部队俱知安支队。 投标相关咨询处:陆上自卫队俱知安驻地第 325 计画中队俱知安支队承包课(负责人:星野 / 石川)电话:0136-22-1195(内线 463)规格相关咨询处:陆上自卫队俱知安驻地北部机动监视部队(负责人:日置 / 中市)电话:0136-22-1195(内线 556) (8)公告发布地点及期限 A.公告发布地点:俱知安驻地 B.北部战区司令部网站:http://www.mod.go.jp/gsdf/nae/fin/index.html C.公告发布期限:2024 年 7 月 16 日(星期二)至 2024 年 8 月 20 日(星期二)
电子功能材料研究中心
●涵盖了多种用于光学应用的晶体:激光和非线性光学晶体,磁光晶体,闪烁体/剂量计晶体,宽带隙半导体,压电和铁电晶体等等等等。●我们当前的主要研究目标是:用于高亮度照明设备的单晶磷光器。用于激光机械的光学隔离器的法拉迪旋转器。用于高温使用的压电晶体,例如燃烧压力传感器。氧化包胶作为新型宽带隙半导体。用于IR光学应用的Chalcogenide●积极促进与大学,国立研究所和行业的合作,并积极追求国际合作,以促进新的观点和原始思想。
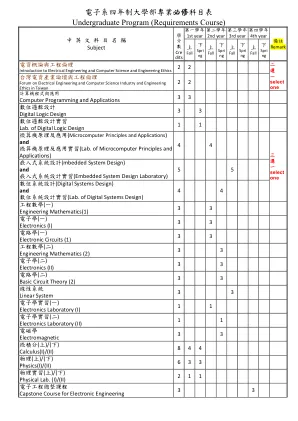
半导体工程学系固态电子组
【半导体工程学系的优势】【半导体工程学系的优势】,每学期定期举办全系导生活动,每学期定期举办全系导生活动,24 小时开放之教学实验室、学生读书室、学生图书室及研讨室。 小时开放之教学实验室、学生读书室、学生图书室及研讨室。※,(如台积电)暑期实习。(如台积电)3+2 uiuc电机所双联(uiuc电机所双联)(uiuc电机所双联)※※※※※※※※,补助出国奖学金至国外大学进行交换学生(一学期或一学年),补助出国奖学金至国外大学进行交换学生(一学期或一学年)欢迎与半导体工程学系联系(一学期或一学年)欢迎与半导体工程学系联系https://nano.nycu.edu.tw:(1)请务必于113/4/5(五)至113/5/5(2)至半导体工程学系官网填写出席调查回条。(2)5/17(2)5/17(2)5/17(五)
苏州贝克微电子股份有限公司BatelabCo.,Ltd.
要约价格预计将取决于唯一的整体协调员(本身和代表承销商)与公司确定日期之间的一致性,预计将在2023年12月22日星期五左右,但无论如何,无论如何,无论如何,在2023年12月22日(12月22日星期五)中下午12:00,不得晚于2023年12月22日星期五。要约价格预计不超过每股38.45港元的港元,而且预计不少于每股27.47港元,除非另有宣布。香港要约股的申请人必须按申请支付每股38.45港元的最高要约价格,同时经纪1.0%,AFRC交易税为0.00015%,SFC交易税,0.0027%的0.0027%和证券交易所交易交易税,如果股票为0.00565%,则比股票较少,如果股价为0.00565%,则比HK价格较低。如果出于任何原因,该公司与唯一的整体协调员(本身和代表承销商)在2023年12月22日(星期五)中午或之前在2023年12:00中午之前或之前均不同意要约价格,则全球募股(包括香港公共奉献)将不会进行和乐意。
拭子 无菌聚酯拭子 #STX764
TX705P STX705P TX720B STX763 STX764 头部材料 棉/100 ppi 聚氨酯泡沫 棉 棉 棉/100 ppi 聚氨酯泡沫 短纤维涤纶 短纤维涤纶 头部宽度 13.5 毫米 (0.531 英寸) 7.0 毫米 (0.276 英寸) 7.0 毫米 (0.276 英寸) 11.8 毫米 (0.465 英寸) 5.8 毫米 (0.228 英寸) 4.6 毫米 (0.181 英寸) 头部厚度 13.5 毫米 (0.531 英寸) 7.0 毫米 (0.276 英寸) 7.0 毫米 (0.276 英寸) 10.0 毫米 (0.394 英寸) 5.8 毫米 (0.228 英寸) 4.6 毫米 (0.181 英寸) 头部长度 28.0 毫米 (1.102 英寸) 17.0 毫米 (0.669 英寸) 17.0 毫米(0.669") 26.3 毫米 (1.035") 18.0 毫米 (0.709") 17.0 毫米 (0.669") 手柄材质 木材 木材 聚苯乙烯 木材 聚苯乙烯 聚苯乙烯 手柄宽度 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 手柄厚度 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 2.5 毫米 (0.098") 手柄长度 126.0 毫米 (4.961") 135.0 毫米 (5.315") 135.0 毫米(5.315") 127.0 mm (5.000") 134.0 mm (5.276") 134.0 mm (5.276") 拭子总长度 154.0 mm (6.063") 152.0 mm (5.984") 152.0 mm (5.984") 154.0 mm (6.063") 155.0 mm (6.102") 155.0 mm (6.102") 头部粘合 机械粘合剂 粘合剂 热/机械水基粘合剂 水基粘合剂 手柄颜色 棕色 棕色 白色 棕色 白色 白色 设计说明 泡沫头机械固定在棉签芯上;长木柄
引导服务线
DC Water 的无铅 DC 计划旨在实现一项雄心勃勃的目标,即到 2030 年公平地拆除所有铅服务线。自 2019 年以来,我们更多地了解了整个特区的铅服务线位置、如何高效地完成全区范围内的铅服务线拆除,以及与客户就更换计划进行沟通的有效方式。我们利用这些经验教训修订了 2021 年铅服务线更换计划,以确保我们在 2030 年前拆除和更换特区内的每一条铅服务线。在该计划中,我们描述了最近的现场调查和更换工作的结果如何促使我们重新评估原始服务线清单的准确性。我们仔细检查了用于制定初始清单的所有数据源,并将特区内的所有服务线分类为已验证的铅服务线、疑似铅服务线、无信息(没有管道材料记录的服务线)、疑似非铅服务线和已验证的非铅服务线。此更新的库存分类系统为 DC Water 在估计特区内剩余的铅服务线时提供了更高的置信度。为了最终确定可疑的服务线是铅还是非铅,我们正在调查和验证任何被归类为可疑铅、可疑非铅或没有信息的房屋的服务线材料。在我们将要调查的房屋中,我们估计其中大约有 42,000 所房屋需要更换。随着我们在现场了解更多信息,我们将更新清单并在 Lead Free DC 网站上实时与公众分享。