XiaoMi-AI文件搜索系统
World File Search System对角线
![arXiv:2111.01457v4 [cs.SD] 2022 年 10 月 31 日](/simg/c\cb1162b508e7d25d9394ae5d0bc21f4c32769d20.webp)
arXiv:2111.01457v4 [cs.SD] 2022 年 10 月 31 日
图 6 示例性注意力矩阵，可视化三位参与者在收敛时的注意力得分（来自随机选择的训练样本）（值越亮表示注意力得分越高）。解码器中的时间步长在 y 轴上表示，编码器的时间步长在 x 轴上表示。对角线结构表明注意力得分在时间域上是很好地对齐的，例如输出中的后续步骤关注输入中的后续步骤。该图还表明，填充输入 sEEG 序列（语音规划和理解）可能是不必要的，因为没有太多注意力放在第一个和最后一个输入步骤上。
使用编码器-解码器框架从颅内深度电极合成语音
图 6 示例性注意力矩阵，可视化三位参与者在收敛时的注意力得分（来自随机选择的训练样本）（值越亮表示注意力得分越高）。解码器中的时间步长在 y 轴上表示，编码器的时间步长在 x 轴上表示。对角线结构表明注意力得分在时间域上是很好地对齐的，例如输出中的后续步骤关注输入中的后续步骤。该图还表明，填充输入 sEEG 序列（语音规划和理解）可能是不必要的，因为没有太多注意力放在第一个和最后一个输入步骤上。
Promise-Bptime层次定理上的注释
层次结构定理是复杂性理论的基本结果。他们指出，随着计算资源的增加，人们可以严格解决更多问题。bptime的时间层次结构定理仍然是一个臭名昭著的难以捉摸的话题。迄今为止，只有在提供对数或恒定建议位时才知道，bptime的无条件层次结构定理[BAR02，FS04，GST11，FST11，FST11，FST05，PER05，VMP07]。此外，已知层次结构定理对BPP的完全问题[BAR02]持有条件。与确定性[HS65，HS66]或非确定性时间层次结构[COO72，SFM78，ˇ Z´AK83]，BPTIME的层次定理保持开放，因为在实用上，似乎有效地确定一个随机的Turning机器是无效的，是否可以有效地确定一个随机的机器被拒绝或不拒绝，或者拒绝了一个有界的错误或不符合界限。因此，标准对角线化在列举所有随机图灵机的步骤上失败，并具有有界的双面误差。实际上，确定每个输入的随机图灵机是否有界限。这种情况在其承诺版本中被认为不同。Pr -bptime的时间层次结构（承诺概率时间课）是一种民间传说的陈述，在谈话，课程和流行的教科书中出现了，例如[AB09]。我们观察到没有来源勾勒出其证明，并且可能假定其有效性是从直接对角线化的，或者遵循存在完全问题的Pr -bptime；参见例如[GAJ22]。在高水平上，对角度化的关键步骤涉及否定枚举的图灵机的输出。但是，我们观察到基于直接对角线的直接对角度或证据（例如，减少到Bptime完全问题[BAR02]）并不容易通过PR- BPTIME层次定理携带。通过否定输出，构造的语言
主校园停车地图06-2019.PUB
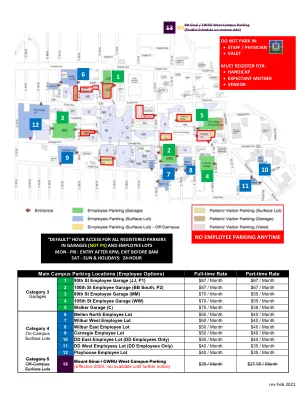
超大车辆信息超大车辆停车位于MM（89）4楼，WW（105）4楼和JJN（93）2楼，超大车辆区域由对角线条纹空间定义。超大空间旨在容纳通常超过标准空间边界的车辆。当开发区域已满时，超大车辆不在坡道上停车。车辆在指定的坡道空间内不完全构成驾驶员和看护人行走的障碍/危害，并受到执法的影响。注意不符合超大车辆的车辆包括•所有汽车和轿车•所有小型货车•所有紧凑型公用事业车辆•所有跨界车辆超大车辆都可能包括（但不限于）
使用土工格里德对混凝土的某些特性的影响
地理植物是由聚乙烯，聚酯和聚丙烯等聚合物制成的地质材料。它们通常在土木工程应用中使用，以提供土壤拉伸的加固。地理植物用于建造基础，挡土墙，路边和陡峭的斜坡。它们由柔性网稳定在固定壁后面的土壤以产生增强的相干质量。结构由两对肋骨组成，这些肋骨在两个不同的方向上交叉。一组肋骨平行于机器的方向，而第二组（称为跨机动方向）垂直于机器的方向。取决于纵向和对角线肋骨的排列方式，孔（肋骨之间的空间）的范围从150到250毫米。肋骨具有通常大于肋骨并通过粘结，交织或挤出连接的孔或孔（Yousif等，2021）。
DNA 6323 ADB110020 DTL870361
mis 报告是一份以人员为导向的国防部参与地下核武器试验的历史，包括 1969 年 9 月 12 日至 1972 年 5 月 2 日期间的“曼德尔”和“索环”行动、“分钟牛排”试验、“柴油列车”试验、“黛安娜雾”试验、“薄荷叶”试验、“哈德逊月亮”试验、“对角线”试验和“迷雾北”试验。该报告是一系列历史报告中的第四份，该系列报告将包括所有国防部地下核武器试验和所有能源部地下核武器试验，这些试验自 1962 年以来分布显著。除了这些历史卷之外，一个限制分发卷将确定所有国防部参与者（军方、民间和国防部承包商），并列出他们的辐射剂量数据。
学术手册B.Tech计划
模块1：矩阵和应用程序 - 矩阵：矩阵操作 - 附加，标量乘法，乘法，转置，伴随及其属性；线性方程和高斯消除，决定因素及其特性的系统；克莱默的统治；向量空间：子空间，线性依赖/独立性，基础，维度，r^n的标准基础，线性变换，线性变换的矩阵，基础和相似性的变化，rank-nullity定理；内部产物空间，革兰氏阴性过程和正统基础，特征值和特征向量，特征多项式，对角线化。模块2：单个变量的差分计算函数：函数和先验函数；限制，连续性和不同性；平均价值定理，泰勒和麦克拉林的定理；参数方程和极坐标。几个变量的函数：部分分化；总分，欧拉的定理和概括；
![arxiv：2404.15547V2 [cond-mat.str-el] 2024年8月26日](/simg/6\6461acb7396b7fc3bfabe3bc3d65aec07cc9a880.webp)
arxiv：2404.15547V2 [cond-mat.str-el] 2024年8月26日
我们考虑在填充因子8 /17处的分数量子霍尔效应（FQHE），其中在双层石墨烯的Zeroth Landau水平上观察到了不可压缩性的特征。我们提出了一个用“（8/3）21 3” Parton波函数描述的Abelian状态，其中Parton本身形成了FQHE状态。该状态在拓扑上与摩尔阅读状态的女儿状态的8/17 Levin-Halperin State不同。我们在双层石墨烯的Zeroth Landau水平的8/17处进行了库仑相互作用的广泛数值精确对角线化，但发现我们的结果无法最终确定基本基态的拓扑顺序。我们将（8 /3）21 3边缘的低能效率理论进行了预测，并对该状态的实验可测量特性进行了预测，该特性可以证明它除了8/17 levin-halperin状态。