XiaoMi-AI文件搜索系统
World File Search System希尔查科技有限公司
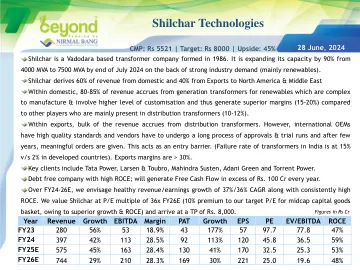
稳定 / 关怀 A2 附件 -1 中的设施详情 理由和关键评级驱动因素 Shilchar Technologies Limited (STL) 的银行设施评级修订考虑到其经营规模和盈利能力的显着改善,得益于 FY24(FY 指的是 4 月 1 日至 3 月 31 日期间)出口和国内销售额的增加,从而加强了债务覆盖率指标、增加了净值基础和充足的流动性。评级还考虑了其订单量显着增加。评级继续从发起人的丰富经验、其既定的经营记录以及信誉良好的客户群中获得优势。然而,由于其在竞争激烈的利基行业中的地位、声誉良好但中等集中的客户群以及其利润率易受原材料价格和外汇汇率波动的影响,评级继续受到限制。评级敏感性:可能导致评级行动的因素积极因素
伯克希尔股息策略
只要有吸引人的候选人,投资组合将试图在广泛的经济领域中广泛多样化。虽然投资组合将在很大程度上“自下而上”对宏观因素的某些考虑可能扮演较小的角色。在任何一个给定的时间,某些投资组合(总计)似乎比另一个投资组合更具吸引力(明智的或估值)。但是,通常不应该发生相对于基准的大型或极端部门的浓度。总共寻求最终的投资组合:降低系统风险,质量高于平均水平和降低的波动性。从现金流的角度来看,我们认为典型的伯克希尔持有量可以每年至少提供7.5%的现金流量增长,而且投资组合的收益率应超过标准普尔500指数。如果我们的公司可以提供收入和股息明智,那么有吸引力的赞赏应遵循,从而提供了强大的总回报特征。
穆罕默德·贾姆希尔
Jamsheer K. 博士于 2017 年获得新德里国家植物基因组研究所的博士学位,研究领域为植物细胞信号传导和发育。他曾在法国斯特拉斯堡植物分子生物学研究所担任 EMBO 短期研究员,并在新德里国家植物基因组研究所担任研究助理,接受博士后培训。他研究植物营养和压力感知机制以及信号通路。2018 年,Jamsheer 博士获得印度政府颁发的著名 DST- INSPIRE 教职奖学金,并加入北方邦阿米蒂大学。他曾获得多项重要的国家和国际奖项、奖学金和旅行补助金,如 2020 年 INSA 青年科学家奖章、EMBO 短期奖学金、EMBO 旅行补助金、NIPGR-最佳论文奖等。Jamsheer 博士的主要研究重点是了解真核生物营养和应激途径所涉及的基本细胞信号传导机制。这些信息将用于使用基因组编辑和传统基因工程工具对单细胞真核生物和高等植物进行工程改造,使其具有理想的性状。
海军作战基地希尔战区
场地描述:二战期间关岛海军基地关押的日本战俘使用 20 世纪 30 至 40 年代流行的砌筑技术建造了这座露天剧场。该设施因靠近海军作战基地 (NOB) 总部而得名,该总部位于海军陆战队大道对面,靠近今天的 CDR William C. McCool 学校。这座露天剧场占据了整个山坡,可容纳 5,000 多人坐在沙袋或木凳上。这座剧场在 20 世纪 50 年代末被充分利用,之后被废弃。直到 1993 年 11 月,美国海军工程营才通过清理杂草丛生的丛林,让这片土地重获生机,露出了至今仍存在的 NOB Hill 剧场。
人工智能研究所希尔日小册子
虽然研究人员长期以来一直在追求这一目标,但最近这两个领域的突飞猛进为重大发现带来了希望。过去十年,人工智能取得了显著进步,产生了具有令人印象深刻能力的解决方案。例如,当前的语言模型可以令人信服地模仿人类在基于文本的交互中的对话能力。然而,我们正面临“莫拉维克悖论”,即人工智能在挑战人类的任务中表现出色,但在人类认为毫不费力的任务中却失败了。例如,计算机在国际象棋方面的表现优于人类,但 3 岁的孩子可以比机器人更好地移动棋子。人工智能在所谓的高级领域(例如语言和围棋和国际象棋等困难游戏)中表现出色,而导航和跑步等较低级任务是人类明显胜过人工智能和机器人的领域。
伯克希尔经济战略 2025-2035
3. 初步研究:计划与伯克希尔全境和地方层面的主要利益相关者和合作伙伴进行磋商,介绍我们的主要发现,并就他们的优先事项和他们认为需要改变的地方征求他们的意见