XiaoMi-AI文件搜索系统
World File Search SystemSTAAR 标准快照 – 代数 I
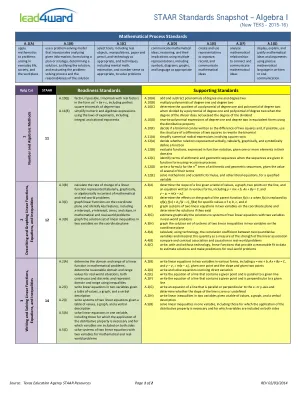
A.10(A) 对一次和二次多项式进行加减运算 A.10(B) 将一次和二次多项式相乘 A.10(C) 当除数的次数不超过被除数的次数时,确定一次多项式和二次多项式除以一次多项式和二次多项式后的商 A.10(D) 利用分配律将一次和二次多项式表达式重写为等价形式 A.10(F) 判断二项式是否可以写成两个平方差,如果可能,使用两个平方差的结构重写二项式 A.11(A) 简化涉及平方根的数值根式表达式 A.12(A) 判断以口头、表格、图形和符号表示的关系是否定义函数 A.12(B) 给定函数定义域中的一个或多个元素,计算以函数符号表示的函数A.12(C) 当算术和几何序列以函数形式给出时,使用递归过程识别序列的项 A.12(D) 写出第 n 个公式
9 认识特殊二项式策略
中级代数技能培养 # PF – 9 识别特殊二项式策略:确定两个项是完全平方数还是完全立方数。然后检查形式是否为以下之一:平方和平方差立方和立方差示例 1. 3 8 x − = 2. 4 25 y − = 3. 4 8 16 ab − =
互补性确定SARS-COV-2混合免疫中的区域
疫苗接种前SARS-COV-2感染可以促进COVID-19疫苗接种和vaccination后突破性SARS-COV-2感染引起的保护,可以促进COVID-19疫苗接种的现有免疫力。这种“混合免疫”对SARS-COV-2变体有效。为了理解分子水平的“杂交免疫”,我们研究了抗RBD(受体结合结构域)抗体的互补性确定区域(CDR)(CDR),这些抗体从具有“杂种免疫”的个体中分离出来,以及从“幼稚”(不是SARS-COV-2感染)疫苗的个体中分离出来的。CDR分析是通过液相色谱/质谱 - 质谱法进行的。 主要成分分析和部分最小平方差分分析表明,CoVID-19接种疫苗的人共享CDR Pro填充物,并且预疫苗发生的SARS-COV-2感染或突破性感染进一步塑造了CDR ProFile,并在杂种中具有CDR PREFLE,而无需接种CDR疫苗,而无需感染CDR疫苗。 因此,我们的结果表明,杂交免疫的CDR率与疫苗接种引起的CDR ProFE不同。CDR分析是通过液相色谱/质谱 - 质谱法进行的。主要成分分析和部分最小平方差分分析表明,CoVID-19接种疫苗的人共享CDR Pro填充物,并且预疫苗发生的SARS-COV-2感染或突破性感染进一步塑造了CDR ProFile,并在杂种中具有CDR PREFLE,而无需接种CDR疫苗,而无需感染CDR疫苗。因此,我们的结果表明,杂交免疫的CDR率与疫苗接种引起的CDR ProFE不同。
人力资本如何影响印度的经济增长......
表 1:描述统计变量 LnGDP LnPC LnHC LnTO LnINF 平均值 15.227 13.818 1.702 29.329 59.423 中位数 15.200 13.736 1.734 24.258 51.078 最大值 16.394 15.235 2.124 55.794 159.830 最小值 14.197 12.597 1.285 12.219 9.737 标准差0.658 0.852 0.261 14.779 44.823 偏度 0.141 0.176 -0.048 0.468 0.885 峰度 1.811 1.670 1.687 1.730 2.683 Jarque-Bera 2.364 2.996 2.744 3.937 5.124 概率 0.307 0.224 0.254 0.140 0.077 总计 578.622 525.067 64.673 1114.509 2258.062 总计平方差16.029 26.876 2.515 8081.719 74335.350 观测值 38 38 38 38 38 来源:作者估计
基础心率和短暂的日期可靠性
摘要简介本研究确定了(1)日至日的可靠性(HR)和HR可变性(HRV)通过Equivital EQ02+ LifeAnitor测得的(HRV),以及(2)与短期HRV相比,超短期HRV的一致性。方法二十三名现役的美军士兵(5名女性,18名男性)完成了两次实验访问,距离> 48小时,限制与基础监测(例如,运动,饮食)一致,在俯卧撑休息后,在20-21分钟(超短期)(超短期)和20-25分钟(短期)(短期)(短期)(短期)(短期)(短期)(短期)。HRV作为R – R间隔(SDNN)的SD和连续R – R间隔(RMSSD)之间平方平方差的平方差的平方根。结果使用线性混合模型方法的日常可靠性(INSERS INTACERISS相关系数(ICC))适用于HR(0.849,95%CI:0.689至0.933)和RMSSD(ICC:0.823,95%CI:0.623至0.920)。SDNN具有适度的日常可靠性,随着更大的变化(ICC:0.689,95%CI:0.428至0.858)。考虑呼吸作用时,RMSSD的可靠性略有提高(ICC:0.821,95%CI:0.672至0.944)。没有测量1分钟的人力资源偏差与5分钟(p = 0.511)。在1分钟的测量值与5分钟的测量值中,SDNN的平均偏置为-4 ms,RMSSD的平均偏置为-4 ms(p≤0.023)。结论是在使用基础主导和测量呼吸一致的限制之前进行20分钟稳定周期之前的结论时,军事人员可以依靠EQ02+进行基础HR和RMSSD监测,但使用SDNN应该更加谨慎。这些数据在遵循这些过程时还使用超短期测量值支持。
JHEP06(2022)062
中微子振荡最早由 Bruno Pontecovero 于 1957 年 [1] 提出,并被用于解决大气中微子异常和太阳中微子之谜。1998 年的超级神冈中微子探测实验 (Super-K, SK) [2] 和 2002 年的萨德伯里中微子天文台 (SNO) [3] 通过实验证实了这一点;更多详细信息请参阅参考文献 [4]。大多数中微子振荡实验都可以在具有三个大质量中微子的标准模型 (SM) 中得到很好的解释。在标准的三味中微子振荡框架中,三种已知的中微子味本征态(νe、νµ和ντ)可以写成三个质量本征态(ν1、ν2和ν3)的量子叠加,中微子振荡概率用六个振荡参数表示:三个混合角(θ12、θ13和θ23)、两个质量平方差(∆m221和∆m231)和一个狄拉克CP相(δCP)。如果中微子是马约拉纳粒子,则马约拉纳CP相对中微子振荡不起作用。在这六个可观测量的振荡参数中,∆m221、| ∆ m 2 31 |、θ 12 和 θ 13 已精确测定到百分之几的水平。但中微子质量排序(∆ m 2 31 是正还是负)、θ 23 的八分之一(θ 23 大于还是小于 45 ◦)和狄拉克 CP 相仍是悬而未决的问题。目前,正常质量排序 (NMO) 和 θ 23 的第二八分之一均低于 3 σ 置信水平 (CL) [ 4 – 6 ],在 3 σ CL 下,NMO 的 δ CP 范围为 [-3.41, -0.03],倒置质量排序 (IMO) 的 δ CP 范围为 [-2.54, -0.32] [ 7 ]。下一代中微子振荡实验的主要物理目标,如