XiaoMi-AI文件搜索系统
World File Search System并行和分布式模拟
并行和分布式仿真领域出现于 20 世纪 70 年代和 80 年代,由两个截然不同、相互重叠的研究团体发起。一方面,并行离散事件仿真 (PDES) 团体致力于通过利用高性能计算平台来加速离散事件仿真的执行。大约在同一时间范围内,分布式仿真团体从国防团体的研究和开发工作中发展而来,该团体专注于将单独开发的仿真互连起来,这些仿真在通过局域网和广域网互连的计算机上执行。这项研究最初侧重于用于训练目的的仿真,但很快扩展到包括物理设备的分析、测试和评估等领域。虽然 PDES 和分布式仿真之间存在重要差异,但也存在许多共同的问题。在这里,我们非正式地将并行和分布式仿真描述为一个领域,它涵盖了这两个团体在从紧密耦合的并行计算平台到通过广域网连接的松散耦合机器等平台上执行单个仿真程序时出现的问题。
并行和分布式模拟
并行和分布式仿真领域出现于 20 世纪 70 年代和 80 年代,由两个截然不同、相互重叠的研究团体发起。一方面,并行离散事件仿真 (PDES) 团体关注通过利用高性能计算平台来加速离散事件仿真的执行。大约在同一时间范围内,分布式仿真团体从国防团体的研究和开发工作中发展而来,该团体专注于将通过局域网和广域网互连的计算机上执行的单独开发的仿真进行互连。这项研究最初侧重于用于培训目的的仿真,但很快扩展到包括物理设备的分析、测试和评估等领域。虽然 PDES 和分布式仿真之间存在重要差异,但也存在许多共同的问题。在这里,我们非正式地将并行和分布式模拟描述为一个领域,它涵盖了这两个社区在从紧密耦合的并行计算平台到通过广域网连接的松散耦合机器的平台上执行单个模拟程序而产生的问题。
计算机工程课程.pdf
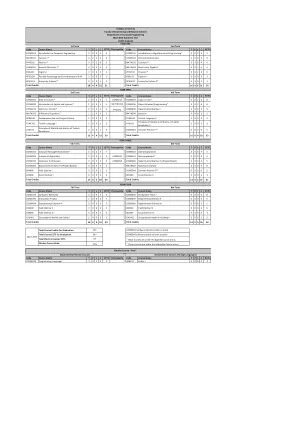
COME306 数字信号处理 3 0 0 3 5 ARB124 阿拉伯语 II 3 0 0 3 5 COME310 实时系统 3 0 0 3 5 CHN123 中文 I 3 0 0 3 5 COME311 数据安全 3 0 0 3 5 CHN124 中文 II 3 0 0 3 5 COME312 用户界面设计 3 0 0 3 5 ESP123 西班牙语 I 3 0 0 3 5 COME313 数学建模 3 0 0 3 5 ESP124 西班牙语 II 3 0 0 3 5 COME314 控制系统简介 3 0 0 3 5 FRN123 法语 I 3 0 0 3 5 COME317 智能机器人 2 0 2 3 5 FRN124 法语 II 3 0 0 3 5 COME318 计算机图形学 3 0 0 3 5 GER123 德语 I 3 0 0 3 5 COME319 移动编程 2 0 2 3 5 GER124 德语 II 3 0 0 3 5 COME324 可视化编程 2 0 2 3 5 RSN123 俄语 I 3 0 0 3 5 COME326 网络编程 2 0 2 3 5 RSN124 俄语 II 3 0 0 3 5 COME401 数据挖掘 3 0 0 3 5 COME402 人工神经网络 3 0 0 3 5 COME403 软件工程 3 0 0 3 5 COME404 模糊控制器 3 0 0 3 5 COME405 人工智能 3 0 0 3 5 COME406 并行计算 3 0 0 3 5 COME407 图像处理 3 0 0 3 5 COME408 网络安全 3 0 0 3 5 COME409 自动机理论 3 0 0 3 5 COME410 系统编程 3 0 0 3 5 COME411 系统分析与设计 3 0 0 3 5 COME412 嵌入式系统 3 0 0 3 5 COME414 优化技术 3 0 0 3 5 COME416 编译器设计 3 0 0 3 5 COME418 自然语言处理 3 0 0 3 5 COME420 生物医学和实验室仪器 3 0 0 3 5 COME422 脑机接口简介 3 0 0 3 5
考虑多尺度不确定性的电力系统容量扩张嵌套交叉分解算法
现代电力系统见证了可再生能源、储能、电动汽车和各种需求响应资源的迅速普及。因此,电力基础设施规划面临着更多挑战,因为各种新资源带来了多变性和不确定性。本研究旨在开发一个多阶段多尺度随机混合整数规划 (MM-SMIP) 模型,以捕捉电力系统容量扩张问题的粗时间尺度不确定性,例如投资成本和长期需求随机性,以及细时间尺度不确定性,例如每小时可再生能源产出和电力需求不确定性。要应用于实际电力系统,所得到的模型将导致极大规模的混合整数规划问题,不仅遭受众所周知的维数灾难,而且每个阶段的大量整数变量也会带来计算困难。针对MM-SMIP模型的此类挑战,我们提出了一种嵌套交叉分解算法,该算法由两层分解组成,即Dantzig-Wolfe分解和L形分解。该算法在我们的数值研究中表现出良好的计算性能,并且特别适合并行计算,这也将通过计算结果得到证明。
模块描述医疗系统工程
◾介绍和组织。CFD的历史发展。CFD的重要性。主方法(有限差异, - 元素, - 元素)用于离散。◾向量和并行计算。如何使用超级计算机,最佳计算循环,验证过程,最佳实践指南。◾方程式线性系统。迭代解决方案方法。示例和示例。三角形系统。实现MATLAB-SCRIPT,用于用Dirichlet-Neumann边界条件在腔(泊松方程)中使用简单流的溶液。◾融合标准和测试的选择。网格独立性。对解决方案的影响。◾根据comsol介绍有限元素。基于一个简单示例的comsol介绍和实际使用。◾执行CFD:CAD,网格产生和解决方案。网格的重要性。最佳实践(ERCOFTAC)。gambit介绍,CAD-DATA和网格的生产。网格质量。◾物理模型流利。这些模型对于获得良好解决方案的重要性。流利的简介。网格和收敛标准的影响。一阶和二阶离散化。网格依赖性。◾属性和湍流的计算。湍流建模。在向后的步骤后面的动荡流组合。为最终项目派遣主题。
Applied Digital 使用 Supermicro AI 服务器
Applied Digital 认为,最适合其用户的系统是 Supermicro SYS- 821GE-TNHR,它配备双第四代英特尔® 至强® 铂金处理器 8462Y+。这些服务器使用 NVIDIA HGX H100 GPU,每个 GPU 配备 80GB 内存。NVIDIA H100 为 HPC 提供 67 万亿次浮点运算的 FP64 Tensor Core 计算,而融合 AI 的 HPC 应用程序可以利用 H100 的 TF32 精度实现单精度矩阵乘法运算的 1 千万亿次浮点运算吞吐量。该系统在计算节点内托管八个 H100 Tensor Core GPU 和 900GB/s NVSwitch,用于 GPU 到 GPU 的通信。Applied Digital 选择 2TB 的系统 RAM 来在转移到 GPU 内存之前暂存工作负载。对于网络,Applied Digital 使用 100GbE 进行带内管理和对象存储,并使用 NDR 结构进行 GPU Direct 和融合闪存文件系统流量。利用 NVIDIA DGX 参考架构,Applied Digital 可扩展到在单个并行计算集群中工作的数千个 H100 GPU。
摘要简介
Ising模型的基态搜索可以用来解决很多组合优化问题。在目前的计算机架构下,一种适合硬件计算的Ising基态搜索算法对于解决实际问题是必不可少的。受弹簧势能转换的启发,我们提出了一种基于弹簧振动模型的点卷积神经网络基态搜索算法,即Spring-Ising算法。Spring-Ising算法将自旋看作一个连接到弹簧上的运动质点,并建立所有自旋的运动方程。Spring-Ising算法可以通过神经网络的基本结构映射到GPU或者AI芯片上,实现快速高效的并行计算。该算法对于Ising模型的求解有着非常高效的效果,已经在公认的测试基准K 2000中进行了测试。该算法引入动态平衡的概念,通过动态调整弹簧振动模型中Ising模型的权重,实现更细致的局部搜索。最后是简单的硬件测试速度评估。 Spring-Ising算法可以提供在专注于加速神经网络计算的芯片上计算Ising模型的可能性。
考虑调节服务和储能退化的随机配电系统规划方法
随着储能参与辅助服务市场的趋势,将快速变化的实时信号纳入长期配电系统规划中仍然具有繁重的计算负担。本文针对含储能的配电系统提出了一种两阶段随机规划,其中同时考虑了储能退化和频率调节的辅助服务收益。为此,将问题表述为混合整数线性规划,优化总体规划成本,包括投资和维护成本、电力交易成本和调节服务收益。在目标中加入了退化惩罚,以避免在提供调节服务时过度充电/放电,从而进一步有利于配电系统的经济性。该模型还考虑了负荷需求和电价的不确定性。采用高斯混合模型来表征这些不确定性,并抽样了一组代表性场景。为了加速优化,提出了一种改进的并行计算渐进式对冲方法。通过 33 总线配电系统证明,在 100 个场景中解决模型时,所提出的算法的速度大约是最先进的商业软件 Gurobi 的 15 倍。对于此案例研究,考虑退化惩罚已被证明可以将储能寿命延长一年。
太棒了!开发和使用瑞士军刀......
tadah!代码提供了一个多功能平台,用于开发和优化机器学习间的原子质潜力(MLIP)。通过集成综合描述符,它允许对系统交互的细微表示,并具有独特的截止函数和交互距离。tadah!支持贝叶斯线性回归(BLR)和内核脊回归(KRR),以增强模型的准确性和不确定性管理。关键特征是其超参数优化周期,迭代精炼模型体系结构以提高可传递性。这种方法结合了构图的限制,将预测与实验和理论数据保持一致。tadah!提供了一个用于LAMMP的接口,从而使MLIP在分子动力学模拟中的部署。它专为广泛的可及性而设计,支持桌面和HPC系统上的并行计算。tadah!利用模块化的C ++代码库,利用编译时间和运行时多态性来灵活性和效率。神经网络支持和预定义的粘结方案是潜在的未来发展,以及塔达!仍然对社区驱动的功能扩展开放。综合文档和命令行工具进一步简化了MLIP的开发和应用。
Microsoft Word - 2008 年 6 月 1 日带照片的新简历.doc
姓名 Kusum Deep 婚前姓 Kusum Shanker 官方地址 印度理工学院鲁尔基分校数学系副教授,鲁尔基 – 247667,印度 住宅地址 House No. 413/4, 35 – A, Civil Lines, 鲁尔基 – 247667,印度 电话 ++91 – (0) 1332-285339(办公室) ++91 – (0) 1332-275334(住宅) 手机 9837164078 传真 ++91 – (0) 1332-273560 电子邮件 kusumfma@iitr.ernet.in kusumdeep@gmail.com 官方网站http://www.iitr.ernet.in/departments/MA/people/faculty/facthtml/kusumfma.htm 出生日期 1958 年 8 月 15 日 出生地点 印度,贾朗达尔 专业 数学 数值优化技术 并行计算 教学/研究经历 研究员科学家,CBRI,鲁尔基 1988 年 6 月 15 日至 1989 年 12 月 19 日 科学家 C,CBRI,鲁尔基 1989 年 12 月 20 日至 1996 年 6 月 24 日 助理教授,数学系,印度理工学院,鲁尔基 1996 年 6 月 25 日至 2004 年 5 月 4 日 副教授,数学系,印度理工学院,鲁尔基 2004 年 5 月 5 日至今