XiaoMi-AI文件搜索系统
World File Search System振幅
概率振幅成型
在Böcherer，Steiner，Schulte [24]中提出的概率振幅成形（PAS）是一种实用结构，用于在高阶星座上与现成的前进误差校正（FEC）代码相结合的高阶星座。PA由一个分布匹配器（DM）组成，该匹配器（DM）在信号点幅度上施加了分布，然后进行系统的FEC编码，并保留幅度分配。fec编码会生成其他奇偶校验位，该位选择信号点的符号。在接收器处，FEC解码之后是逆DM。PA很快产生了很大的工业影响，尤其是在光纤通信中。该专着详细介绍了导致PAS发明的实际构想，并提供了对PAS架构的信息理论评估。由于将其分为成型层和FEC层，因此PAS的理论分析需要新工具。在塑形层上，分析了有限长度DMS的成本损失和费率损失。在FEC层上，得出了可实现的FEC速率。使用不匹配的解码，研究了可实现的速率，以解码实际重要的指标。结合了发现，这表明具有线性代码的PA在一类离散输入通道上可以实现容量。讨论了未来研究的开放问题。
量子振幅阻尼码的线性规划界限
摘要 — 鉴于近似量子纠错 (AQEC) 码的性能可能优于完美量子纠错码，因此有必要量化其性能。虽然量子权重枚举器为量子纠错码的最小距离建立了一些最佳上限，但这些上限并不直接适用于 AQEC 码。在此，我们引入了用于振幅衰减 (AD) 误差的量子权重枚举器，并在近似量子纠错框架内工作。具体而言，我们引入了代码空间固有的辅助精确权重枚举器，而且，我们在 AD 误差的量子权重枚举器和此辅助精确权重枚举器之间建立了线性关系。这使我们能够建立一个线性程序，只有当具有相应参数的 AQEC AD 码不存在时，该程序才不可行。为了说明我们的线性程序，我们在数值上排除了能够纠正任意 AD 误差的三量子比特 AD 码的存在。
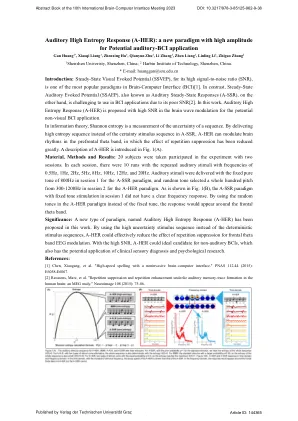
听觉高熵响应（A-HER）：潜在的听觉BCI应用程序具有高振幅的新范式
[1] Chen，Xiaogang等。“具有非侵入性大脑 - 计算机接口的高速拼写。”PNAS 112.44（2015）：E6058-E6067。 [2] Recasens，Marc等。 “重复抑制和重复增强是人脑中听觉记忆痕迹形成的基础：MEG研究。” Neuroimage 108（2015）：75-86。PNAS 112.44（2015）：E6058-E6067。[2] Recasens，Marc等。“重复抑制和重复增强是人脑中听觉记忆痕迹形成的基础：MEG研究。”Neuroimage 108（2015）：75-86。
缺口、名义应力、疲劳强度折减系数和恒定/可变振幅多轴疲劳载荷
机械组件和结构的组成结构元件具有复杂的几何形状，导致局部应力/应变集中现象。这些带缺口的结构部件经常受到随时间变化的载荷，这可能导致疲劳裂纹的产生和扩展。在非常特殊的情况下，使用中的载荷路径包括恒幅 (CA) 疲劳循环。然而，在大多数实际情况下，结构部件受到变幅 (VA) 载荷谱的影响。除此之外，疲劳设计问题进一步复杂化，因为一般来说，实际使用中的载荷历史本质上是多轴的。就受到 CA 多轴疲劳载荷的无缺口金属材料而言，对现有技术的检查表明，使用各种设计标准可以达到良好的精度水平 [1] 。然而，尽管设计可靠性如此令人鼓舞，但显然还需要做更多的工作，以便更好地将材料微观结构的影响纳入疲劳设计过程 [2] 。在此背景下，关键问题是具有不同延展性的材料对施加载荷历史的非比例性程度表现出不同的敏感性 [3] 。虽然已经进行了大量工作来研究普通金属材料的多轴疲劳行为，但迄今为止，国际科学界尚未对多轴疲劳行为进行深入研究。
皮质相位振幅耦合是发生的关键
©作者2022。由牛津大学出版社（Oxford University Press）代表大脑的担保人出版。这是根据Creative Commons Attribution-Noncmercial Licens（https://creativecommons.org/licenses/by-nc/4.0/）发行的一份开放访问文章，该媒介在任何媒介中都可以在任何媒介中进行任何媒介，但前提是原始工作被正确引用。有关商业重复使用，请联系journals.permissions@oup.com 1
通过量子振幅估计和切比雪夫插值进行百慕大期权定价
摘要 金融衍生品的定价，特别是百慕大期权等可提前行使的期权的定价，是金融机构重要但繁重的数值任务，其加速将对业务产生巨大的影响。最近，量子计算在金融问题中的应用开始被研究。在本文中，我们首次提出了一种百慕大期权定价的量子算法。该方法使用通过量子振幅估计估计出的插值节点的值，通过切比雪夫插值对百慕大期权定价的关键部分延续值进行近似。在该方法中，生成基础资产价格路径的调用预言机的次数为 O(ϵ –1)，其中 ϵ 是期权价格的误差容忍度。这意味着与基于经典蒙特卡洛的方法（如最小二乘蒙特卡洛）相比，速度提高了二次方，其中预言机调用次数为 O(ϵ –2)。
为什么在量子计算中实值振幅就足够了
需要量子计算。对于许多实际问题，仍然需要更快的计算。例如，如果我们能够处理更多数据，目前深度学习的惊人成功（参见 [2]）可能会更加惊人。计算机处理信息的能力受到限制，其中一个原因是所有速度都受光速限制。即使以光速，将信号从 30 厘米大小的笔记本电脑的一侧发送到另一侧也需要 1 纳秒 - 在此期间，即使是最便宜的当前计算机也要执行至少 4 次操作。因此，为了加快计算速度，有必要使计算机组件更小。这些组件（例如存储单元）已经由少量分子组成。如果我们将这些细胞做得更小，它们将只由几个分子组成。为了描述如此小物体的行为，有必要考虑量子物理学 - 微观世界的物理学；参见 [1, 4]。因此，计算机需要考虑量子效应。
对长期振幅漂移具有鲁棒性的量子门
量子门通常容易受到驱动门的物理量子位所施加的经典控制场的缺陷的影响。减少这种错误源的一种方法是将门分成几部分，称为复合脉冲，通常利用错误随时间的恒定性来减轻其对门保真度的影响。在这里，我们扩展了这种技术来抑制拉比频率的长期漂移，通过将它们视为幂律漂移的总和，其对状态向量的过度或不足旋转的一阶效应呈线性相加。幂律漂移的形式为 tp，其中 t 是时间，常数 p 是其幂。我们表明，抑制所有幂律漂移（p ⩽ n）的复合脉冲也是滤波器阶数为 n + 1 的高通滤波器[H. Ball 和 MJ Biercuk，《用于量子逻辑的 Walsh 合成噪声滤波器》，EPJ Quantum Technol。 2,11（2015）]。我们给出了用该技术获得的满足我们提出的幂律幅度标准 PLA(n) 的序列，并将其在时间相关幅度误差下的模拟性能与一些传统的复合脉冲序列进行了比较。我们发现，在一系列噪声频率下，PLA(n) 序列比传统序列提供更多的误差抑制，但在低频极限下，非线性效应对门保真度的影响比频率滚降更为重要。因此，先前已知的 F1 序列是 PLA(1) 标准的两个解之一，可以抑制线性长期漂移和一阶非线性效应，在低频极限下，它是比任何其他 PLA(n) 序列更清晰的噪声滤波器。
用不同分辨率模拟的太阳日珥大振幅纵向振荡
背景。近几十年来，人们对太阳日珥中的大振幅纵向振荡 (LALO) 进行了广泛的研究。然而，它们的衰减和放大机制尚不清楚。目的。在本研究中，我们使用高分辨率数值模拟研究了 LALO 的衰减和放大，空间分辨率逐渐提高。方法。我们使用包含倾角区域的二维磁配置对 LALO 进行了时间相关的数值模拟。在磁倾角中加载日珥质量后，我们通过沿磁场扰动日珥质量来触发 LALO。我们使用四个空间分辨率值进行了实验。结果。在分辨率最高的模拟中，周期与摆模型非常吻合。收敛实验表明，随着分辨率的提高，阻尼时间在底部日珥区域达到饱和，这表明振荡衰减存在物理原因。在日冕顶部，振荡在最初几分钟内被放大，然后缓慢衰减。特征时间表明在具有最高空间分辨率的实验中放大更显著。分析表明，底部和顶部日冕区域之间的能量交换是导致 LALO 衰减和放大的原因。结论。高分辨率实验在研究 LALO 的周期和阻尼机制时至关重要。只有使用足够高的空间分辨率时，周期才与摆模型一致。结果表明，在空间分辨率不足的模拟中，数值扩散可能会隐藏重要的物理机制，例如振荡放大。