XiaoMi-AI文件搜索系统
World File Search System建筑设备操作员 - 机器操作员(男/女/其他)
• 您将根据您的资历和经验在 TV AL II* 框架内获得报酬,这意味着您还将受益于节日和圣诞节奖金以及公司养老金计划和资本形成福利 • 受益于我们的内部培训和晋升机会,这为您提供了专业发展的机会 • 在国际化和包容性的工作环境中体验美国的“生活方式” • 作为我们空军大家庭的一员,美国传统的感恩节也将成为您的节日 您将通过重新分配工作时间获得额外 9 天的休息时间**
设备操作员
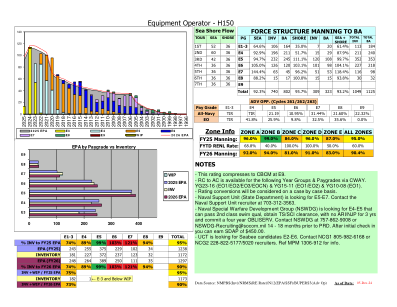
- 此等级在 E9 时压缩为 CBCM。 - 可通过 CWAY 为以下年级和薪级提供 RC 至 AC。YG23-16(EO1/EO2/EO3/EOCN)和 YG15-11(EO1/EO2)和 YG10-08(EO1)。 - 等级转换将根据具体情况考虑。 - 海军支援部队(国务院)正在寻找 E5-E7。请联系海军支援部队招聘人员,电话 703-312-3563。 - 海军特种作战发展组 (NSWDG) 正在寻找 E4-E5,能够通过二级游泳资格考试,获得 TS/SCI 许可,3 年内没有 ARI/NJP,并承诺四年的 OBLISERV。请在 PRD 前 14 - 18 个月联系 NSWDG,电话 757-862-9008 或 NSWDG-Recruiting@socom.mil。初次登记后,您可以获得 450.00 美元的 SDAP。- UCT 正在寻找 E2-E6 的海蜂候选人。请联系 NCG1 805-982-6168 或 NCG2 228-822-5177/5020 招聘人员。参考 MPM 1306-912 了解详情。
EEG录音机操作员手册EEG录音机操作员手册
目录目录的目录指示表。。。。。。。。。。。。。。。。。。。。。。。。。。4个警告。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5快速启动指南。。。。。。。。。。。。。。。。。。。。。。。。。。。7步骤1:在Ceribell EEG录音机上的功率。。。。。。。。.7步骤2:输入患者信息。。。。。。。。。。。。。。.7步骤3:连接Ceribell EEG头带。。。。。。.13步骤4:收听EEG波形。。。。。。。。。。。。。。。。.14步骤5:查看癫痫发作负担。。。。。。。。。。。。。。。。。。。。.16步骤6:停止脑电图记录。。。。。。。。。。。。。。。。。.17系统概述。。。。。。。。。。。。。。。。。。。。。。。。。。18个系统组件。。。。。。。。。。。。。。。。。。。。。。。。。。.18系统描述。。。。。。。。。。。。。。。。。。。。。。。。。。。.19充电电池。。。。。。。。。。。。。。。。。。。。。。。。。。.20在Ceribell EEG录音机上进行动力。。。。.22 Ceribell EEG录音机软件。。。。。。。。。。。。。。23主屏幕。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.23启动脑电图记录。。。。。。。。。。。。。。。。。。。。。。.24检查电极连接。。。。。。。。。。。。。。。。.26电极阻抗可听见通知。。。。。。。.27停止脑电图记录。。。。。。。。。。。。。。。。。。。。。.29添加标签和注释。。。。。。。。。。。。。。。。。。。。。。。。.30查看EEG波形。。。。。。。。。。。。。。。。。。。。。。。.31听EEG波形。。。。。。。。。。。。。。。。。。。。.32收听声音库样本。。。。。。。。。。。。。。.33观看癫痫发作负担。。。。。。。。。。。。。。。。。。。。。。。。.33连续癫痫发作通知。。。。。。。。。。。。。。。。.34扣押负担可听见通知。。。。。。。。。。。。。.34通过USB传输脑电图记录文件。。。。。。。。。.36通过WiFi传输EEG记录文件。。。。。。。。。.36默认可听见通知设置。。。。。。。。。。。。。.39设置日期/时间。。。。。。。。。。。。。。。。。。。。。。。。。。。。.41设备信息。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.41维护服务。。。。。。。。。。。。。。。。。。。。。。。。。.42 Ceribell EEG Portal。。。。。。。。。。。。。。。。。。。。。。。。。43癫痫发作检测模块。。。。。。。。。。。。。。。。。。.43癫痫发作检测模块的验证。。。。。。。.45临床性能数据。。。。。。。。。。。。。。。。。。。。。。。。。.45临床性能测试的结果。。。。。。。。。。。。。。.47结论。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.49