XiaoMi-AI文件搜索系统
World File Search System量子振幅估计案例研究
摘要。量子体积是一个全面的、单一的数字指标,用于描述量子计算机的计算能力。近年来,它呈指数级增长。在本研究中,我们将假设这种情况仍然如此,并将这一发展转化为另一种量子算法——量子振幅估计的性能发展。这是使用噪声模型完成的,该模型估计算法单次运行的错误概率。其参数与模型假设下的量子体积有关。将相同的噪声模型应用于量子振幅估计,可以将错误率与每秒生成的 Fisher 信息联系起来,这是量子振幅估计作为一种数值积分技术的主要性能指标。这为其积分能力提供了预测,并表明,如果没有重大突破,作为一种数值积分技术的量子振幅估计在不久的将来不会比传统替代方案更具优势。
STK Premium(太空)高级分析工具和... - Agi
STK 的 SatPro 功能可实现更高保真度的卫星系统建模和分析。SatPro 中包含的传播器可以整合数值积分和运动微分方程、计算月和年的星历表,并集成专门的传播方法。SatPro 还通过姿态范围、姿态覆盖以及定制的配置文件和约束增强了设计师和操作员的姿态分析。最后,SatPro 为您提供了一组卫星工程工具,用于模拟卫星的表面积、质量、太阳能电池板配置等。
智能材料系统和 MEMS
7 有限元法简介 145 7.1 简介 145 7.2 变分原理 147 7.2.1 功和补充功 147 7.2.2 应变能、补充应变能和动能 148 7.2.3 加权残值技术 149 7.3 能量泛函和变分算子 151 7.3.1 变分符号 153 7.4 控制微分方程的弱形式 153 7.5 一些基本能量定理 154 7.5.1 虚功的概念 154 7.5.2 虚功原理(PVW) 154 7.5.3 最小势能原理(PMPE) 155 7.5.4 Rayleigh-Ritz 方法 156 7.5.5 Hamilton 原理(HP) 156 7.6 有限元法 158 7.6.1 形函数 159 7.6.2 有限元方程的推导 162 7.6.3 等参公式和数值积分 164 7.6.4 数值积分和高斯求积 167 7.6.5 质量和阻尼矩阵公式 168 7.7 有限元法中的计算方面 171 7.7.1 影响 FE 解速度的因素 172 7.7.2 静态分析中的方程解 173 7.7.3 动态分析中的方程解 174 7.8 超收敛有限元公式 178 7.8.1 超收敛深杆有限元 179 7.9 谱有限元公式 182 参考文献 184
智能材料系统和 MEMS
7 有限元法简介 145 7.1 简介 145 7.2 变分原理 147 7.2.1 功和补充功 147 7.2.2 应变能、补充应变能和动能 148 7.2.3 加权残值技术 149 7.3 能量泛函和变分算子 151 7.3.1 变分符号 153 7.4 控制微分方程的弱形式 153 7.5 一些基本能量定理 154 7.5.1 虚功的概念 154 7.5.2 虚功原理(PVW) 154 7.5.3 最小势能原理(PMPE) 155 7.5.4 Rayleigh-Ritz 方法 156 7.5.5 Hamilton 原理(HP) 156 7.6 有限元法 158 7.6.1形函数 159 7.6.2 有限元方程的推导 162 7.6.3 等参公式和数值积分 164 7.6.4 数值积分和高斯求积 167 7.6.5 质量和阻尼矩阵公式 168 7.7 有限元法中的计算方面 171 7.7.1 影响 FE 解速度的因素 172 7.7.2 静态分析中的方程解 173 7.7.3 动态分析中的方程解 174 7.8 超收敛有限元公式 178 7.8.1 超收敛深杆有限元 179 7.9 谱有限元公式 182 参考文献 184
教授英语。 ANDREA PANTEGHINI 博士- 布雷西亚
• 2011-2012 至 2014-2015 学年担任建筑工程专业材料与结构力学 (A. Carini 教授) 助教 • 2011-2012 学年担任计算非线性力学 (A. Salvadori 教授) 课程中的塑性本构模型数值积分研讨会。 • 2012-2013 学年担任计算非线性力学 (L. Bardella 教授) 助教。 • 2012-2013 学年和 2013-2014 学年结构动力学 (A. Feriani 教授) 助教 • 2014-2015 学年布雷西亚大学结构动力学兼职教授 • 2015-2016 学年至 2022-2023 学年布雷西亚大学材料与结构力学兼职教授 • 2019-2020 学年至 2021-2022 学年布雷西亚大学基础课程计算岩土力学模块教师。 • 2022-2023 学年布雷西亚大学计算非线性结构力学计算塑性模块教师。 • 自 2022-2023 学年起担任布雷西亚大学材料与结构力学教授,指导博士生
数值积分的通用量子算法
量子算法已在诸多应用领域展现出优越性,然而数值积分这一处理复杂科学与工程问题不可或缺的工具,却一直缺乏通用的量子算法。本文,我们首次提出了一种适用于任意能用多项式近似的连续函数的量子积分算法,该算法通过多项式近似实现对任意可积函数的量子编码,然后构造量子预言机标记积分区域内的点数,最后将统计结果转化为叠加态振幅中的相角。本文提出的量子算法比经典积分算法具有二次加速效果,计算复杂度从O(N)降低到O(√N)。我们的工作解决了提高量子积分算法通用性的关键障碍,为拓展量子计算的优越性提供了有意义的指导。
船舶性能原理课程笔记 - 海军学院
目录 I. 介绍 课程政策 方程式和换算因子 符号和缩写 II. 课程笔记 第 1 章:工程基础知识 第 2 章:船体形状和几何形状 第 3 章:流体静力学 第 4 章:稳定性 第 5 章:海军材料的特性 第 6 章:船舶结构 第 7 章:船舶阻力和动力 第 8 章:耐波性 第 9 章:船舶操纵性 第 10 章:潜艇和潜水器 III. 附录 附录 A:淡水和咸水密度表 附录 B:淡水和咸水运动粘度表 附录 C:常见几何形状的性质 IV.船舶数据部分(形状曲线和完整稳定性的交叉曲线) FFG 7 级 CVN 65 级 DDG 51 级(Flt II/IIA) AOE 6 级 LCS 1 级 USNA 船厂巡逻(新)27-B-1 水文实验室模型 V. 实验室讲义 实验室 1:数值积分 实验室 2:阿基米德和浮心 实验室 3:倾斜实验 实验室 4:复原力臂 - 重心的垂直和横向移动 实验室 5:自由表面效应和损伤稳定性 实验室 6:材料和材料测试 实验室 7:船体阻力和有效马力 实验室 8:螺旋桨演示 实验室 9:耐波性
周期驱动的两能级系统的相位因子
对与周期性或准周期性时间相关外部源相互作用的力学系统(经典或量子)的行为进行理论计算,需要对其在长时间内的行为进行非常好的控制。简单的解决方法可能会导致涉及长期项(依赖于时间的多项式增长项)或小分母(特别是在准周期相互作用下)的棘手问题。通常的数值积分方法在长时间内也可能不稳定,并会导致不受控制的误差。这些问题最早是在天体力学中发现的,在周期性或准周期时间相互作用下的物理系统中普遍存在。这些稳定性问题及其解决方案的分析是物理学和应用数学的一个广泛研究领域,并导致了重要的发展,如庞加莱-林德斯泰特级数和 KAM 理论。此类系统的微扰处理的主要目标是用依赖于时间的均匀收敛级数来表达物理上有意义的量,也就是说,用级数来表达,当截断时,与精确解的差异最多为一个固定的微小量,并且不会随时间而增加。量子相的计算是一种相关的物理情况,其中这种均匀的,即时间
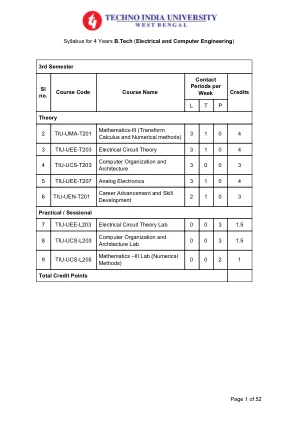
4 年制 B.Tech(电气和计算机)课程大纲...
详细课程大纲 第一单元:变换微积分拉普拉斯变换:拉普拉斯变换、性质、逆、卷积、用拉普拉斯变换求某些特殊积分、初值问题的解。傅里叶级数:周期函数、函数的傅里叶级数表示、半程级数、正弦和余弦级数、傅里叶积分公式、帕塞瓦尔恒等式。傅里叶变换:傅里叶变换、傅里叶正弦和余弦变换。线性、缩放、频移和时移性质。傅里叶变换的自互易性、卷积定理。应用于边界值问题。第二单元:数值方法近似和舍入误差、截断误差和泰勒级数。插值 - 牛顿前向、后向、拉格朗日除差。数值积分 - 梯形、辛普森 1/3。通过二分法、迭代法、牛顿-拉夫森法、雷古拉-法尔西法确定多项式和超越方程的根。通过高斯消元法和高斯-西德尔迭代法求解线性联立线性代数方程。曲线拟合-线性和非线性回归分析。通过欧拉法、修正欧拉法、龙格-库塔法和预测-校正法求解初值问题。
噪声量子计算机上的量子振幅估计
[1] G. Brassard 等人。量子振幅放大与估计。当代数学,305:53–74,2002。[2] Y. Suzuki 等人。不带相位估计的振幅估计。量子信息处理,19(2):75,2020。[3] S. Aaronson 和 P. Rall。量子近似计数,简化。在算法简单性研讨会上,第 24-32 页。SIAM,2020 年。[4] D. Grinko 等人。迭代量子振幅估计。arXiv 预印本 arXiv:1912.05559,2019。[5] K. Nakaji。更快的振幅估计。 arXiv preprint arXiv:2003.02417,2020 年。[6] R. Venkateswaran 和 R. O'Donnell。具有非自适应 Grover 迭代的量子近似计数,2020 年。[7] DS Abrams 和 CP Williams。用于数值积分和随机过程的快速量子算法。arXiv preprint quant-ph/9908083,1999 年。[8] A. Montanaro。蒙特卡罗方法的量子加速。英国皇家学会学报 A:数学、物理和工程科学,471(2181):20150301,2015 年。[9] P. Rebentrost、B. Gupt 和 TR Bromley。量子计算金融:金融衍生品的蒙特卡罗定价。 Physical Review A, 98(2):022321, 2018. [10] S. Woerner 和 DJ Egger. 量子风险