XiaoMi-AI文件搜索系统
World File Search System亚历山大·哈特迈尔的简历 - FRASCAL
Alexander Hartmaier 博士目前是德国波鸿鲁尔大学材料科学教授(材料力学系主任)和先进材料模拟跨学科中心 (ICAMS) 主任,负责微观力学和宏观建模系。自 2016 年起,他担任哈尔滨工业大学的客座教授,2016 年至 2019 年为蒋江学者项目成员。2005 年 11 月至 2008 年 5 月,他担任德国埃尔朗根-纽伦堡弗里德里希亚历山大大学材料科学教授。在此之前,他曾领导德国斯图加特马克斯普朗克金属研究所高华建教授“介观现象理论”系“纳米结构材料”小组。他也曾在该研究所完成博士论文,该论文于 2000 年荣获马克斯·普朗克学会奥托·哈恩奖章。在斯图加特马克斯·普朗克研究所任职期间,Hartmaier 博士曾以项目负责人和小组负责人的身份从事了三年的工业研究。他的研究工作重点是异质材料变形、断裂和疲劳的微观机械和尺度桥接建模,以及最近的数据导向方法和机器学习在材料科学中的应用。除了学术活动之外,Hartmaier 博士还担任德国材料学会德国材料学会 (DGM) 主席(2017/18 年度)、董事会成员(2013 年至 2018 年)以及青年科学家计划发言人(2011 年至 2014 年)。
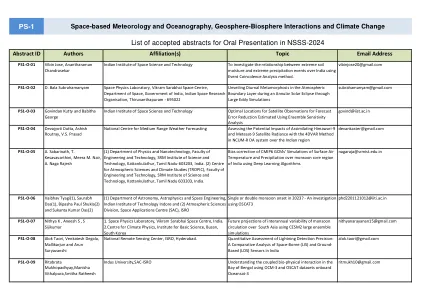
NSSS-2024中的口头演示摘要清单
(1)印度太空研究组织的空间应用中心,印度艾哈迈达巴德(2)以前在印度蒂鲁瓦南塔布拉姆(Thiruvananthapuram)695022的Vikram Sarabhai太空中心,印度太空和大气科学司,印度艾哈迈德巴德(4)TC 95/1185/1185,kumaraa,kumaraa,kumaraa,kumaraa,印度印度蒂鲁瓦南塔普兰(Thiruvananthapuram),印度海得拉巴,印度海得拉巴国家遥感中心(6)空间物理实验室,维克拉姆·萨拉巴海(Vikram Sarabhai)空间中心,印度蒂鲁瓦南塔普拉姆(Thiruvananthapuram),印度蒂鲁瓦南塔普兰(7)大气化学系,马克斯·普朗克化学部,麦克斯·普朗克化学研究所,麦克斯(Max Planck
绝热量子计算机上圈量子引力模拟的前奏
本文讨论了在绝热量子计算机上实现自旋网络状态的可能性,该状态用于环量子引力方法中的普朗克尺度物理。讨论的重点是应用当前可用的技术,并分析了 D-Wave 机器的一个具体示例。介绍了一类简单的自旋网络状态,可以在 D-Wave 量子处理器的 Chimera 图架构上实现。然而,需要超越当前可用的量子处理器拓扑来模拟更复杂的自旋网络状态。这可能会启发新一代绝热量子计算机。讨论了模拟环量子引力的可能性,并提出了一种使用绝热量子计算解决图不变标量(哈密顿)约束的方法。所提出的结果为未来在量子退火器上模拟普朗克尺度物理,特别是量子宇宙学配置奠定了基础。
量子引力以暗粒子形式局部大规模激发
我们渐近地构造了一个静态球形激发态,该激发态在可重正化量子引力中无奇点,具有无背景性质。其直径由量子引力的关联长度给出,比普朗克长度长 2 个数量级,外部有史瓦西尾。内部的量子引力动力学采用非微扰高阶修正表达式来描述,该表达式假设了动力学在强耦合的边缘消失的物理要求。运行耦合常数是非线性和非局域性的表现,通过将其近似为依赖于径向坐标的平均场来管理。如果质量是普朗克质量的几倍,我们可以建立一个包含运行效应的引力势线性化运动方程组,并获得激发态作为其解。它可能是暗物质的候选者,并将为黑洞物理学提供新的视角。
简短简历
Stergios Logothetidis 于 1977 年获得塞萨洛尼基亚里士多德大学 (AUTH) 物理学学位,1980 年获得电子学硕士学位,1983 年获得 AUTH 物理系博士学位。随后,他于 1983 年至 1985 年在斯图加特马克斯普朗克研究所 (MPI) 担任博士后研究员,1985 年在 MPI 担任研究员,1988 年至 1989 年在柏林 BESSY 同步辐射实验室工作。他曾获得德国亚历山大·冯·洪堡基金会和马克斯普朗克研究所的研究员奖学金。此外,他还因完成博士论文而获得奥纳西斯基金会的研究员奖学金,因在研究生学习期间表现出色(排名第一)而获得 OTE 奖学金,并在整个本科学习期间获得国家奖学金基金会(排名第一)。荣获“希腊文学家协会”精神、艺术、科学和社会价值先驱者颁奖典礼上的荣誉奖和奖状。
量子引力中的幺正性和信息
在量子引力方法中,平滑时空是离散普朗克基本结构的近似,任何有效的平滑场理论描述都会遗漏部分基本自由度,从而破坏幺正性。这也适用于通过使用闵可夫斯基背景几何实现的平凡引力场(低能)理想化,与任何其他时空几何一样,在基本描述中,它对应于无数个不同且紧密退化的离散微观状态。这种微观状态的存在为黑洞蒸发结束时要编码的信息提供了巨大的 q 位储存库,从而为黑洞蒸发信息难题的自然解决开辟了道路。在本文中,我们表明,这些预期可以在由圈量子引力激发的宇宙学简单量子引力模型中精确实现。具体而言,即使模型基本上是单一的,当适当忽略与低能宇宙观察者无关的微观自由度时,有效描述中的纯态也会由于与普朗克微观结构的退相干而演变为混合态。此外,在相关的物理范围内,这些隐藏的自由度不携带任何“能量”,因此在完全量子引力的背景下实现了退相干可以在不耗散的情况下发生的想法(Unruh 和 Wald 之前强调过),现在在一个由量子引力强烈推动的具体引力模型中。所有这些都强化了黑洞蒸发难题的一个相当保守和自然的解决方案的观点,其中信息不会被破坏,而只是被降级(低能观察者无法获得)为与普朗克尺度量子几何的微观结构的相关性。
人工智能
德国的人工智能研究主要在大学进行,但也在大学以外的研究机构进行。德国研究基金会 (DFG) 是支持人工智能研究的主要资助机构。重要的德国研究组织,如弗劳恩霍夫学会 (应用研究)、莱布尼茨学会 (基础和应用研究) 和马克斯普朗克学会 (基础研究) 都拥有自己的研究机构,主要关注人工智能。一些人工智能研究机构和项目由联邦和州政府直接资助。还有一些私人和公共基金会支持德国的人工智能研究,例如亚历山大冯洪堡基金会 (AvH)。研究生培训由大学和非大学研究机构与大学合作提供。除了 DFG 之外,亥姆霍兹联合会 (重大挑战研究) 和马克斯普朗克学会也提供人工智能研究或与人工智能研究密切相关的研究生培训计划。此外,还设有由州政府、德国学术交流中心 (DAAD) 和基金会提供的博士学位课程和博士学位资助。
量子重力,最小长度和全息
摘要。karolyhazy的不确定性关系指出,如果使用设备测量长度L,则测量中将有最小的不确定性δl,由(δl)3〜l 2 p l给出。这是结合量子力学原理和一般相对论的结果。在这封信中,我们表明了这种关系是如何以自下而上的方式,从时空 - 时间 - 物质原子的基质动力学来产生的。我们使用这种关系来定义Planck量表的空间 - 时间 - 物质(STM)泡沫,并认为我们的理论是全息的。通过比普朗克时间大的时间尺度上的粗粒子,获得了量子重力定律。量子重力不是普朗克量表现象;相反,每当经典时空背景都无法描述量子系统时,它就会发挥作用。空间时间和经典相对论是由高度纠缠的量子重力系统中的自发定位引起的。karolyhazy的关系继续存在于新兴理论中。这种关系的实验确认将构成重力量子性质的定义测试。
利用 AMDirT 促进古代宏基因组数据的可访问、快速和适当的处理
1 莱布尼茨天然产物研究和感染生物学研究所汉斯·诺尔研究所“微观宇宙平衡”卓越集群,阿道夫·赖希魏因大街 23 号,耶拿,图林根州,07745,德国 2 马克斯·普朗克进化人类学研究所考古遗传学系,Deutscher Pl. 6,莱比锡,萨克森州,04103,德国 3 动物学系,乌普萨拉大学,Norbyvägen 18D,乌普萨拉,752 36,瑞典 4 考古遗传学相关研究组,莱布尼茨天然产物研究和感染生物学研究所 Hans Knöll 研究所,Adolf-Reichwein-Straße 23,耶拿,图林根州,07745,德国 5 古生物技术系,莱布尼茨天然产物研究和感染生物学研究所 Hans Knöll 研究所,Adolf-Reichwein-Straße 23,耶拿,图林根州,07745,德国 6 比较生物医学和食品科学系,帕多瓦大学,Viale dell'Università 16,Legnaro,帕多瓦,350250,意大利 7 分子生态学科和进化,全球研究所,健康与医学科学学院,哥本哈根大学,Øster Farimagsgade 5,哥本哈根 K,1353,丹麦 8 约克大学考古系 BioArCh,英国约克,YO10 5DD,英国 9 传播、感染、多样化和进化小组,马克斯普朗克地质人类学研究所,Kahlaische Str. 10,耶拿,图林根,07745,德国 10 哥本哈根大学健康与医学科学学院全球研究所全基因组学系,Oester Voldgade 44747,哥本哈根 K,1350,丹麦 11 莱顿大学考古科学系,Einsteinweg 2,莱顿,2333 CC,荷兰 12 耶拿弗里德里希席勒大学生态与进化研究所,耶拿,图林根,07743,德国 13 巴黎大学巴斯德研究所微生物古基因组学部门,CNRS UMR 2000,Rue du Docteur Roux 25-28,巴黎,法兰西岛,F-75015,法国 14 马克斯普朗克-哈佛研究中心古地中海考古学 (MHAAM),马克斯普朗克进化人类学研究所,Deutscher Pl. 6,莱比锡,萨克森州,04103,德国 15