XiaoMi-AI文件搜索系统
World File Search System分子相互作用。但是有多强大和多少?
图1分子相互作用的定性相互作用,生化和定量相互作用描述。在左图上,显示了“分子A”的虚构相互作用网络,表明六个分子,其中分子B – E基于定性相互作用测量值可检测到。所有这些相互作用,即使是在第一个面板中不显示为粘合剂的相互作用,都可以用一组固有的结合常数来描述,如中间面板中的例证。这种固有的生物物理结合常数构成了亲和力相互作用,如右图在左图中所示的相同相互作用网络上所示。定量亲和力相互作用曲线立即实现了观察到的相互作用的排名,而简单的定性相互作用网络图是不可能的。此外,定量测定的检测阈值比定性相互作用分析的“结合阈值”更好地定义,从而提高了相互作用的可重复性和可靠性。
欧洲的本地电池价值链 - 宣布的政治支持有多强?
在全球清洁技术参与者的工业化补贴越来越多,欧盟逐渐被迫开发激励和安全机制,以保持其在未来技术中的优势。2022年从2022年开始的《水平减少法》(IRA)导致了与可再生有关工业的全球景观中的显着破坏。奖励国内采购和生产努力的供求方面的税收抵免模型显着推动了美国新的本地化和工业化公告。的优先事项正在转移,并且正在对投资进行重新认可,以依靠美国作为为西部市场服务的基础。同时,涉及中国和俄罗斯的地缘政治不安全感和紧张局势表明,有必要建立安全可靠的供应链,特别是考虑到仍然见证了这些国家的关键原材料的中心依赖。
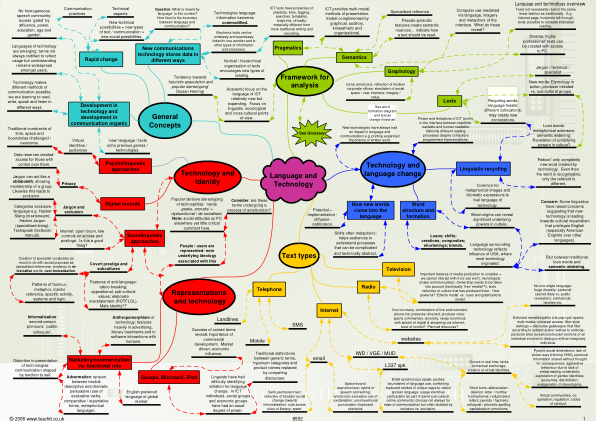
语言与技术通用...
需要考虑的媒体制作的重要特征 = 我们无法与其互动(或者我们可以吗?);独白(大众传播);需要考虑所有权(技术上“免费”媒体?);文本反映了产生它们的文化。有多强大?“效果模式”与“使用和满足模式”。
第二阶段:克服内部抑制剂
大多数犯有性犯罪的人都知道它在社会上是不可接受的,知道它是有害的,或者将担心他们将被抓获和逮捕。无论对儿童进行性虐待的动机有多强大,罪犯都必须克服其“良心”或内部抑制剂,以便进入损害儿童的下一阶段。有些人会为其行为及其后果找借口;也许吸毒或用酒精来克服恐惧或良心;或将虐待归咎于孩子的行动或愿望。
论经济自由与经济增长的关系
人们通常认为文化规范和制度可以解释为什么某些国家变得富裕而其他国家仍然贫穷(Landes,1998)。在这方面,一个重要的问题是经济自由的作用。经济发展和经济自由之间有什么联系?如果有的话。自由主义者认为,社会主义和旧的国家主导的进口替代发展模式的消亡将为保持或实现经济自由的国家带来更快、更持续的增长。另一些人则认为,如果明智地运用国家控制,可以促进增长。这场辩论一直受到两件事的困扰。首先,缺乏对经济自由的明确定义以及如何衡量它。其次,缺乏在足够广泛的国家和足够长的时间内应用这一定义的数据,无法可靠地检验自由和繁荣之间是否存在相关性。在过去十年左右的时间里,这种情况逐渐发生了变化。许多经济自由指标已经出现,随后它们被应用于实证增长模型中。到目前为止,我们缺少的是对这些指标的彻底比较和评估。这是本文的首要目标。我们关注最近引起广泛关注的两个指标,即弗雷泽研究所的指标和传统基金会的指标(华尔街日报)。选择这些指标的原因是它们适用于许多国家,并且具有可比性。虽然我们关注这些指标,但在回顾文献时,我们也会提到其他尝试。第二个目标是回顾和扩展经济自由与经济发展之间关系的经验证据。这里的一个严重问题是,经济理论没有为正确指定经验模型提供足够的指导。因此,Leamer 1983 和 Levine 和 Renelt 1992 的所谓极端 Ž . Ž . 界限分析通常用于检查感兴趣的变量(在我们的例子中是 Ž . 经济自由的衡量标准)与经济增长之间的关系有多强。 Sali-i-Martin 1997 最近指出,极端边界分析中应用的检验太强,任何变量都无法真正通过。Sali-i-Martin 建议分析整个分布,而不是分析特定变量系数估计值的极端边界。他得出结论,实证增长文献中出现的图景并不是我们通过极端边界分析得到的悲观的“没有什么是稳健的”。相反,他发现可以发现大量变量与增长密切相关。本文将这两种方法应用于经济自由与经济增长之间的关系。本文的其余部分结构如下。第 2 节讨论了我们关注的指标内容,第 3 节展示了它们之间的相关性。第 4 节回顾了先前关于经济自由度与经济增长之间关系的研究,第 5 节介绍了我们的估算结果。最后一节给出了一些总结性评论。
关联玻色子量子场多模态的纠缠和光学非经典性
有几种方法可以质疑物理系统状态的具体量子力学特性。首先,人们可能会问它的相干性有多强。量子态相干叠加的存在是物质波干涉现象的起源,因此,这是一个典型的量子特征,对此提出了几种测量和证据(有关最近的综述,请参阅 [1])。其次,当所研究的系统是二分或多分系统时,其组成部分的纠缠是另一个内在的量子特征。有大量文献探讨了各种测量方法来量化给定状态中包含的纠缠量 [2–14]。最后,对于玻色子量子场的模式,出现了第三种非经典性概念,通常称为光学非经典性。根据格劳伯的观点,光场的相干态(及其混合态)被视为“经典”,因为它们具有正的格劳伯-苏达山 P 函数 [15]。从那时起,多年来人们开发了多种光学非经典性测量方法,以测量与光学经典状态的偏离 [15–41]。光场量子态的这三种不同的、典型的量子属性被认为可作为量子信息或计量学的资源 [38, 39, 42–44]。那么自然而然地就会出现一个问题:这些属性之间有着什么样的定量关系。例如,在 [45] 中,给出了使用非相干操作从具有给定相干度的状态中可以产生多少纠缠的界限:这将相干性与纠缠联系起来。在 [46] 中,状态的相干性和光学非经典性被证明是相互关联的:远对角线密度矩阵元素 ρ ( x, x ′ ) 或 ρ ( p, p ′ ) 的显著值(称为“相干性”)是状态的光学非经典性的见证。我们的目的是建立多模玻色子场的光学非经典性和二分纠缠之间的关系。直观地看,由于所有光学经典态都是可分离的,因此强纠缠态应该是强光学非经典态。相反,仅具有弱光学非经典性的状态不可能高度纠缠。为了使这些陈述精确且定量,我们需要测量纠缠度和光学非经典性。作为评估二分纠缠的自然指标,我们使用形成纠缠 (EoF) [4]。关于光学非经典性,我们使用最近引入的单调性 [38, 39],我们将其称为总噪声单调性 ( M TN )。它是通过将纯态上定义的所谓总噪声∆x2+∆p2扩展到混合态(通过凸屋顶结构,参见(1))得到的,对于该值来说,它是光学非经典性的一个完善的量度[38–41]。我们的第一个主要结果(定理 1 和 1')在于,对于 n = n A + n B 模式的二分系统的任意状态 ρ,EoF(ρ) 关于 M TN (ρ) 的函数有一个上限。特别地,当 n A = n B = n/ 2 时,这个上限意味着包含 m 个纠缠比特的状态必须具有光学非经典性(通过 M TN 测量),并且该光学非经典性随 m 呈指数增长。作为应用,我们表明,当可分离纯态撞击平衡光束分束器时可以产生的最大纠缠度由该状态的光学非经典性的对数所限制,通过 M TN 测量。换句话说,虽然众所周知分束器可以产生纠缠 [28, 47, 48],但纠缠量受到本态光学非经典性程度的严重限制。定理 1 和 1' 中的界限可以很容易地计算出纯态的界限,因为 EoF 与还原态的冯·诺依曼熵相重合,而 M TN 与总噪声相重合。然而,对于混合态,界限与两个通常难以评估的量有关。我们的第二个主要结果(定理 2)解决了这个问题