XiaoMi-AI文件搜索系统
World File Search System酒精征费
i。 Terūnangao toa rangatira:Tamariki至Mokopuna(TTM)计划与Porirua的27名Rangatahi年龄在Porirua的14-24岁的Rangatahi组合,他们在12个月的时间内受到酒精的不利影响,以制定和/或实现个人和/或专业发展计划。该计划已经提供了20次支持会议,并具有很高的参与度和保留率。它已经开展了团队建设活动,基于NOHO的计划日,Marae旅行和社区活动。II。 e tipu e Rea:FASD(胎儿酒精谱系障碍)可能是新西兰的非遗传智力障碍的主要可预防原因,估计有76,922人患有FASD。 2酒精对发育中的身体和大脑造成的伤害塑造了受影响的人的生命。 这笔赠款允许E Tipu e Rea雇用两个年轻的Māmā来设计,交付和实施年轻的父母和酒精计划。 该计划包括与FASD和酒精危害部门的网络,以及年轻的父母创建七个动画故事,与国家媒体互动,并制定社交媒体策略,以提高对酒精对Tamariki和Rangatahi造成的代际危害的认识,并将Whānau直接为他们提供的服务。II。e tipu e Rea:FASD(胎儿酒精谱系障碍)可能是新西兰的非遗传智力障碍的主要可预防原因,估计有76,922人患有FASD。2酒精对发育中的身体和大脑造成的伤害塑造了受影响的人的生命。这笔赠款允许E Tipu e Rea雇用两个年轻的Māmā来设计,交付和实施年轻的父母和酒精计划。该计划包括与FASD和酒精危害部门的网络,以及年轻的父母创建七个动画故事,与国家媒体互动,并制定社交媒体策略,以提高对酒精对Tamariki和Rangatahi造成的代际危害的认识,并将Whānau直接为他们提供的服务。
- 韦尔斯 - 征氢.pdf
一般数据保护法规(GDPR)威尔士政府将成为您提供的任何个人数据的数据控制器,这是您对咨询的回应的一部分。威尔士部长拥有法定权力来处理此个人数据,这将使他们能够就如何行使公共职能做出明智的决定。威尔士政府工作人员将全面看到您发送的任何回应,以应对本次咨询或计划未来咨询的问题。如果威尔士政府对咨询回应进行进一步分析,则可以委托这项工作由认可的第三方进行(例如研究组织或咨询公司)。任何此类工作只能根据合同进行。威尔士政府对此类合同的标准条款和条件,规定了对个人数据处理和保管的严格要求。
本征态热化假说回顾
本论文探讨了本征态热化假说 (ETH),这是理解孤立量子系统中热行为出现的基石概念。这项工作首先通过遍历性建立经典热化的基础,其中系统会随时间探索所有可访问的微观状态。这个类比为理解 ETH 如何将这个概念转化为量子领域奠定了基础。按照 Mark Srednicki 概述的方法,论文深入研究了 ETH 的核心公式。然后,通过分析波函数、可观测量和它适用的系统类型的限制,研究了对 ETH 的限制。介绍了随机矩阵理论 (RMT) 的讨论,探讨了它与 ETH 的联系及其在通过 Wigner-Dyson 分布理解混沌量子系统中能谱的统计特性方面的作用。此外,论文还探讨了 Berry 猜想,该猜想揭示了大型量子系统中本征态的混沌性质,进一步支持了 ETH 的基本原理。最后,讨论了支持 ETH 有效性的实验,特别是冷原子气体实验。通过回顾 ETH、其理论基础以及其与 RMT 和 Berry 猜想等相关概念的联系,本论文为寻求了解孤立量子系统中热行为出现的学生提供了宝贵的资源。
了解牙周病原体三联征
3. Lourenço TGB、Heller D、Silva-Boghossian CM、Cotton SL、Paster BJ、Colombo APV 等。牙周健康和患病患者的微生物特征谱。临床牙周病学杂志。2014;41(11):1027-36。4. Arora N、Mishra A、Chugh S。微生物在牙周炎中的作用:我们到达顶峰了吗?除了红色复合体之外,还有一些未被发现的细菌。印度牙周病学会杂志。2014;18(1):9-13。5. Belibasakis GN、Belstrøm D、Eick S、Gursoy UK、Johansson A、Könönen E 等。牙周微生物学和牙周病的微生物病因:历史概念和当代观点。牙周病学 2000。 2023;第 1-17 页。6. Socransky SS、Haffajee AD。牙周微生物生态学。牙周病学。2000;38(1):135-87。7. Mohanty R、Asopa S、Joseph M、Singh B、Rajguru J、Saidath K 等人。红色复合体:口腔菌群中的多微生物聚集体:综述。家庭医学初级护理杂志。2019;8(11):3480-6。8. Shaikh HM、Patil S、Pangam T、Rathod K。多微生物协同作用和菌群失调:概述。印度牙周病学会杂志。2018;22(2):101-6。 9. Joshi V、Bhat K、Kugaji M、Ingalgi P。印度慢性牙周炎患者和牙周健康成人中伴放线杆菌的出现情况。印度牙周病学会杂志。2016;20(2):141-4。10. Holt SC、Kesavalu L、Walker S、Genco CA。牙龈卟啉单胞菌的毒力因子。牙周病学。1999;20:168-238。11. Slots J、Listgarten MA。牙龈拟杆菌、中间拟杆菌和伴放线杆菌与人类牙周病的关系。临床牙周病学杂志。1988;15(2):85-93。 12. Potempa J、Sroka A、Imamura T、Travis J。牙龈卟啉单胞菌的主要半胱氨酸蛋白酶和毒力因子:多域蛋白复合物的结构、功能和组装。Curr Protein Pept Sci。2003;4(6):397-407。13. Mayrand D、Grenier D。外膜囊泡的生物活性。Can J Microbiol。1989;35(6):607-13。14. Mihara J、Holt SC。从牙龈卟啉单胞菌W50中分离的成纤维细胞活化因子的纯化和表征。Infect Immun。1993;61(2):588-95。15. Mihara J、Yoneda T、Holt SC。牙龈卟啉单胞菌衍生的成纤维细胞活化因子在骨吸收中的作用。感染免疫。1993;61(8):3562-4。16. Onishi S、Honma K、Liang S、Stathopoulou P、Kinane D、Hajishengallis G 等人。Tannerella forsythia 亮氨酸富集重复蛋白 BspA 在牙龈上皮细胞中表达 Toll 样受体 2 介导的白细胞介素 8。感染免疫。2008;76(1):198-205。17. Armitage GC、Dickinson WR、Jenderseck RS、Levine SM、Chambers DW。龈下螺旋体百分比与牙周病严重程度的关系。牙周病学杂志。 1982;53(9):550–6。 18. Honma K、Inagaki S、Okuda K、Kuramitsu HK、Sharma A。连翘胞外多糖合成操纵子在生物膜发育中的作用。微生物病原体。 2007;42(4):156–66。 19. Socransky SS、Haffajee AD、Cugini MA、Smith C、Kent RL。龈下牙菌斑中的微生物复合体。临床牙周病学杂志。1998;25(2):134-44。20. Hajishengallis G. 牙周炎:从微生物免疫颠覆到全身炎症。自然免疫学评论。2015;15(1):30-44。21. Lamont RJ、Koo H、Hajishengallis G. 口腔微生物群:动态群落和宿主相互作用。自然微生物学评论。2009;16(12):745-59。22. Chakar C、Menassa G、Khayat R. 牙周微生物组第一部分:文献综述。国际阿拉伯牙科杂志。2021;12(1):41-7。23. Priyadharsini JV。通过计算机模拟验证非抗生素药物对乙酰氨基酚和布洛芬作为抗红色复合病原体的抗菌剂。《牙周病学杂志》。2019;90(12):1441-8。24. Ushanthika T、Girija ASS、Paramasivam A、Priyadharsini JV。通过计算机模拟方法识别利血平靶向的红色复合病原体中的毒力因子。《天然产物研究》。2021;35(11):1893-8。25. Maheaswari R、Kshirsagar J、Lavanya N。聚合酶链反应:牙周病学的分子诊断工具。《印度社会科学杂志》
eSia征用纸序列 - VII。 ...
[10]挪威EPD基金会。NPCR建筑产品和服务A部分(2017年4月),NPCR 029 B部分用于建筑物和建筑行业中使用的光伏模块,包括生产细胞,晶圆,Ingot Block,太阳能硅,太阳能硅,太阳能基质,太阳能超级材料和其他太阳能级别级别级别级别级别级别级别材料1.2版1.2版(3月,20222年3月)。也由国际EPD®系统作为C-PCR-016光伏模块及其零件(2022年4月)采用。
时空量子参考系和本征时叠加
在广义相对论中,时空的描述依赖于理想化的杆和时钟,它们确定了一个参考系。在任何具体场景中,参考系都与物理系统相关联,而物理系统最终是量子的。因此,物理定律的相对论描述需要考虑这样的量子参考系 (QRF),通过它们可以赋予时空以操作意义。在这里,我们引入了时空量子参考系的概念,它与时空中的量子粒子相关联。这种表述的优点是将空间和时间放在同等地位,并允许我们从另一个量子系统的角度描述一组量子系统的动态演化,其中其余物理系统演化的参数与作为 QRF 的粒子的固有时间相一致。至关重要的是,两个不同 QRF 中的固有时间与标准变换无关,但它们可能相对于另一个处于量子叠加态。具体来说,我们考虑一个弱引力场中的 N 个相对论量子粒子系统,并引入一个永恒公式,其中 N 个粒子的全局状态似乎“冻结”,但动态演化以关系量的形式恢复。粒子的位置和动量希尔伯特空间用于通过变换到粒子的局部框架来固定 QRF,使得度量在 QRF 的原点处是局部惯性的。内部希尔伯特空间对应于时钟空间,它在粒子的局部框架中保持适当的时间。得益于这种完全关系的构造,我们展示了从 QRF 的角度看,剩余粒子如何在关系变量中动态演化。这里提出的构造包括当忽略外部自由度时非相互作用时钟的 Page-Wootters 机制。最后,我们发现可以在 QRF 中观察到引力红移的量子叠加和特殊相对论时间膨胀的量子叠加。
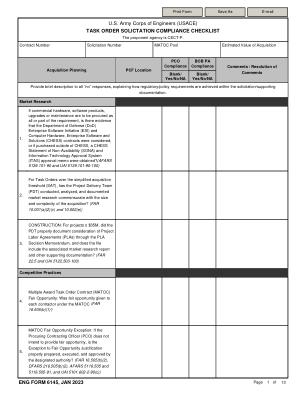
任务订单征集合规检查表
如果考虑成本加奖励费用 (CPAF) 合同/任务订单,包括同时包含固定价格和 CPAF 要素的合同(“混合”),是否已准备 FAR 16.401(d) 所要求的裁定和认定 (D&F)、审查其法律充分性并在相应级别获得批准?(UAI 5101.602-2-90、5106.302-4 和 5116.4)注意:对于与军事建设或军人家庭住房项目相关的合同,根据 DFARS 216.301-3,合同官员不得使用成本加固定费用、成本加奖励费用或成本加激励费用合同类型。
二维缺陷半导体 In 中的本征空位
摘要 开发一种先进的人工智能光电信息系统,精确模拟光子痛觉感受器,类似人类视觉痛觉通路的激活过程,至关重要。可见光到达视网膜,供人类视觉感知,但过度照射会对附近组织造成损伤,但可见光引发痛觉感受器的报道相对较少。本文引入一种二维天然缺陷III-VI族半导体β-In 2 S 3,利用其宽光谱响应,包括本征缺陷带来的可见光,用于可见光触发的人工光子痛觉感受器。该装置在可见光激发下的响应模式与人眼非常相似。它完美地再现了人类视觉系统的痛觉特征,例如“阈值”、“放松”、“不适应”和“敏感化”。其工作原理归因于与In 2 S 3 纳米片中本征空位相关的电荷捕获机制。这项工作为宽带人工光子伤害感受器提供了一种有吸引力的材料系统(本征缺陷半导体)。
立方碳化硅3C-SiC本征缺陷的理论研究
图 2. 示意图,说明评估长程屏蔽能量对带电缺陷的 DFT 超胞计算的贡献。 (a) 带电荷 q 的体缺陷具有无限延伸的电介质屏蔽,内接正方形表示计算超胞的范围。 (b) DFT 超胞将整个净电荷 q 限制在超胞平行六面体内,通过从超胞边缘抽取电子来屏蔽近缺陷区域,从而对边缘区域进行去屏蔽。 (c) 等效体积球体,半径为 R vol ,需要围绕该球体评估长程屏蔽能量。 (d) 该半径减少了 R skin 以解释未屏蔽的晶胞体积,从而得到了由 R Jost 定义的 Jost 经典电介质屏蔽。
请求非征信服务的报价...
…………………………………………………………………………………… …………………………………………………………………………………… Anticipated Contract Duration: ………………………………………………….将完成工作的位置,将提供好/服务:………………………………………………………………………………………………………………………………………………………………………………承诺I………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………[插入公司的全名]特此以书面形式承担,我的公司将在所有相关时间完全符合《劳动法》的相关规定以及适用的集体协议的条款和条件。我完全意识到,如果不遵守此项,则应导致2007年《工党法》第138条规定的诉讼,其中包括但不限于取消合同/许可/授予/许可/许可证或特许权。签名:………………………………..日期:……………………………………………………………………………………………………………………………………………………