XiaoMi-AI文件搜索系统
World File Search System4.3.1-机构-频繁更新-...
3.3. 限制。客户不得让第三方或除客户员工、学生、员工讲师和员工研究人员(其职责要求访问或使用)以外的任何人访问或使用许可材料。在使用之前,客户应确保所有此类学生、员工讲师和员工研究人员均已获悉本条款中有关许可材料的条件、限制和限制,并且客户应对此类用户的行为或疏忽向 Cadence 负责,如同它们是客户的行为或疏忽一样。客户不得对软件或设计元素或任何软件或设计元素的输出进行任何基准测试(这意味着对许可材料与竞争工具产品进行任何形式的竞争分析),也不允许任何第三方这样做。客户应确保通过使用许可材料生成或验证的任何设计和输出均不被客户或任何第三方许可、出售、转让或以其他方式进行商业利用,也不被披露或转让给任何第三方(本第 3.3 条明确允许的除外),也不被用于“使用”定义未明确允许的任何其他目的。”尽管有上述规定,客户可以在以下情况下披露通过使用许可材料生成或验证的设计和输出:
都灵理工学院机构库
过去几年中,量子信息论的最新发展强烈推动了复杂量子现象的表征。在这样的框架中,一个关键概念就是纠缠。纠缠除了被认为是量子计算和通信任务的基本资源 [1] 之外,还被用来更好地表征不同多体量子系统在相关哈密顿量的某些特征参数发生变化时的临界行为;后一种现象被称为量子相变 (QPT) [2]。事实上,人们还没有完全深入理解 QPT 的普遍性质。在这种情况下使用纠缠的特殊之处在于,作为量子关联的单一直接测度,它应该允许对 QPT 进行统一处理;至少,每当发生的 QPT 归因于系统的量子性质时,这总是在 T 0 时,因为不存在热涨落。 [3] 中首次描述了自旋 1=2 链中单自旋或双自旋纠缠与 QPT 之间的关系,其中注意到并发度的导数在 QPT 的对应性上表现出发散,并具有适当的标度指数。随后在 [4] 中研究了 L 自旋块的纠缠及其在表现出临界行为的自旋模型中的标度行为。最近在 [5] 中解决了通过纠缠来表征费米子系统基态相图的问题,其中展示了如何通过研究单点纠缠来重现已知(数值)相图的相关特征。虽然这是一个有希望的起点,但仍需澄清哪些量子关联导致了 QPT 的发生:是两点还是共享点(多部分),是短程还是长程。事实上,要回答上述问题,需要对任何两个子系统之间的纠缠进行详尽的研究。如果子系统只有 2 个自由度,则共生性可以正确量化量子关联 [6]。一个概括
利哈伊保护机构知识库
摘要:近年来,多元同步指数(MSI)算法作为一种新的频率检测方法,在基于稳态视觉诱发电位(SSVEP)的脑机接口(BCI)研究中受到越来越多的关注。然而,MSI算法难以充分利用脑电图(EEG)中与SSVEP相关的谐波分量,限制了MSI算法在BCI系统中的应用。在本文中,我们提出了一种新的滤波器组驱动的MSI算法(FBMSI)来克服该限制并进一步提高SSVEP识别的准确性。我们通过开发一个6命令SSVEP-NAO机器人系统并进行大量实验分析来评估FBMSI方法的有效性。首先使用从9名受试者采集的EEG进行离线实验研究,以研究不同参数对模型性能的影响。离线结果表明,所提出的方法取得了稳定的改进效果。我们进一步对六名受试者进行了在线实验,以评估所开发的 FBMSI 算法在实时 BCI 应用中的效果。在线实验结果表明,FBMSI 算法使用仅一秒的数据长度即可获得 83.56% 的平均准确率,比标准 MSI 算法高出 12.26%。这些广泛的实验结果证实了 FBMSI 算法在 SSVEP 识别中的有效性,并展示了其在改进的 BCI 系统开发中的潜在应用。
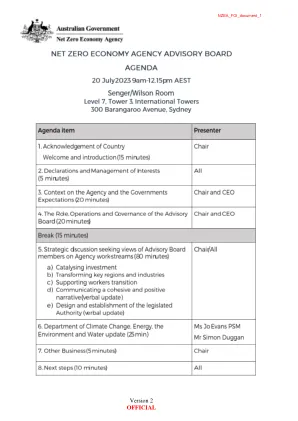
净零经济机构主席和顾问委员会
8/6/23 力拓在澳大利亚拥有大量采矿、材料加工和其他业务,包括皮尔巴拉的铁矿石资产组合,包括采矿业务、铁路网络和港口业务;远北昆士兰的铝土矿、加工设施、港口设施和发电站;以及昆士兰中部的氧化铝精炼厂和塔斯马尼亚和昆士兰中部的铝冶炼厂。因此,力拓可能会受到政府气候变化和脱碳政策的重大影响。为管理任何此类冲突:(a)我不会向力拓披露任何有关政府政策或计划的非公开信息,这些信息是我作为净零经济机构咨询委员会(董事会)成员所了解的。(b)在适当和可行的情况下,董事会应寻求其他主要澳大利亚能源用户和其他可能受到政府气候变化和脱碳政策重大影响的实体(力拓除外)的咨询和意见。(c)我请求并提议,在可行的范围内,
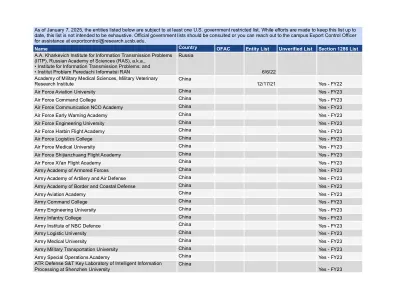
受限制的外国研究机构
名称 国家 OFAC 实体列表 未经验证的列表 第 1286 条列表 中国工程物理研究院 (CAEP) 又名 • 第九院 • 西南计算中心 • 西南应用电子研究所 • 西南化工材料研究所 • 西南电子工程研究所 • 西南环境测试研究所 • 西南火炸药化工研究所 • 西南流体物理研究所 • 西南总体设计与装配研究所 • 西南机械加工技术研究所 • 西南材料研究所 • 西南核物理与化学研究所(又名中国工程物理研究院 (CAEP) 902 研究所) • 西南特种材料研究应用研究所工厂 • 西南结构力学研究所 • 上海高功率激光实验室 • 北京应用物理与计算数学研究所 • 901 研究所
都灵理工学院机构库
蒙特卡洛 (MC) 方法已用于计算半导体中的半经典电荷传输超过 25 年,是微电子器件模拟最强大的数值工具 [1]。然而,当今的技术将器件尺寸推向了极限,传统的半经典传输理论已不再适用,需要更严格的量子传输理论 [2]。为此,人们提出了各种基于格林函数 [3] 或维格纳函数 [4] 方法的电荷传输量子动力学公式。虽然这种量子力学形式允许严格处理相位相干性,但它们通常通过纯现象学模型描述能量弛豫和失相过程。人们还提出了一种用于分析载流子-声子相互作用下的瞬态传输现象的完整量子力学模拟方案 [5]。然而,由于需要大量计算,其适用性仍然仅限于短时间尺度和极其简单的情况。因此,尽管人们付出了很多努力,尽管在研究这些量子动力学公式方面取得了无可置疑的智力进步,但它们在强散射动力学存在下的实际设备中的应用仍然是一个悬而未决的问题。Datta、Lake 和同事的最新成果似乎很有希望 [6]。然而,他们的稳态格林函数公式不能应用于时间相关的非平衡现象的分析,而这种现象在现代光电器件中起着至关重要的作用。在本文中,我们提出了一种广义 MC 方法来分析量子器件中的热载流子传输和弛豫现象。该方法基于控制单粒子密度矩阵时间演化的动力学方程组的 MC 解;它可以被视为对开放系统的扩展
都灵理工学院机构库
摘要:货运业预计将保持甚至增强其在主要现代经济体中的基础性作用,因此,采取行动限制日益增长的环境压力迫在眉睫。使用电力是实现运输脱碳的主要选择;在重型车辆领域,它可以以不同的方式实现:除了全电池动力系统外,电力还可用于供电给接触网道路,或可以化学方式储存在液体或气体燃料(电子燃料)中。虽然目前的欧盟立法采用了从油箱到车轮的尾气排放方法,可实现所有直接使用电力的零排放,但从油井到车轮 (WTW) 方法可以考虑使用可持续燃料(如电子燃料)的潜在好处。在本文中,我们对使用电力为重型车辆供电的选项进行了基于 WTW 的比较和建模:电子燃料、电子液化天然气、电子柴油和液态氢。结果表明,直接使用电力可以节省大量温室气体 (GHG),而使用低碳强度电力生产电子燃料也可以节省大量温室气体。虽然大多数研究只关注绝对的温室气体减排潜力,但考虑新基础设施的必要性以及某些方案的技术成熟度对于比较不同的技术至关重要。本文对此类技术和非技术障碍进行了评估,以比较重型行业的替代途径。在可用的选项中,使用直接使用、能量密集型液体燃料的灵活性代表了脱碳的明显且巨大的直接优势。此外,本文采用的新方法使我们能够量化使用电子燃料作为化学储存的潜在好处,这种化学储存能够从可变可再生能源的生产峰值中积累电能,否则这些电能会因电网限制而被浪费。
金融机构的管理(F000722)
•BASEL III,TLAC,SREP,BRRD,压力测试•定量影响分析4资产负债管理(ALM)•资金来源和资金成本•用于管理利率风险的定量方法管理持续时间风险•价值分析•风险的价值,风险模型•(不便的)贷款范围和贷款范围•贷款范围•贷款范围•贷款范围portforio•贷款范围•贷款范围•贷款范围•贷款范围•贷款范围•贷款范围。在过渡中的银行业务模型•金融科技开发的影响学生还必须准备和捍卫大约5名学生团队中的案例。小组分配的重点是使用基于会计的信息以及市场数据(股票市场收益)的欧洲银行的绩效和风险分析。小组工作的目的是应用适当的定量技术来调查以不同商业模式为特征的欧洲银行的回报/风险权衡。分析的结果得到了介绍和辩护。仅适用于MBF学生:较短,更集中的作业允许学生在例如中应用定量技术。利率风险管理和资本充足性分析。