XiaoMi-AI文件搜索系统
World File Search System量子条件概率
此外,我们证明,当不存在合法的密度矩阵 ρ y 时,联合统计量 p ( x, y ) 是非经典的。这是因为一旦我们消除 p ( x, y ) 中的量子噪声,所获得的无噪声联合分布 P ( x, y ) 就会取负值。非经典是指无法用经典理论解释的属性。确切地说,揭示非经典特性的最有力和最标准的方式是通过缺乏互补可观测量的真正联合分布,就像量子光学中的 Glauber-Sudarshan P 分布的情况一样 [4]。通常,这以观察过程的形式出现,在经典物理学中会导致合法的联合概率分布,但在量子物理学中却无法提供它。这是我们将在本文中遵循的形式主义思想,已在参考文献 [14、15、16、17、18、19、20] 中提出并进行了广泛讨论。值得注意的是,我们的工作不是关于精确联合概率 P ( x, y ) 的定义或构造,而是关于通过实际方法获得噪声联合分布 p ( x, y ) 后的条件概率。精确联合分布 P ( x, y ) 只是作为非经典行为的证据。
量子条件概率和量子信息的新度量
量子信息主要从von Neumann熵和相关数量[1,2]来理解。由于典型的量子现象,例如纠缠等量子,量子信息度量(例如有条件的von Neumann熵和互助的von Neumann信息),即填充了良好的潜在概率分布。尽管如此,尽管它们有些神秘的概念上的基础,但这些数量已被证明可用于重新构架和阐明量子信息的各个方面。经典信息度量所满足的许多关系都反映出它们的量子类似物[1-3],有时非常明显,就像在强大的亚添加性的情况下一样[4]。在本文中,我们定义并研究了补充标准量的新形式的量子信息。我们方法中的关键成分是[5,6]中首先研究的有条件概率分布,该分布为所描述的信息类型提供了基础图片。特别是,我们能够在开放量子系统的上下文中提供信息流的描述,这些量子系统的动力学进化被线性,完全积极的,痕迹的(CPTP)映射良好,而没有任何明确吸引更大的Hilbert Space或辅助系统。我们表明,量子信息理论的某些标准结果从我们的角度自然而然地出现。第2节提供了一些有关经典和量子信息的相关背景。在第3节中,我们从量子条件概率方面定义了新的量子条件熵和量子相互信息的新形式,并且布里层描述了对这些数量的动态解释。在第4节中,我们使用上一节的结果来分析熵增长(在香农的意义上)的过程,并提供了von Neumann熵和量子数据处理的新证明。我们证明我们的量子数据处理不平等提供了自然的解释
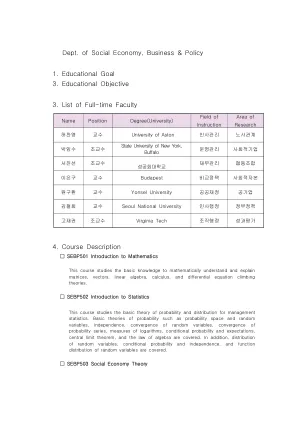
社会经济、商业与政策系
统计学。涵盖概率空间和随机变量、独立性、随机变量的收敛性、概率级数的收敛性、对数测度、条件概率和期望、中心极限定理和代数定律等概率的高级理论。此外,还涵盖随机变量的分布、条件概率和独立性以及随机变量的函数分布。
PHYS 4P51:量子力学 2022 年秋季讲义
3.2.2 对偶向量、内积、范数和希尔伯特空间 ..................................................................................23 3.2.3 正交基 ..................................................................................................................................25 3.2.4 矩阵和伴随矩阵 ..................................................................................................................27 3.2.5 外积 ..................................................................................................................................27 3.2.5 外积 ..................................................................................................................................27 29 3.2.6 完备性关系 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 3.2.10 矩阵内的内积. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ... 42 3.2.17 柯西-施瓦茨不等式..................................................................................................................................................44 3.3 概率论..................................................................................................................................................................................45 3.3.1 随机变量和概率分布..................................................................................................................................................45 3.3.2 条件概率..................................................................................................................................................................................45 3.3.2 条件概率..................................................................................................................................................................................45 . ...
扩散模型的行为克隆
模仿学习通过观察专家的演示而无需访问环境奖励信号来解决学习的挑战。大多数现有的模仿学习方法不需要与环境进行交互,要么将专家分布建模为条件概率p(a | s)(e。g。,行为克隆,BC)或关节概率P(s,a)。尽管简单地用BC对条件概率进行建模,但它通常在概括方面挣扎。在建模关节概率可以提高概括性能时,推理过程通常是耗时的,并且模型可能会遭受过度拟合的歧视。这项工作提出了一个模仿学习框架,该框架从建模专家分布的条件和联合概率中受益。我们提出的扩散模型启动行为克隆(DBC)采用了一种扩散模型,该模型训练了建模专家行为,并学习了一项政策,以优化BC丢失(条件)和我们提出的扩散模型损失(关节)。DBC在导航,机器人臂操纵,灵活的操纵和运动中的各种连续控制任务中的表现优于基准。我们设计了其他实验,以验证对条件概率或专家分布的关节概率建模的局限性,并比较不同的生成模型。消融研究证明了我们的设计选择的有效性。
机器学习的数学基础-Robert Nowak
1个机器学习的概率1 1.1执行摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1 1.2简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1 1.3关节,边缘和条件概率。。。。。。。。。。。。。。。。。。。。。。。。。。。。3 1.4直方图分类器。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3 1.4.1基本概率计算。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3 1.5期望。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4 1.6独立的渲染变量总和。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 1.7 excergies。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6
量子信息理论解决方案 6
a) 现在我们来看看使用这个量子信道发送经典信息时会发生什么。我们从任意输入概率分布 PX (0) = q, PX (1) = 1 − q 开始。我们将这个分布编码为状态 ρ X = q | 0 ⟩⟨ 0 | +(1 − q ) | 1 ⟩⟨ 1 | 。现在我们通过量子信道发送 ρ X ,即让它在 E p 下演化。最后,我们在计算基础上测量输出状态 ρ Y = E p ( ρ X )。计算条件概率 PY | X = x ( y )
非共同信息几何
1量子概率1 1.1简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1 1.2量子期望。。。。。。。。。。。。。。。。。。。。。。。。2 1.2.1 N-N矩阵的代数。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 2 1.2.2期望值。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 3 1.2.3密度矩阵。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 1.2.1 N-N矩阵的代数。。。。。。。。。。。。。。。2 1.2.2期望值。。。。。。。。。。。。。。。。。。。。。3 1.2.3密度矩阵。。。。。。。。。。。。。。。。。。。。。。4 1.2.4经典概率。。。。。。。。。。。。。。。。。。。。5 1.2.5笔记。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 1.3条件概率。。。。。。。。。。。。。。。。。。。。。。6 1.3.1经验数据。。。。。。。。。。。。。。。。。。。。。。。6 1.3.2更新。。。。。。。。。。。。。。。。。。。。。。。。。。7 1.3.3破坏统计独立性。。。。。。。。。。。。7 1.4历史实验。。。。。。。。。。。。。。。。。。。。。。。8 1.4.1 EPR悖论。。。。。。。。。。。。。。。。。。。。。。8 1.4.2钟的不平等。。。。。。。。。。。。。。。。。。。。10
CSE 473:人工智能
§ 分布 P ( X ) 给出每个可能值 x 的概率 § 联合分布 P ( X,Y ) 给出每个组合 x,y 的总概率 § 求和/边缘化:P ( X=x ) = å y P ( X=x,Y=y ) § 条件概率:P ( X | Y ) = P ( X,Y )/ P ( Y ) § 乘积规则:P ( X | Y ) P ( Y ) = P ( X,Y ) = P ( Y | X ) P ( X )