XiaoMi-AI文件搜索系统
World File Search System监管环境下的人工智能:评估上市公司年度报告
深度学习模型参考多组带标签的训练数据,通过分析嵌入的语义信息来计算内容块与特定上市规则的相关性。带标签的数据被视为正例,其余内容块被视为负例。针对带标签的示例训练分类模型,输出条件概率 P(Y=相关丨内容块),其中不相关的元素块被赋予“0”分数,正确标记的相关块被赋予“1”。所有内容块都有自己的概率,然后按分数排序。
2024-2025 年学习课程
APL101 工程应用中的应用数学 3 学分 (3-0-0) 常微分方程:二阶 ODE、待定系数法、参数变异、Strum-Liouville 特征值问题、差分方程。偏微分方程:PDE 的分类、热、波和拉普拉斯方程、分离变量以解决 PDE。傅里叶变换:傅里叶正弦变换、傅里叶余弦变换、解决 ODE 和 PDE 的技术。概率论:概率公理、条件概率、随机变量、工程系统中的不确定性、离散和连续分布、分布函数、联合概率分布、矩、协方差、相关系数。随机过程:随机过程的定义、随机 FE 模型、平稳过程、马尔可夫链、泊松过程。
电气工程(EENG)
EENG 202a,通信与控制概论 Anna Gilbert 介绍感知、处理、控制和通信的系统。主题包括信息理论和编码(压缩、信道编码);网络系统(网络架构、路由、无线网络);信号和系统(线性系统、傅立叶技术、带限采样);估计和学习(假设检验、回归、分类);以及端到端应用示例(安全、通信系统)。MATLAB 编程作业阐明了概念。学生应该对计数(组合学)、概率和统计(事件之间的独立性、条件概率、随机变量的期望、均匀分布)有基本的了解。先决条件:MATH 115。最好有 AP 统计。QR
基于人类因素 - 量化 - 基于OHFAM-and-...
摘要。发生人为因素分析模型是根据人为因素分析和分类系统(HFAC)以及中国民航的实际操作条件和特征来开发中国民航模型,以增强安全信息的分类,分析和利用。此外,要生成一个可以在航空事件分析中提供定量分析支持的模型,建立了基于OHFAM和贝叶斯网络的人为因素分析模型。通过用CH得分功能梳理爬山搜索方法构建的模型是一个贝叶斯网络,它使用三层节点来表示人为因素和事件之间的因果关系。人为因素对航空事件的特定影响程度由模型的条件概率参数表示。它在航空事件分析和推论中很有用。
在100%可再生能源系统中,第四代地区供暖的好处
摘要:这项研究工作提出了一种新的方法,用于估计使用贝叶斯网络(BNS)的海洋能量转换子系统中能量传输网络可用性状态的概率。可以通过定性系统分析来理解该网络中不同级别的单位之间的逻辑相互关系,然后可以通过故障树(FT)对其进行建模。可以将FT映射到相应的BN,并且可以根据逻辑结构确定节点的条件概率。进行了一个案例研究,以证明如何实施映射,并估算了可用性状态的概率。结果给出了每个可用性状态作为时间的函数的概率,这是选择最佳设计解决方案的基础。
有条件的概率和量子中的后验状态...
本文的目的是提供一个有条件的概率的概念,该概率自然是在连续量子观察物的测量中。量子测量中有条件期望的概念首先出现在中村 - 乌梅格基[11]中,而umegaki [19]在操作者代数理论中已经发展了这种条件期望的形式理论。但是,这种条件期望的概念只能应用于阿尔维森[2]所示的离散可观察物的测量。因此,我们必须从量子测量过程中量子机械条件概率的原始统计解释开始。我们从先验状态确定A后验状态的方法是概率理论中贝叶斯原理的一种变体,该变体首次出现在von Neumann [12; pp。337-346]在量子力学中。
机器学习简介 - 成像科学中心
1通用符号和背景材料15 1.1线性代数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 1.1.1集合和功能。。。。。。。。。。。。。。。。。。。。。。。。。。15 1.1.2矢量。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 1.1.3矩阵。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。16 1.1.4多线性地图。。。。。。。。。。。。。。。。。。。。。。。。。。17 1.2拓扑。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 1.2.1 R. R. 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 17 1.2.2紧凑型集。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。17 1.2.1 R. R.。。。。。。。。。。。。。。。。。。。。17 1.2.2紧凑型集。。。。。。。。。。。。。。。。。。。。。。。。 div>。 div>。 div>。 div>。 div>。 div>18 1.2.3公制空间。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>18 1.3微积分。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>18 1.3.1 d ff Fintials。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>181。1.3.2重要例子。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。。。。。。。。。20 1.3.3高阶衍生物。。。。。。。。。。。。。。。。。。。。。。21 1.3.4泰勒定理。。。。。。。。。。。。。。。。。。。。。。。。。。。21 1.4概率理论。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。23 1.4.1一般假设和符号。。。。。。。。。。。。。。。。23 1.4.2条件概率和期望。。。。。。。。。。。。23 1.4.3测量理论概率。。。。。。。。。。。。。。。。。。。25 1.4.4度量的乘积。。。。。。。。。。。。。。。。。。。。。。。。27 1.4.5相对绝对连续性和密度。。。。。。。。。。。。27 1.4.6测量理论概率。。。。。。。。。。。。。。。。。。。28 1.4.7条件期望(一般情况)。。。。。。。。。。。。。28 1.4.8条件概率(一般情况)。。。。。。。。。。。。。29
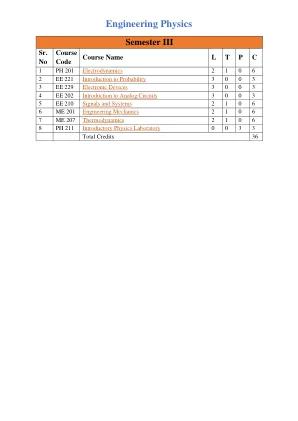
工程物理学
简介:学习本课程的动机、必修基础数学复习、实线子集上概率与长度的关系、概率形式定义、事件与$\sigma$代数、事件独立性与条件概率、事件序列与Borel-Cantell引理。随机变量:随机变量的定义、随机变量的类型、CDF、PDF及其性质、随机向量与独立性、随机变量变换简介、高斯随机向量简介。数学期望:通过例子了解平均值的重要性、期望的定义、矩与条件期望、MGF、PGF与特征函数的使用、方差与k阶矩、MMSE估计。不等式与收敛概念:马尔可夫、切比雪夫、切尔诺夫与Mcdiarmid不等式、概率收敛、均值与几乎必然、大数定律与中心极限定理。随机过程的简要介绍:示例和正式定义、平稳性、自相关和互相关函数、遍历性的定义。
AME 540工程科学的概率和统计
助教:TBD办公室:TBD办公时间:TBD联系信息:TBD IT帮助:DEN Services目录描述概率;随机变量和向量;关节,边缘和条件分布;贝叶斯定理;随机过程简介;统计推断;回归和生成模型。课程描述课程是适用于所有工程学科的概率和统计信息的简介。班级的重点是学习概率和统计数据的基本概念,这些概念在解释工程/科学数据和概率机器学习技术中的应用中找到了应用。该课程的第一部分将重点关注概率空间,随机变量和向量,累积和概率密度函数,关节,边际和条件概率,贝叶斯定理,中央限制定理以及随机过程的简介。在课程的第二部分中,这些想法将应用于包括参数估计,假设测试,回归和机器学习生成模型的统计任务。学习目标的学生成功完成课程