XiaoMi-AI文件搜索系统
World File Search System机器学习驱动的Web-POST屈曲阻力预测高强度钢梁具有基于椭圆形的Web开口
随着全球对气候变化和环境可持续性升级的关注,裁定行业正在大大转移到生态耐性和可持续性的建筑实践上。本文全面探讨了将建筑信息建模(BIM)与环保原则相结合,以创建设计和建造可持续建筑的框架。这项研究引入了一种实用方法,用于评估建筑建筑的体现碳,从缅甸仰光市的一栋住宅建筑中获得见解。本研究开发的方法旨在评估与施工过程不同阶段相关的碳足迹,包括原材料生产和材料运输。补充说,提出的方法比较了两种传统和低碳材料,比较了住宅建筑中材料体现的碳,运输体现的碳和总成本。结果表明,材料体现的碳仅贡献84%,而材料运输占两种情况的剩余16%。利用低碳材料可显着减少,与常规伴侣rial相比,材料体现碳的碳足迹降低了40%,运输碳足迹下降了39%。但是,采用低碳材料会使总成本的适度增加约为6.7%。这项研究强调了将低碳材料整合到未来被动建筑物的设计中的必要性,从而推进了追求零零策略的追求。这项研究强调了BIM驱动的生态弹性实践的潜力,以减轻碳排放,以及在可持续建筑设计和建筑中持续创新和协作的需求。
使用QR码修改和椭圆曲线密码
抽象的身份证或Kartu Tanda Penduduk(KTP)对于印尼人民至关重要。KTP包含个人信息,例如国家身份编号(NIK),姓名,地址,性别等。由于KTP具有必不可少的数据,并且仍在常规上打印,因此如果丢失了KTP,则存在一个漏洞,并且所有者的数据被披露,以便如果不负责任的人找到它,则可以使用数据来模仿所有者。在Haque等人,[1]提出的先前方法中,数据存储在QR码中。但是,没有验证方法可以使原始所有者合法化,并且系统没有登录功能。为了克服Haque等人的弱点,方法[1],使用椭圆曲线EL-Gamal(ECEG)对所有者的NIK进行了加密,并在将其存储在QR码中之前,在将其存储之前使用ECDSA进一步签名。对于在数据库中获取所有者的数据,应在扫描QR码后进行验证过程。使用提出的方法,猜测攻击成功的可能性为1 /(n -1)。同时,模拟攻击成功的可能性为1 /(Q1 * Q2 * L)。
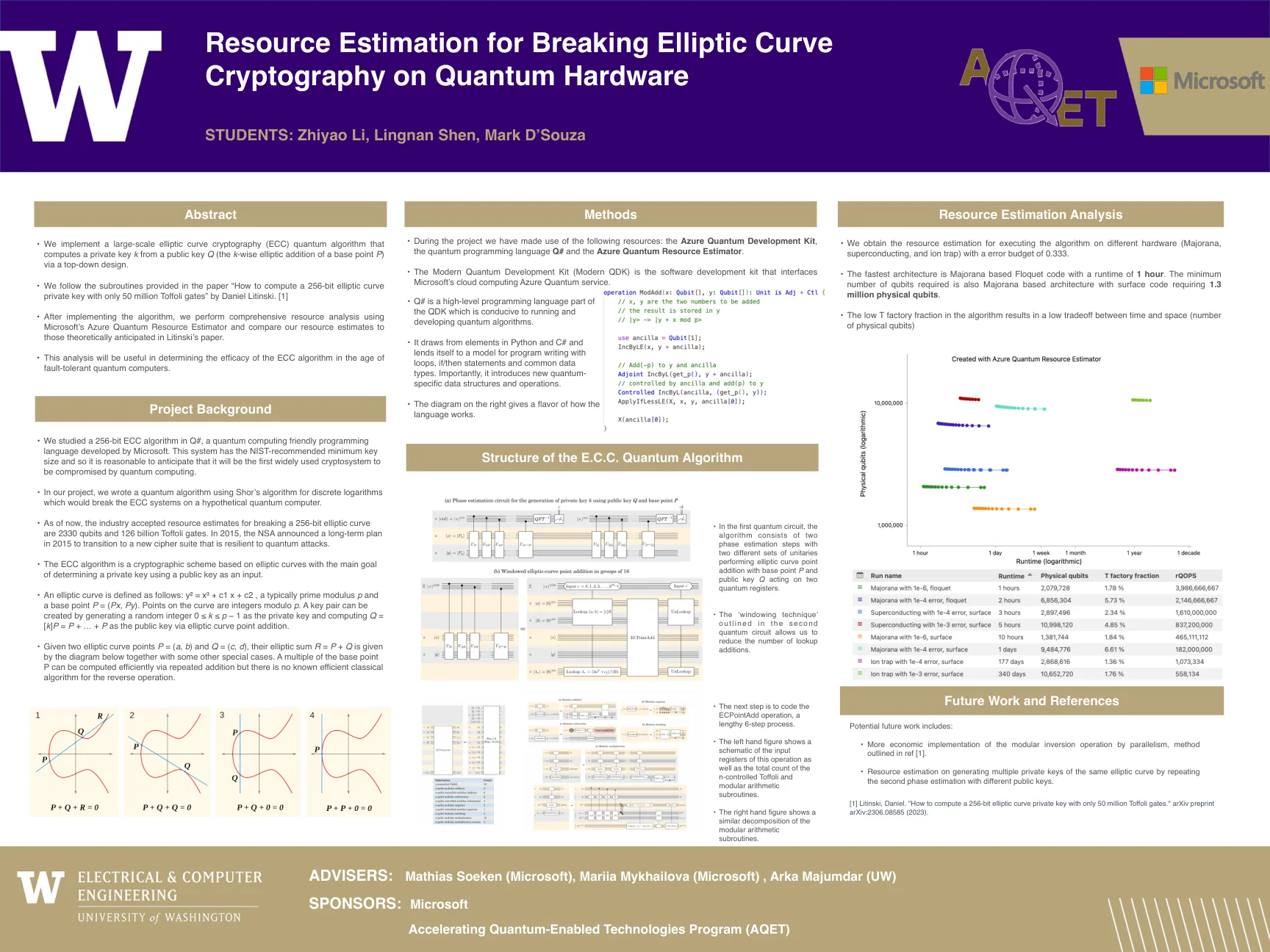
量子硬件上破坏椭圆曲线加密的资源估计
基点P =(PX,PY)。曲线上的点是整数模块。可以通过生成一个随机整数0≤k≤p -1作为私钥和计算q = [k] p = p = p +… + p作为公共密钥通过椭圆曲线点添加作为公共密钥来创建一个键对。
比特币区块链中使用的SECP256K1椭圆曲线的安全性:
摘要:本文深入研究了用于比特币区块链中地址生成的SECP256K1椭圆曲线的复杂特征和安全属性。比特币区块链是一个分散的数字分类帐,记录了用比特币加密货币进行的所有交易。在这项工作中,描述了SECP256K1椭圆曲线及其参数以及使用随机数生成私钥和公共密钥的方法。虽然专用密钥允许签署交易来花费比特币,但相应的公钥和地址使其他人能够验证交易并将资金发送到区块链上的特定地址,以确保分散网络中的安全性,真实性和隐私性。讨论了对使用SECP256K1的使用来生成诸如蛮力攻击,扭曲攻击,故障攻击以及椭圆曲线实施中的侧渠道攻击之类的比特币地址。通过维护SECP256K1的安全性和完整性,我们可以确保加密操作(例如数字签名和关键交换)仍然不妥协。如果曲线的安全性受到了损害,恶意用户可能会从公共钥匙中衍生出私钥,从而导致未经授权的交易,双人支出或其他恶意活动。可以通过确保使用SECP256K1进行彻底的测试和验证以确保正确且安全的操作来增强实施的安全性。讨论了对区块链技术的重要攻击,例如51%的攻击,SYBIL攻击,双重支出攻击和智能合同漏洞。通过全面的探索,读者将了解为什么选择这种特定的椭圆曲线以用于比特币的加密协议中,从而强调了其在确保区块链生态系统的鲁棒性和完整性方面的作用。
蓝色椭圆形SK电池公园环境影响和社区指南
我代表我的顶峰和抽象是我的原始作品。适当地归因于所有外部来源。我知道我完全负责获得任何必要的版权权限。我已经从每个第三方受版权保护的事项的所有者那里获得了所需的书面许可声明,该事项将包括在我的工作中,允许电子发行(如果公平使用学说不允许使用这种使用),将其作为附加文件提交给UKnowledge。
1线粒体总是显示为椭圆形
线粒体形态的研究更多地是在培养的细胞而不是天然细胞中进行的。The issue with this disparity has been highlighted by a study of vascular smooth muscle cells, of which those that were cultured cells appeared to offer more mitochondrial morphological diversity than in those that are native, which rather have singular spherical or rod-like mitochondria (with native cells in most tissues being found to have these similar, punctuate mitochondria), making it unlikely that observing ovoid shapes is due to氧化应激或成像难度。进一步的证据表明,遵守线粒体形状的传统观念包括未发现天然细胞的线粒体是电耦合的 - 它们的膜电位变化是独立的,而不是作为公共变化的一部分,这将在形成连续网络的细胞器中观察到。图1介绍了这项研究中线粒体和培养细胞中线粒体的图像。
超级椭圆曲线基于同一基于量子的量子加密密钥交换方案
1汤姆(J. J.),*,2 Onyekwelu,B。A.,3 Anebo,N。P. 4 Nwanze,A。C. 5 Akpan,A。G. 6 Ejodamen,P。U.1,2尼日利亚伊利亚州伊利诺拉大学计算机科学和网络安全系3尼日利亚奥托克大学计算机科学系3,尼日利亚丹尼斯·奥萨德贝大学4号计算机科学系,尼日利亚阿萨巴,计算机科学学院,计算机科学学院5尼日利亚伊布萨。通讯作者的电子邮件地址:1 joshua.tom@elizadeuniversity.edu.ng, +234-0803-078-1045,2 bukola.onyekwelu@elizadeuniversity.edu.edu.edu.ng,3 nlerumpa@fuotuote@fuotuoke.eduoke.edu.ng,4nwang.ng.ng.ng.ashe.ashe.ashe.ashe.ashe.ashe.ashe.ashe.ashe.ashe.ashe.ashibashe,,, abasakpan@futia.edu.ng,6 piusejodamen@adun.edu.ng
在密码学中使用椭圆曲线的方法
在1984年,Schoof提出了一种用于计算椭圆曲线顺序的多项式时间算法。尽管有了理论的进步,但该算法的实际性能很差,从而限制了其在加密环境中的应用。随后,Elki引入了Elki Prime数字和Atkins Prime数字,在最终字段中提供了更广泛的背景。它们的算法显着提高了计算椭圆曲线顺序的效率。同样,Lesieu提出了一种基于形状效应的计算方法,得出了可比的结果。后来,Sato和Harley开发了一种更有效的算法,以及一种简单而有效的计算方法,从而得到了显着改进。