XiaoMi-AI文件搜索系统
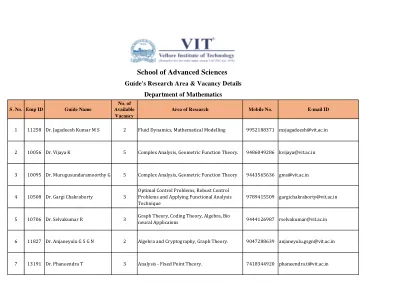
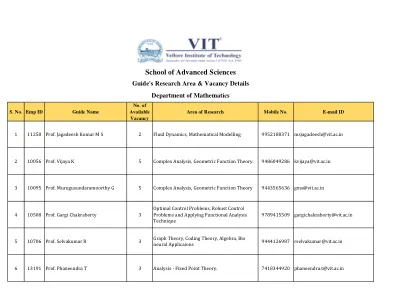
World File Search System数学指南研究-AREA-and-VACANCH- ...
29 14075 Venkateswarlu教授b 4代数,图理论,使用操作研究的模糊集,优化技术9994462955 venkatesh.reddy@vit.ac.ac.in
一种排名间隔估值的梯形直觉的方法...
一个任务问题在行业,决策分析以及工程和管理科学中的许多其他应用中起着至关重要的作用。间隔有价值的梯形直觉模糊集(IVTRIFS)是捕获不确定性的强大工具。当应用模糊集理论用于研究任何现实生活问题时,Ivtrifss的排名是必不可少的。在本文中,通过使用犹豫不决的重心(COG)的概念来介绍一种对IVTRIFSS进行排名的新方法,该概念易于计算,易于使用以比较Ivtrifss。使用数值示例将提出的方法与现有方法进行比较。此外,使用所提出的方法讨论了IVTRIFSS环境下的分配问题。关键字:分配问题,模糊数字的排名,间隔有价值的直觉梯形
使用多参数进行高机动目标跟踪...
目前,已提出了许多大机动目标跟踪算法[1~14],其中Singer模型[15~18]是常见的机动目标跟踪模型,适用于多种情况和各种类型的机动,但强机动会引起较大的跟踪误差,由于目标机动性的不确定性和模糊性较强,特定的模型参数很难适应目标的强机动变化。模糊推理方法[19,20]属于基于模糊集理论和模糊数学的模糊控制方法。自从1965年Zadeh提出模糊集的概念以来,模糊系统的研究得到了迅速发展,模糊控制技术在工业生产控制中得到了广泛的应用。为了适应复杂多变的运动模式,提高Singer模型在强机动跟踪情况下的性能,在
在量子退火器上实现去模糊化算子
摘要 — 由于量子计算的内置并行性,未来量子计算机在处理一些复杂的模糊逻辑计算方面具有未被开发的潜力。最近,在一种称为量子退火器的量子计算机上,引入了一种基于解决二次无约束二进制优化 (QUBO) 问题的模糊集的新表示和一些基本模糊逻辑运算符 (并集、交集、alpha 切割和最大值) 的实现。本文通过提出一种基于二进制二次模型 (BQM) 的量子退火机上的质心去模糊化的实现来扩展这项工作,但这次使用的是 Ising 模型。通过在量子计算机上实现基本操作和去模糊化,本文为在量子退火器等增强型设备上实现整个模糊推理引擎铺平了道路。索引术语 — 量子计算、模糊逻辑、模糊集。
间隔有价值的次级K范围对称Quadri分区的中性粒细胞模糊矩阵
间隔价值的二级K范围对称Quadri分区的中性粒细胞模糊矩阵是一个高级数学框架,它扩展了传统的矩阵理论,以处理复杂系统中的不确定性,不确定性和不一致性。该模型从中性粒子逻辑,间隔值模糊集和矩阵理论中整合了多个数学概念,以提供一种多功能工具,用于在不确定的环境中表示和处理数据。中性粒子逻辑是模糊逻辑的扩展,它引入了三个成员资格功能 - truth(t),虚假(f)和不确定性(i)。与传统的模糊逻辑不同,中性粒子逻辑可以同时在给定的命题或元素中在不同程度上同时存在真理,虚假和不确定性。中性粒细胞模糊基质代表一个基质,其元素是中性粒细胞模糊集。矩阵中的每个元素的特征是有序的三重(t,i,f),其中:
模糊逻辑在人工智能中的位置
到目前为止,“模糊逻辑”一词通常指一种特定的控制工程方法,该方法利用常识控制规则的数值表示,以便通过插值合成控制律。这种方法与神经网络有许多共同特征。它现在主要关注数值函数的有效编码和近似,目前与知识表示问题的关系越来越少。然而,这是对模糊逻辑的非常狭隘的看法,与人工智能关系不大。扫描模糊集文献,人们意识到模糊逻辑也可能指另外两个与 M 相关的主题:多值逻辑和近似推理。虽然多值逻辑流非常以数学为导向,但 Zadeh 设想的近似推理概念与人工智能研究的主流程序更相关:他在 1979 年写道:“近似推理理论涉及从一组不精确的前提中推导出可能不精确的结论”。在下文中,我们将使用术语“模糊逻辑”来指代任何一种旨在用于推理机制的基于模糊集的方法。
犹豫模糊隶属函数估计下生物质供应链网络设计的可能性规划方法
摘要:通过从专家那里获取知识来识别隶属函数是许多模糊数学规划模型的重要因素。同时,犹豫模糊集理论作为一种已知且流行的现代模糊集,通过在集合下分配一些离散隶属度,可以适当地处理决策问题中的不精确信息。因此,犹豫模糊隶属函数 (HFMF) 估计可以帮助数学规划方法的用户在连续空间问题中提供强大的解决方案。因此,本研究提出了一种基于贝塞尔曲线机制的可能性规划方法来估计 HFMF。在可能性规划方法的过程中,提出了一个优化模型来调整贝塞尔曲线的主要参数,目标是最小化经验数据和拟合 HFMF 之间的 SSE)。之后,通过提出一种新的生物质供应链网络设计问题数学模型来检查所提方法的效率和适用性。最后,提供了关于生物质供应链网络设计的计算实验和验证程序,以仔细检查所提出方法的验证和确认。
4ee65:人工智能(ai)应用
1 小时。人工智能和模糊系统简介:人工智能:定义、意义、范围和应用。模糊系统:模糊集和运算、成员函数、模糊化和去模糊化、规则库、模糊逻辑控制简介、Mamdani 和 Takagi-Sugeno 模糊模型的架构、电力驱动、工业自动化、可再生能源系统、电动汽车、智能电网等领域的实施。
基于模糊的故障模式、影响和关键性分析应用于网络电网
摘要:故障模式、影响和危害性分析 (FMECA) 是一种定性风险分析方法,广泛应用于各种工业和服务应用。尽管该方法广受欢迎,但多年来,文献中分析了该方法的几个缺点。获取故障模式风险水平的传统方法不考虑风险因素之间的任何相对重要性,并且可能不一定代表 FMECA 团队成员的真实风险感知,通常用自然语言表达。本文介绍了 I 型模糊推理系统 (FIS) 的应用,作为改进经典 FMECA 分析中故障模式风险水平计算的替代方案,以及它在网络电网中的应用。我们基于模糊的 FMECA 首先考虑由 FMECA 专家定义的一组模糊变量,以体现与人类语言相关的不确定性。其次,使用“七加或减二”标准来设置每个变量的模糊集数量,形成一个由 125 条模糊规则组成的规则库,以表示专家的风险感知。在电力系统框架中,新的基于模糊的 FMECA 用于网络电网系统的可靠性分析,评估其相对于传统 FMECA 的优势。本文提供了以下三个关键贡献:(1) 使用模糊集表示与 FMECA 专家相关的不确定性,(2) 通过