XiaoMi-AI文件搜索系统
World File Search System个人简历 MARIA HADJINICOLAOU 个人...
研究兴趣:物理、生物医学和工程问题的多尺度数学建模,例如:红细胞(RBC)或LDL周围的血浆流动、弯曲血管中的血流(无论是否动脉粥样硬化)、药物输送和吸收、肿瘤生长、多孔介质中的斯托克斯流、纳米级(石墨烯)和宏观尺度下固体材料在不同机械载荷下的行为和特性,以及:由简单和许多具有不同物理特性和几何形状的散射体引起的波传播和散射问题(直接和逆)、移动边界问题、开发和使用非侵入性技术进行医学诊断、测试、识别和重建物体和图像。
使用机器学习预测低电离层参数和低频天波传播强度
研究低频无线电波传播预测对于支撑固定和移动长距离通信、遥控导航、授时服务等应用具有重要意义。因此,为提高低频天波传播的预测精度,提出了一种基于机器学习的改进方法。首先,利用机器学习的方法建立对低频天波传播影响显著的低电离层E层临界频率(fo E)的预测模型。其次,基于低电离层参数模型增强了低频天波传播的预测方法。通过对比东亚地区实测数据和基于跳波理论的预测数据,提出的方法使低频天波场强提高了6.16%。
ITU-R BT.1872-3 建议书 – 广播辅助服务的用户要求,包括数字电视室外广播、电子/卫星新闻采集和电子现场制作
BO 卫星传送 BR 录制用于制作、存档和播放;电视影片 BS 广播业务(声音) BT 广播业务(电视) F 固定业务 M 移动、无线电测定、业余和相关卫星业务 P 无线电波传播 RA 射电天文学 RS 遥感系统 S 卫星固定业务 SA 空间应用和气象学 SF 卫星固定业务和固定业务系统之间的频率共享和协调 SM 频谱管理 SNG 卫星新闻采集 TF 时间信号和频率标准发射 V 词汇和相关主题
从双缝到量子比特
量子现象表现出“波粒二象性”——也就是说,量子系统在未被观察到的情况下会以波的形式演化(即,波穿过两个狭缝并随后与自身发生干涉)——但是当按照客观(经典)现实进行测量时,波函数就会崩溃,它确实具有客观现实(即,作为一个光子,或者如果你喜欢的话,它是一个穿过两个狭缝之一的小“球”)。因此,我们对量子系统的数学描述应该足以允许这两种可能性——它既应该能够确定(概率)测量结果,又应该完全捕捉随后的波传播(如果没有进行测量)。特别是,根据假设 1,系统完全由其状态向量描述,因此双缝处的量子态必须完全捕捉有关波粒二象性的一切。对于两级量子系统(量子比特),我们可以定性地认识到,计算基向量的复叠加具有所需的成分。计算基向量(| 0 ⟩ 和 | 1 ⟩)表示测量时可能出现的二元状态(即光子通过了哪条狭缝)——其复系数不仅能够计算出每种状态的概率,而且也足以确定后续的波传播(即屏幕右侧)(如果没有进行测量)(这就是它们必须是复数的原因)。这也提供了一种思考计算基的好方法,即在某种意义上用客观现实来表示“经典”事件,而对其的测量只是通过波函数坍缩来获得和确定这种经典现实。也就是说,量子测量只是用电压表、电流表、信号分析仪或其他仪器进行的常规测量。我们引入一般测量假设是为了完整性,但在第二部分 CST 量子计算课程中,我们几乎总是使用具有这种有形物理解释的计算基础测量。
主题索引 - ASTM International
声波,536-546 衍射和模式转换信号,541-542 分布弹簧常数,539-541 与裂纹的相互作用,536-537 界面透射率,539,541 局部应力强度因子,543-546 通过透射和衍射信号接收,537-538 界面残余应力,542-543 剪切波信号,542 超声波穿过裂纹的传播,539-540 垂直于裂纹表面的波传播,538--541 艾里应力函数,313 合金,139,171 铝合金,121,270,528,583-597,640,642-643 施加与有效试样几何形状,227-228 基线传播数据,571-572 化学成分, 122,584 顺应性方法,587 恒定载荷振幅试验,569-570 裂纹扩展基线数据,428-430 速率变化,37-38 裂纹张开应力强度因子变化,37-38
引用Zainab N. Mutashar和Sura N. Taraad(2025)。各向异性超材料对圆柱波
超材料是人为设计的材料,旨在具有天然材料中未发现的电磁场的性质。各向异性超材料的电磁特性取决于方向,这为它们提供了控制传统材料无法控制波动的能力。这些属性就像在大规模影响波传播的超材料元件之间的复杂相互作用,例如分散,衰减和波浪的极化[6]。各向异性超材料由定向电导率,渗透率和介电量张量定义。与典型的各向同性材料不同,这些参数不是不变的;相反,它们是方向依赖性的,因此导致材料内部的波浪行为复杂。上述特征可以由张量表示,张量概述了多维材料波相互作用[7]。
编辑:使用有限元方法的周期性结构理论的应用
周期性结构包括重复单位细胞。从人造的多跨桥到天然存在的原子网格,到处都有周期性结构。Brillouin(1953)首先使用波传播方法来研究周期性晶格的动力学。周期性配置在半导体和晶体中创建电子带的能力类似于弹性介质的结构/声学带。加固的板和壳结构经常用于多种结构应用中,包括桥梁,船体,甲板,飞机和航空飞机火箭/导弹结构,这些结构是周期性结构的示例。Mead(1996)详细概述了有关周期结构振动分析的可用文献。在均质/异质复合结构,波导,音调晶体(PC),声学/弹性超材料,振动声学隔离,噪声抑制设备,振动控制,有向能量的振动等区域中,这可能会导致出色的实施。周期性结构还用于研究滤波器特征(Zheng等,2019)的可调节性,例如所需的声带隙,传播,截止频率,衰减和响应方向。健康监测(Groth等,2020)和对这些结构的损害检测需要很好地了解通过这种周期结构的弹性波的传播。尤其是对电磁波运动的影响(Pierre,2010年)已被广泛研究,并且已应用于许多光学和电磁设备(Bostrom,1983)。有限元(FE)基于理论的数值方法在对各种数值方法之间进行物理结构进行建模时表现出最多的多样性和有用性。使用FEM(PSFEM)的周期性结构中的波传播理论是研究主题的目标,数值解决方案基于结构单位单元的Fe分析。这种数值FE方法可以通过很少的计算工作来实现高精度,并且推荐的选择是预测一维和二维单一波导中的波动(Orris and Petyt,1974; Pany等,2002; Pany and Parthan and Parthan,2003a,2003a; Pany et and; Pany et al。大多数已发布的
bragg反射器对电磁波的散射...
摘要。我们解决了平面波在由DC横向磁场控制的铁氧体1D磁磁晶体上散射的问题。基于Floquet-Bloch理论的混合边界条件的山山方程溶液以分析形式获得。明确发现色散方程及其根。根据铁氧体层的材料参数,对结构的分散性质进行分析。确定具有有限周期数量的陀螺仪的传输和反射系数。考虑了两个特征情况:旋转层有效渗透性的正值和负值。在晶体时期确定电磁场组件的空间分布的表达。结果提供了对具有控制旋转元素的多层介质中电磁波传播行为的更深入的理解。此外,获得的分析表达式简化了这种复杂介质中波过程的分析。
使用声学和光子学的物理神经网络
4基于任意可编程波传播的光子处理器44 4.1简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。44 4.2设备的操作原理。。。。。。。。。。。。。。。。。。。。。。。。47 4.3机器学习演示,具有2D可编程的波导。。。50 4.4讨论和前景。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。53 4.5方法。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。55 4.6数据可用性。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。65 4.7代码可用性。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。65 4.8致谢。。。。。。。。。。。。。。。。。。。。。。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>65 4,99授权。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>66 div>
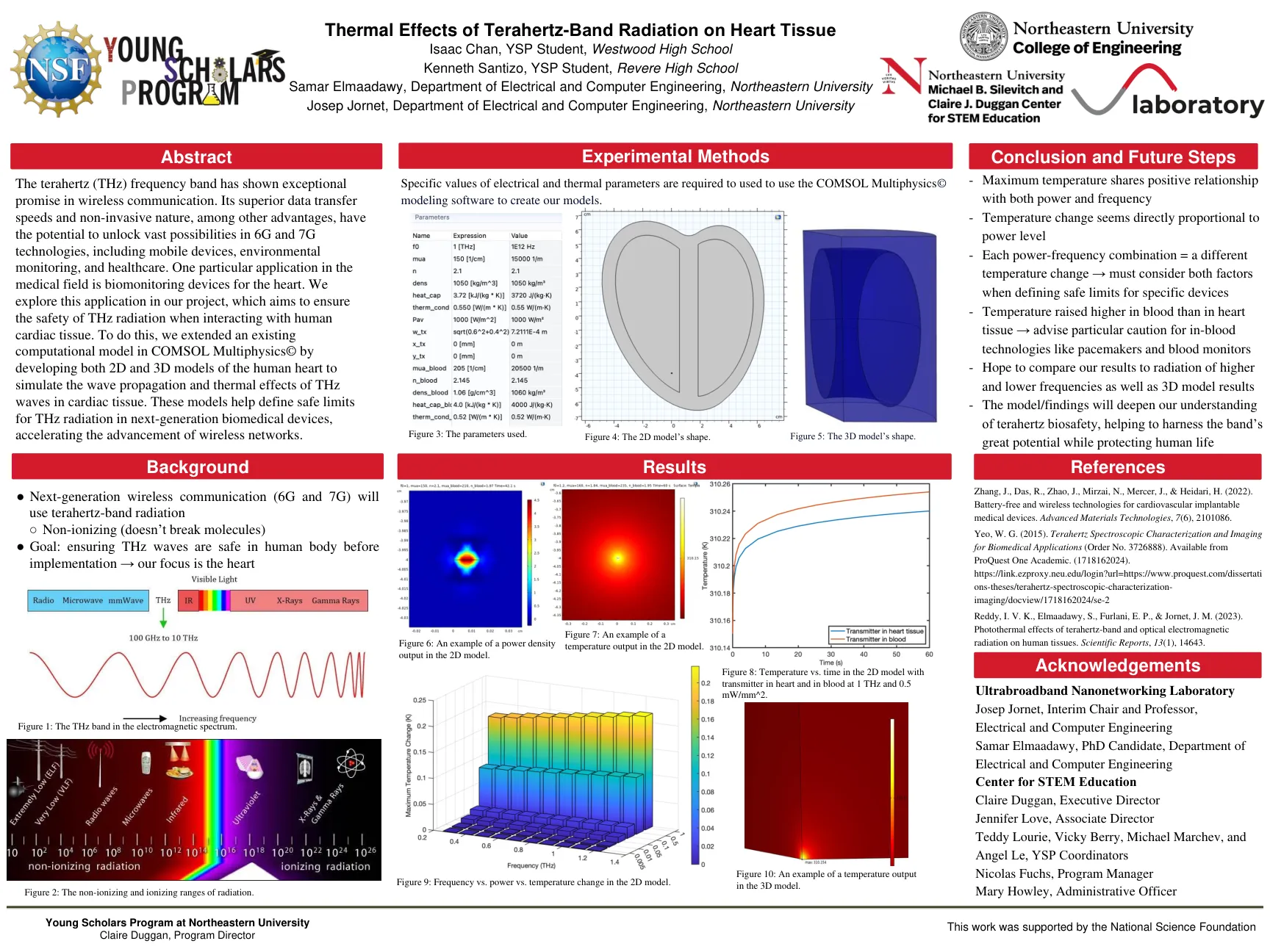
Terahertz波段辐射对心脏组织的热效应
Terahertz(THZ)频带在无线通信中表现出了非凡的承诺。其出色的数据传输速度和非侵入性质,除其他优势外,还具有在6G和7G技术(包括移动设备,环境监测和医疗保健)中解锁巨大可能性的潜力。医学领域中的一个特定应用是心脏的生物监测设备。我们在我们的项目中探讨了这一应用,该应用程序旨在确保与人类心脏组织相互作用时THZ辐射的安全性。为此,我们通过开发人心脏的2D和3D模型来模拟心脏组织中Thz波的波传播和热效应,从而扩展了Comsol多物理学中的现有计算模型©。这些模型有助于定义下一代生物医学设备中THZ辐射的安全限制,从而加速了无线网络的发展。