XiaoMi-AI文件搜索系统
World File Search System使用递归特征消除方法
摘要。情感识别是情感计算的一个分支,在过去几十年中引起了极大的关注,因为它可以实现更自然的脑部计算机界面系统。脑电图(EEG)已被证明是情绪识别的有效方式,可以跟踪和记录用户情感状态,尤其是对于原始的情感事件(例如唤醒和价值)。尽管已经显示出大脑信号与情绪状态相关,但提出的模型的有效性在某种程度上受到限制。挑战是提高准确性,同时适当提取有价值的功能可能是成功的关键。本研究提出了一个基于结合分形维度和递归特征消除方法的框架,以增强基于EEG的情绪识别的准确性。要提取和使用基于频谱的分形尺寸和基于光谱的特征,以更准确地识别。递归功能消除将用作特征选择方法,而情绪的分类将由支持向量机(SVM)算法进行。将使用广泛使用的公共数据库测试所提出的框架,与其他研究相比,结果有望证明其准确性和鲁棒性更高。这项研究的贡献主要是关于改善基于脑电图的情绪分类精度。潜在的限制对结果的通用性可能是不同的,因为不同的脑电图数据集可能会为同一框架产生不同的结果。因此,尝试不同的EEG数据集并测试替代特征选择方案对于将来的工作非常有趣。
基于块设计的脑电图实验中眼部伪影消除方法的比较
摘要:人们已经对眼球运动及其作为眼部伪影 (OA) 对脑电图 (EEG) 记录的贡献进行了深入研究。然而,它们的存在通常被认为会妨碍分析。一种被广泛接受的绕行方法是避免伪影。OA 处理通常简化为拒绝受污染的数据。为了克服数据丢失和行为限制,研究小组提出了各种校正方法。最先进的方法是数据驱动的,通常要求 OA 与大脑活动不相关。这对于视觉运动任务并不一定成立。为了防止相关信号,我们研究了一种双块方法。在第一个块中,受试者根据视觉引导范式进行扫视和眨眼。然后,我们为这些数据拟合了 5 种伪影去除算法。为了测试它们在伪影衰减和大脑活动保存方面的平稳性,我们在一小时后记录了第二个块。我们发现,扫视和眨眼仍可减弱到偶然水平,而休息试验期间的大脑活动仍可保留。
新冠疫情疫苗接种保护措施和控制等级
• 进行工作场所危害评估,以确定暴露风险 • 遵守适用的 OSHA 法规/标准 • 在选择危害消除方法时考虑 NIOSH 建议、CDC 指导和行业“最佳实践” • 在实施全面的感染控制时采用“控制层次结构”
基于利润的轨道交通行业仿真模型
4.1 模拟模型变量 ................................................................................................43 4.2 运输策略 ..............................................................................................................44 4.3 结果 – 个别实例 ..............................................................................................50 4.4 结果 – 模拟模型摘要 ......................................................................................63 4.5 回归分析 .............................................................................................................68 4.6 敏感性分析 – 利润边界 .............................................................................74 4.7 敏感性分析 – 燃料成本盈亏平衡点 .............................................................77 4.8 敏感性分析 – 延误时间 .............................................................................................80 4.9 利润损失 .............................................................................................................86 4.10 冲突消除方法...........................................................90 4.11 定价策略.................................................................................................101
开发过敏原食品作物的前景
食物过敏(FA)是一种食物敏感性,在全球范围内已成为关键的公共健康问题(Loh&Tang,2018)。fa描述了对人体可能发生的某些食物的不良免疫反应(Burks等,2012)。FA的流行率在近几十年来增加,挑战过敏者和食品科学家,以设计快速,准确的诊断测试,以及针对弱势群体的预防和治疗措施。fa已成为全球食品安全问题,除了免疫疗法脱敏(Du Toit等,2015)以及对过敏反应的使用使用肾上腺素。fa由于缺乏有效的过敏原消除方法而对敏感个体的生活产生负面影响。
开发不含过敏原的粮食作物的前景
食物过敏 (FA) 是一种食物敏感症,已成为全球严重的公共卫生问题 (Loh & Tang,2018)。FA 描述了人体对某些食物可能产生的不良免疫反应 (Burks 等人,2012)。近几十年来,FA 的患病率有所增加,对过敏症专家和食品科学家来说都是一个挑战,他们需要设计快速准确的诊断测试以及针对弱势群体的预防和治疗措施。除了通过免疫疗法脱敏 (Du Toit 等人,2015) 和使用肾上腺素注射治疗过敏反应外,缺乏可靠的预防措施,因此 FA 已成为一个全球食品安全问题。由于缺乏有效的过敏原消除方法,FA 对敏感个体的生活产生负面影响。
创新型直升机飞行噪音监测系统...
摘要:本文旨在全面阐述一种新的旋翼机噪音消除方法,特别是在飞行器接近地面且声学影响较大的终端程序期间。该方法致力于开发用于实时、飞行中监测发射噪音的技术和工具。声辐射的影响以简明、实用的形式呈现在一种新的驾驶舱仪表——飞行员声学指示器 (PAI) 上,用于执行更安静的操作。PAI 基于预先计算的声学数据的协同组合,这些数据与创新的非接触式测量系统收集的数据一起用于噪声估计算法,该系统能够获取主旋翼叶片运动。本文报告了当前在非稳定和准稳定气动声学预测以及翼尖-航向-平面攻角和推力系数观测方面的研究。本文讨论了新方法的结果以及 PAI 设计和开发过程的主要特点。
穆罕默德·费萨尔·西迪基博士
Siddiqui, MF、Reza, AW、Shafique, A.、Omer, H. 和 Kanesan, J. (2017)。使用预扫描和 Emaps 灵敏度的 FPGA 实现实时 SENSE 重建。磁共振成像,44,82-91。 Siddiqui, MF、Reza, AW 和 Kanesan, J. (2015)。用于脑 MRI 扫描分类的自动智能医疗决策支持系统。PloS one,10 (8),e0135875。 Siddiqui, MF、Mujtaba, G.、Reza, AW 和 Shuib, L. (2017)。使用计算机辅助诊断系统对脑 MRI 进行多类疾病分类。对称性,9 (37)。 Siddiqui, MF, Reza, AW, Kanesan, J., & Ramiah, H. (2014). 研究一种新型公共子表达式消除方法以实现低功耗和面积高效的 DCT 架构。《科学世界杂志》,2014 年。 Siddiqui, MF、Reza, AW、Omer, H. 等人 (2015)。参数化架构
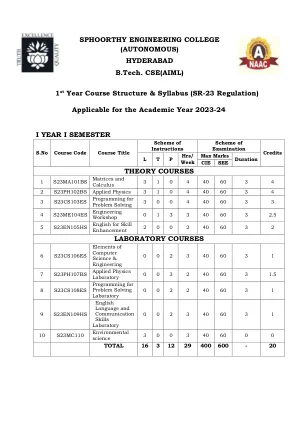
B. Tech(常规时间)的学术法规(R23)
单元I:矩阵矩阵的矩阵等级,由echelon形式,正常形式。cauchy – binet公式(无证明)。通过高斯 - 约旦方法的非奇异矩阵倒数,线性方程式系统,方程式的线性系统的一致性求解了均匀和非均匀方程的系统,高斯消除方法,雅各比和高斯·塞德尔迭代方法。ii二:特征值,特征向量和正交转换特征值,特征向量及其特性,对角度的对角线化,基质,Cayley-Hamilton定理(没有证明),Cayley-Hamilton Theorem,Quad theorem,Quad to y defuctation to y defuctation to y duiguctation y duiguctation y duiguctation y y y y y y dy fi y y y y y y y y y y y y y y y y y y y y y dy fiqur通过相似性转换,拉格朗日的减少和正交转换,复杂矩阵的类型(Hermition偏向Hermition&Unity)
5-syllabus-1700469682.pdf
单位 - I:通过梯形形式和正常形式的矩阵矩阵等级,高斯 - 约旦方法的非单个矩阵倒数,线性方程系统:求解高斯消除方法的均匀和非均匀方程的系统,高斯·塞德尔迭代方法。UNIT - II: Eigen values and Eigen vectors Linear Transformation and Orthogonal Transformation: Eigen values, Eigenvectors and their properties, Diagonalization of a matrix, Cayley-Hamilton Theorem (without proof), finding inverse and power of a matrix by Cayley -Hamilton Theorem, Quadratic forms and Nature of the Quadratic Forms, Reduction of Quadratic form通过正交转换为规范形式。单元-III:微积分平均值定理:Rolle的定理,Lagrange的平均值定理,其几何解释和应用,Cauchy的平均值定理,Taylor的系列。确定积分的应用在评估曲线旋转的表面区域和体积(仅在笛卡尔坐标中),不当积分的定义:beta和伽马功能及其应用。单位-IV:多变量计算(部分分化和应用)的定义极限和连续性。部分区分:Euler的定理,总导数,Jacobian,功能依赖性和独立性。应用程序: