XiaoMi-AI文件搜索系统
World File Search System牛顿镇计划与实施协议-NJ.GOV
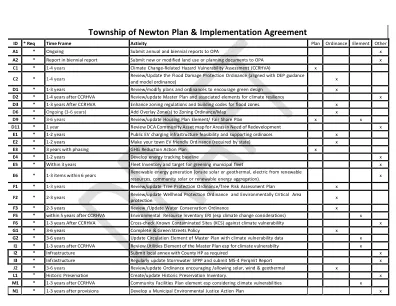
d1 * 1 - 3年的审查/修改计划和计划,以鼓励绿色设计X D2 * 1-4年,CCRHVA评论/更新的总体规划和有关气候弹性X D3 * 1-3年后,CCRHVA后增强了区域范围和建筑物代码的洪水区域后。x D6 * Ongoing (3-6 years) Add Overlay Zone(s) to Zoning Ordinance/Map x D9 * 3-6 years Review/update Housing Plan Element/ Fair Share Plan x x D11 * 1 year Review DCA Community Asset map for Areas in Need of Redevelopment x E1 * 1-2 years Public EV charging infrastructure feasibility and supporting ordinaces x E2 * 1-2 years Make your town EV friendly Ordinance (required by state) X E3 * 3年以相平进的降低动作计划X E4 * 1-2年在3年内开发能量跟踪基线X E5 *舰队清单和绿色市政舰队的目标X
牛顿-乔治国王大道第一阶段规划草案
一项环境研究表明,规划区的大部分地区受到生态价值高的鱼类水道的影响。建议修复水道及其周围的栖息地。这些区域可能包括自然公园和步道系统。当受影响的房产挂牌出售时,市政府将拨出资金购买部分房产。在其他情况下,当业主选择重新开发时,受影响的区域将由市政府保护。在所有情况下,业主都不会被迫搬迁或出售,现有建筑和房屋可以保留。
艾萨克·牛顿英语 (1643 1727) - 埃米兰格
关于数学,牛顿通常被认为是广义二项式定理的提出者,该定理对任何指数都有效。他发现了牛顿恒等式、牛顿法,对三次平面曲线(二元三次多项式)进行了分类,对有限差分理论做出了重大贡献,并且是第一个使用分数指标和采用坐标几何推导丢番图方程解的人。他用对数近似了调和级数的部分和(欧拉求和公式的前身),并且是第一个自信地使用幂级数和反转幂级数的人。他还发现了计算圆周率的新公式。
牛顿斯图尔特和米尼加夫地方计划 - ...
参与制定该地点规划的有: ● 当地社区:占总人口 4,000 人的 1,500 多人 ● 由邓弗里斯和加洛韦委员会、克里谷地区发展信托、克里谷社区委员会、第三部门总干事和牛顿斯图尔特倡议支持的当地指导小组 ● 自己的团队和社区代表组成,他们帮助指导了整个过程。他的声明旨在支持我们为牛顿斯图尔特和明尼加夫登记地点规划的意愿表达。本地方规划和本声明根据以下规定编制: ● 政府立法:2021 年城镇与乡村规划(地方规划)(苏格兰)条例 ● 苏格兰政府规划通告 1/2022:地方规划(LPP) ● 邓弗里斯和加洛韦议会的 LPP 要求概述。
迈克尔·A·牛顿 - 范德比尔特大学法学院
2018 年,在 Jean-Pierre Bemba 向国际刑事法院上诉分庭上诉的案件中作为辩护团队成员进行辩论 [包括导致完全无罪释放的简短准备] 以色列国家审计长的专家顾问 [评估以色列国防军在加沙的行动],2015-2018 年 在冈比亚诉缅甸案中向国际法院的冈比亚纪念馆提交专家报告,2020 年 10 月 ABA 国际刑事法院项目顾问委员会成员,http://www.aba-icc.org/ 成功谈判国际刑事法院《犯罪要素文件》的两名美国代表之一 – 1999 – 2001 年 [帮助就该文件达成共识] 伊拉克高等刑事法院司法分庭的国际法律顾问 2006 - 2009 年 [就杜贾尔审判、安法尔种族灭绝案以及其他案件的独立问题提供大量建议] 协调为联合国行为和纪律事务股提供支持,以调查和起诉联合国维持和平行动期间制服特遣队和文职人员犯下的广泛性别犯罪
基于牛顿-欧拉法的六旋翼飞行器运动方程研究
摘要 本文旨在设计和研究无人驾驶飞行器 (UAV) 六旋翼飞行器在三维空间中的动态模型。基于牛顿-欧拉法确定了导出的运动方程。这些方程具有非线性和耦合性。此外,为了使六旋翼飞行器具有真实的运动,模型中还嵌入了气动效应和扰动。六旋翼飞行器是一种垂直起降 (VTOL) 飞行器,具有悬停能力和灵活性,因此与固定翼飞行器相比毫不逊色。尽管如此,它的动态模型很复杂,被描述为不稳定的,并且不能在不扭转其轴的情况下进行平移运动。除了控制和仿真设计模块外,还通过 LabVIEW 软件建立了结论性数学模型。因此,对多个实验状态的稳定性进行了分析,以便提前展示用于平衡和轨迹跟踪的适当控制器。关键词:——无人机,六旋翼飞行器动力学,非线性控制,耦合和欠驱动模型,牛顿-欧拉方法。
财富信号PDF史蒂文·牛顿博士
●感觉皮层:空间和身体功能的歧视和识别。●颞叶(T3,T5):长期记忆,言语和阅读理解,情感价。●右颞叶(T4,T6):情感和身体意识,面部识别,音乐理解。●顶叶(P3,PZ,P4):听觉,视觉和动力学输入的整合。
太阳能电池参数的提取中的两个步骤和牛顿 - 拉夫森算法
Iterations -NRM - NRM -NRM -2SM -2SM -2SM 1 1 0.2 0.2 0.960466918 0.192093384 0.18449934 2 0.96986956 0.193973912 0.188129393 0.932816856 0.186563371 0.174029457 3 0.941324731 0.188264946 0.17721845 0.909783325 0.181956665 0.16554114 4 0.916395843 0.183279169 0.167956268 0.895021368 0.179004274 0.16021265 5 0.898535645 0.179707129 0.161473261 0.889732889 0.177946578 0.158324923 6 0.890477009 0.178095402 0.158589861 0.889104432 0.177820886 0.158101338 7 0.889125763 0.177825153 0.158108925 0.889092721 0.177818544 0.15809717173 8 0.889092734 0.177818547 0.17815470.1580971788888888888888888888988898888888988888888888888888888888888888888888889788889717177179797性小士范排别 0.177818543 0.158097171 9 0.889092715 0.177818543 0.158097171 0.889092715 0.177818543 0.158097171 10 0.889092715 0.177818543 0.158097171 Table 4 - Comparison of解决方程式的不同方法。6使用NRM和2SM。
经济发展实施计划-2023-2025
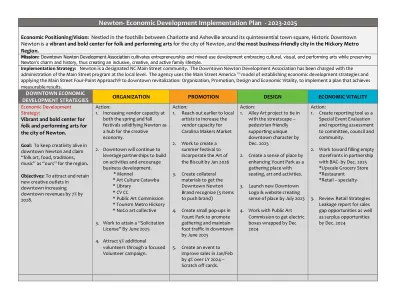
牛顿经济发展实施计划-2023-2025经济定位/愿景:牛顿市中心坐落在夏洛特和阿什维尔之间的山麓丘陵中,是牛顿市中心的历史悠久的牛顿市中心,是牛顿市的充满活力,大胆的民间和表演艺术中心,也是牛顿市,以及最富有商业友好的城市,是歇斯奇特的城市中最友善的城市。使命:牛顿开发协会市中心培养企业家精神和混合用途开发,在保留牛顿的魅力和历史的同时,采用文化,视觉和表演艺术,从而创造了一种包容,创造性和活跃的家庭生活方式。实施策略:牛顿是指定的NC Main Street社区。牛顿市中心开发协会已被指控在当地一级的主街计划管理。该机构使用Main Street American™模型来建立经济发展策略并将主要街道四点攻学®应用于市中心的振兴:组织,促进,设计和经济活力,以实现一项可衡量结果的计划。
23-3329
会开枪!我会得到你!最好杀了我!我要杀了你!” R. doc48-1,在1。牛顿军官用枪指着桑德斯,开始退后一,“一再大喊‘警察!下来!停止!放下它!您最好放下武器!放下枪!'” ID。桑德斯不遵守这些命令;取而代之的是,“他继续用手走向[牛顿军官],这是在他的夹克口袋里,抬起头,指着[牛顿军官],好像是枪。” ID。牛顿军官在命令时继续撤退。桑德斯(Sanders)“开始向[牛顿军官]冲刺,而他的手仍然在他的夹克口袋里,[牛顿军官]仍然在夹克口袋里冲刺,好像他有枪指着[他]。” ID。大约一两秒钟后,牛顿军官“在[桑德斯]五次释放了他的武器”。 ID。开火时,他距离桑德斯大约12到15英尺。牛顿军官在桑德斯摔倒后停止了射击。牛顿军官后来得知桑德斯没有武装。