XiaoMi-AI文件搜索系统
World File Search System图S1
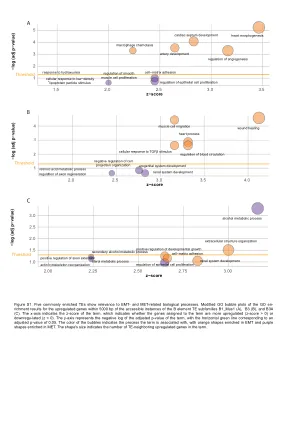
图S1。 五个通常富集的TE与EMT和MET相关的生物学过程相关。 在B1元素te subfamilies b1_mus1(a),b3(b)和b3a(c)的可访问实例的5000 bp内的GO富集结果的修改后的GO气泡图。 x轴表示该术语的z评分,该术语表明分配给该术语的基因是更上调的(z分数> 0)还是下降的(z <0)。 y轴表示该术语调整后的P值的负log,水平绿线对应于调整后的P值为0.05。 气泡的颜色表示该术语与之相关的过程,橙色形状富含EMT和紫色形状富含MET。 形状的大小指示了该术语中上调的基因的数量。图S1。五个通常富集的TE与EMT和MET相关的生物学过程相关。在B1元素te subfamilies b1_mus1(a),b3(b)和b3a(c)的可访问实例的5000 bp内的GO富集结果的修改后的GO气泡图。x轴表示该术语的z评分,该术语表明分配给该术语的基因是更上调的(z分数> 0)还是下降的(z <0)。y轴表示该术语调整后的P值的负log,水平绿线对应于调整后的P值为0.05。气泡的颜色表示该术语与之相关的过程,橙色形状富含EMT和紫色形状富含MET。形状的大小指示了该术语中上调的基因的数量。
量子图
量子图项目提议深入探索量子信息论核心的组合方面,它位于组合学和理论计算机科学与量子物理学的交叉点上。更具体地说,我们的项目旨在对量子图概念进行几项理论发展,量子图被视为图的非交换概括。这项跨学科的提案旨在开发新的组合和代数方法来解决量子信息中的基本问题,同时阐明组合结构和量子特性之间的深层关系。在量子信息论的框架内,量子图(也称为非交换图)的概念首次由 Duan 等人在 [DSW13] 中提出,目的是将香农理论中的某个概念推广到量子情况。与经典图可视为非自反对称关系这一事实类似,Weaver [Wea21] 将量子图表述为冯·诺依曼代数上的自反对称量子关系。Musto 等人 [MRV18] 还将有限量子图表述为有限量子集上的邻接运算符。非常令人惊讶的是,这三种不同的观点指向了同一个对象,即量子图,这是本博士项目的重点。
机器图
我向作者 P. Kannaiah 博士、K.L. 教授表示祝贺。S.V.U. 的 Narayana 和 K. Venkata Reddy 先生。蒂鲁帕蒂工程学院出版了这本关于“机械制图”的书。本书首先介绍了工程制图的基础知识,然后作者系统地介绍了机械制图。在我看来,这是一种极好的方法。这本书对机械工程专业文凭、学位和 AMIE 级别的学生来说都是一本宝贵的书。P. Kannaiah 博士拥有约二十五年的丰富教学经验,这些经验得到了充分利用,正确地反映了对该主题的处理和呈现。K.L. 教授机械工程教授 Narayana 和车间主管 K. Venkata Reddy 先生明智地联手,从他们丰富的经验中提供有用的插图,这一独特之处是本书的一大财富,其他书籍可能没有这样的机会。任何绘图书都必须遵循 BIS 标准。作者在这方面做得非常细致。此外,本书毫无遗漏地涵盖了印度各大学的教学大纲。学习绘图原理并将其应用于工业实践对任何学生来说都是必不可少的,本书是工程专业学生的宝贵指南。它也是工业设计和绘图部门的参考书。本书几乎是机械绘图的完整手册。本书是学生和专业人士学习计算机图形学的基础,计算机图形学是现代的必备课程。我相信工程专业的学生会发现这本书对他们非常有用。
研究GPNMB在缺陷型巨噬细胞中的作用和调节
Title: Investigating the Role and Regulation of GPNMB in Progranulin-deficient Macrophages Authors: Drew A. Gillett 1,2,3 , Noelle K. Neighbarger 1,2,3 , Cassandra Cole 1,2,3 , Rebecca L. Wallings 1,2,3# , and Malú Gámez Tansey 1,2,3,4#* 1 Department of Neuroscience, University佛罗里达州盖恩斯维尔,佛罗里达州佛罗里达州2佛罗里达大学盖恩斯维尔大学神经退行性疾病转化研究中心3佛罗里达大学麦克奈特脑研究所,佛罗里达州盖恩斯维尔市4诺曼·菲斯维尔神经病学院,佛罗里达州盖恩斯维尔,佛罗里达州盖恩斯维尔,佛罗里达,#Conconcontibed #conconcontributed#Concontaluted#Concontaled *均等 *MalougámezTansey,Ph.d.d.d.d.d.d.d.d.d.d.d.d. ph.d.d.d.d.d.d。 mgtansey@ufl.edu摘要
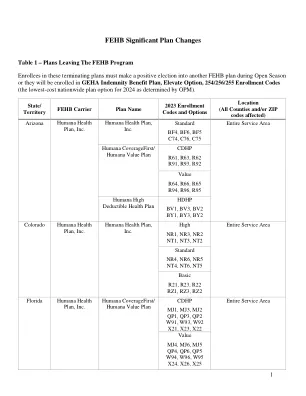
FEHB 重大计划变更
城市:奥尔迪、亚历山大、安纳代尔、阿什本、比尔顿、本顿维尔、贝里维尔、布鲁蒙特、博伊斯、布里斯托、布罗德伦、布鲁克、伯克、卡尔弗顿、卡萨诺瓦、卡瑟平、卡特莱特、森特维尔、尚蒂伊、克利夫顿、德拉普兰、杜勒斯、邓弗里斯、邓恩洛林、费尔法克斯站、福尔斯彻奇、贝尔沃堡、弗雷德里克斯堡、弗兰特罗亚尔、堡。迈尔、盖恩斯维尔、加里森维尔、戈尔德维恩、大瀑布城、格林韦、汉密尔顿、哈特伍德、干草市场、赫恩登、休姆、利斯堡、林肯、林登、洛顿、洛维茨维尔、马纳萨斯、马克姆、马歇尔、麦克莱恩、梅里菲尔德、米德尔堡、米德尔敦、米德兰、米尔伍德、弗农山、纽因顿、诺克斯维尔、奥克顿、奥科克恩、奥尔良、派奥尼安斯普林斯、巴黎、帕特洛、菲尔蒙特、珀塞尔维尔、匡蒂科、雷克托敦、雷明顿、雷斯顿、朗德希尔、鲁比、萨默维尔、斯普林菲尔德、斯特林、萨默达克、平原、索恩堡、三角区、上维尔、维也纳、沃伦顿、沃特福德、西麦克莱恩、怀特波斯特和伍德布里奇