XiaoMi-AI文件搜索系统
World File Search System相浦
LNM信息技术研究所，斋浦尔
The LNM Institute of Information Technology, Jaipur (Deemed-to-be-University) Gram – Rupa Ki Nangal, Post – Sumel, Via – Jamdoli, Jaipur – 302031, Tel: +91-141-5191741, 5191757, Fax: +91-141-5189214, 2689014 E-mail: info.lnmiit@lnmiit.ac.in，网站：www.lnmiit.ac.in
LNM信息技术研究所，斋浦尔
The LNM Institute of Information Technology, Jaipur (Deemed-to-be-University) Gram – Rupa Ki Nangal, Post – Sumel, Via – Jamdoli, Jaipur – 302031, Tel: +91-141-5191741, 5191757, Fax: +91-141-5189214, 2689014 E-mail: info.lnmiit@lnmiit.ac.in，网站：www.lnmiit.ac.in
![[3965] - 127 P1374 - 浦那大学](/simg/7\76c20e194b543edacec5968c98b13d1e55859a42.webp)
[3965] - 127 P1374 - 浦那大学
考虑 CYG 活动出席人数的具体示例。事实包括出席人数、门票销售价值。维度包括 CYG 年份、场地、运动项目、类型（普通比赛、半决赛、决赛）、男子/女子。场地按位置和建筑类型分为中央封闭式、中央开放式、远程式。运动项目细分为各种活动。
![[3665]-162 P1702 - 浦那大学](/simg/a\abcac0aa15bf15b2b5c24f92bddaf9b1eefdbe42.webp)
[3665]-162 P1702 - 浦那大学
问题总数：10] [总页数：3 [3665]-185 M.E.(生产) 软硬件自动化 (旧版及 2002 年修订版课程) 时间 ：3 小时] [最高分数 ：100 考生须知：1) 回答每部分中的任意三个问题。2) 回答第一部分中的 3 个问题和第二部分中的 3 个问题。3) 两部分的答案应分别写在不同的书中。4) 必要时必须绘制清晰的图表。5) 右侧的数字表示满分。6) 您的答案将作为一个整体进行评估。7) 允许使用对数表、计算尺、莫里尔图表、电子袖珍计算器和蒸汽表。8) 必要时，假设合适的数据。
麻省理工学院艺术设计与技术大学（浦那）
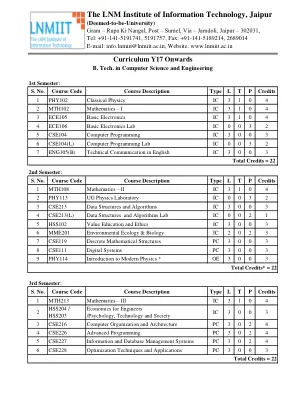
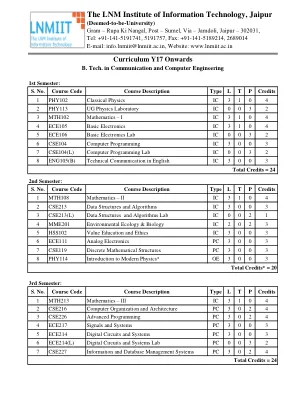
在麻省理工学院 ADT 大学，导师-学徒计划在促进学生福祉和学业成功方面发挥着至关重要的作用。这些计划旨在解决学业挑战和心理需求，为学生营造一个支持性的环境。以下是详细介绍各学院 2022-23 学年和 2023-24 学年的导师-学徒计划的文件链接，突显了大学致力于通过有效的指导来培养学生的发展。
LNM信息技术研究所，斋浦尔
The LNM Institute of Information Technology, Jaipur (Deemed-to-be-University) Gram – Rupa Ki Nangal, Post – Sumel, Via – Jamdoli, Jaipur – 302031, Tel: +91-141-5191741, 5191757, Fax: +91-141-5189214, 2689014 E-mail: info.lnmiit@lnmiit.ac.in，网站：www.lnmiit.ac.in
NASA SBIR-2024-相1招标
3实现航空技术目标。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.11 3.1航空技术主题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.13保护航空旅行者和公众（目标2.1）。。。。。。。。。。。。。。。。。。。。.14保护环境（目标2.2）。。。。。。。。。。。。。。。。。。。。。。。。。。。。.16提高容量和流动性（目标2.3）。。。。。。。。。。。。。。。。。。。。。。。.18国家安全伙伴关系（目标3.1）。。。。。。。。。。。。。。。。。。。。。.20探索革命航空概念（目标10.5）。。。。。。。。。。。.22 3.2太空启动计划主题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.25国家安全伙伴关系（目标3.1）。。。。。。。。。。。。。。。。。。。。。.26保证国际空间站访问（目标8.1）。。。。。。。。。。。。。。.28任务安全和可靠性（目标8.2）。。。。。。。。。。。。。。。。。。。。。。。。.30 3.3任务和科学测量技术主题。。。。。。。。。。。。。。。。。.33任务风险分析（目标10.1）。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。.34科学和工程驱动的架构和技术（目标10.2）。。。。。。。。。。。。。。。。。。。。。。。。。。。.36 3.4创新技术转移伙伴关系主题。。。。。。。。。。。。。。。。。。。.39向社会扩大利益（目标3.3）。。。。。。。。。。。。。。。。。。。。。。。。。.40 NASA技术的新来源（目标10.3）。。。。。。。。。。。。。。。。.42 3.5企业对代理教育和推广目标的贡献。。。。。。。.45支持NASA教育目标（目标6）。。。。。。。。。。。。。。。。。。。。。。。.45支持公共外展目标（目标7.1）。。。。。。。。。。。。。。。。。.48
量子场论中的Berry相
𝑚 ത 𝜓𝑒 𝑖𝛾 01 𝛼 𝜓= 𝑀 ത 𝜓 + 𝜓 − + hc 该理论具有 𝑈1 𝑉 对称性 𝜓→𝑈𝜓 。 • 𝑀≠0 ：具有唯一基态的间隙。 • 𝑀= 0 ：余维数为 2 的无间隙魔鬼点。 • 𝑀= 0 ：对于 𝑈1 𝐴 −𝑈1 𝑉 出现混合异常，但对于 𝑀≠0 则不存在 𝑈1 𝐴 问：我们可以添加相互作用来使系统间隙化，同时仅保留 𝑈1 𝑉 对称性吗？ （否。 Diabolic point 受 Thouless 泵不变量保护。）问：是否存在连续依赖于参数的平凡间隙界面族？（否，Berry 相的体边界对应示例）
