XiaoMi-AI文件搜索系统
World File Search System“今年春节人人都有礼物”活动规则 - Viettel Telecom
1.促销期:2024年1月15日-2024年3月15日 2.参与者 - Viettel 预付费移动用户在促销期间通过发送短信 KM 至 191 成功注册预付费移动组合套餐。- Viettel 的 FTTH 订阅包括: + 促销期间 FTTH 服务的新客户(成功接受)。+ FTTH客户成功升级到比原价格更高的套餐(促销期间套餐升级时间。- Viettel 的电视订阅包括: + 移动用户在促销期间在 TV360 服务上新注册标准、VIP K+ Mobile、VIP K+ HD、K+SD、HBO GO 套餐(套餐 1、3、6、9、12 个月)。+ 客户在促销期间在可用的互联网服务上新注册 Viettel 的 TV360 电视服务或同时使用 STD、STDBOX、VKP、VKPBOX 套餐注册电视服务和互联网服务。3.计划政策 3.1 注册服务套餐时累积 5% Viettel++ 积分的计划 - 当客户成功加入/注册服务/套餐时,按每月实际价格累积 5% Viettel++ 消费积分,积分仅限于 N+1 月的最后一天(N 为赚取积分的月份)。- 每个成功交易的客户在整个计划实施期间只能获得1次/服务。3.2 抽奖活动
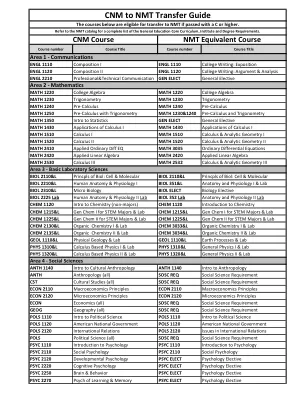
CNM 至 NMT 转机指南
BIOL 2110&L 生物学原理:细胞与分子 BIOL 2110&L 生物学原理:细胞与分子 BIOL 2210&L 人体解剖学与生理学 I BIOL 351&L 解剖学与生理学 I 与实验室 BIOL 2310&L 微生物学 BIOL ELECT 生物学选修课 BIOL 2225 实验室 人体解剖学与生理学 II 实验室 BIOL 352 实验室 解剖学与生理学 II 实验室 CHEM 1120 化学概论(非专业) CHEM 1120 化学概论 CHEM 1215&L 面向 STEM 专业的普通化学 I 与实验室 CHEM 1215&L 面向 STEM 专业的普通化学 I 与实验室 CHEM 1225&L 面向 STEM 专业的普通化学 II 与实验室 CHEM 1225&L 普通化学II 面向 STEM 专业及实验室 CHEM 2130&L 有机化学 I 与实验室 CHEM 3033&L 有机化学 I 与实验室 CHEM 2135&L 有机化学 II 与实验室 CHEM 3034&L 有机化学 II 与实验室 GEOL 1110&L 物理地质学与实验室 GEOL 1110&L 地球过程与实验室 PHYS 1310&L 基于微积分的物理学 I 与实验室 PHYS 1310&L 普通物理学 I 与实验室 PHYS 1320&L 基于微积分的物理学 II 与实验室 PHYS 1320&L 普通物理学 II 与实验室
Biostatistics -Ms.pdf -GMU目录
除了满足研究生学习的一般入学要求外,所有申请人还具有基本的计算机素养。他们必须拥有一个领域的认可机构的学士学位,其中包括微积分的一年课程,以及在Matrix或线性代数的一个学期课程。在数学,统计和某些工程计划等领域具有学位的申请人通常符合这些要求。对于其他领域学位的申请人,如果学生成功地完成了相当于梅森课程的课程,通常会满足这些要求。
辐射光子环境的精确量子电动力学的补充信息
定义了整个积分的每个极点z z z z z z z z z 7n的sudoModes vvξn(r),并在给定的一组模式索引ξ中由n索引。使用残基定理是一个合理的假设,因为对于t≥0的∂t〜c 0(t)是连续的,这是等式中k的积分。11必须对所有τ≥0收敛,因此R∞0dkρ(k)g2ξ(k,r)收敛。此外,人们期望足够大的r,r'的行为是术语∝ exp( - ik(cτ±r))的组合,该术语对应于传入波或即将波动的空间成分。将整数分成这些组件产生的术语会在上半层中收敛。我们以这种方式对下面的球形介电粒子执行积分,我们发现一半平面收敛条件会产生步骤函数θ(τ -∆ t(r,r,r'))τ>0。时间延迟∆ t(r,r')是光通过纳米颗粒从r传播到r'的时间,并且通常取决于其几何形状。在下面的第六节中,我们显示了如何在等式中出现的下限k = 0的积分。10可以以与等式的分析方式评估。12通过识别积分的对称和反对称部分。我们讨论了第六节末尾的较低集成极限扩展到-∞的含义。
机械工程 - MECH
MECH 5330 生物力学工程概论 (3) LEC. 3. Pr. MECH 2140 和 MECH 3120 和 MECH 2130。介绍多学科研究领域生物力学工程 - 基于力学和微积分的生物系统内能量和力以及这些能量和力产生的物理效应。涵盖的主题包括 1) 人体肌肉骨骼生理学和解剖学、2) 生物材料力学、3) 生物力学相关刚体动力学、4) 技术工程和生物力学系统应用、5) 医学成像技术以及 6) 生物力学工程研究的应用。
MATH1020-微积分和线性代数II-单位指南
单元描述Math1010中引入的线性代数和微积分的基础进一步探索和扩展。用代数涵盖的主题包括:反矩阵,决定因素,矢量空间和子空间,特征值以及特征向量以及线性变换。在微积分中,主题包括:限制,连续性和衍生物,数值集成,多项式,序列和序列和微分方程的进一步发展。另外,引入了两个或多个变量的复数和计算。学生在整个课程中都利用数学软件来支持和加强解决各种理论和实际问题的问题。
准确解决的平面差异系统...
近年来在二阶非线性普通差方程的研究中取得了迅速的进步。这些方程中的某些方程式特别有趣,因为它们在其他科学领域频繁出现。作为示例,我们可以引用li´enard方程[17,35],瑞利方程[37]和自治系统,导致这些类型的方程(例如Kukles的系统[5,19]和Kolmogorov System [36])。然而,在研究这些非线性差方程和系统的研究中,重要的挑战之一是确定哪些是可以集成的。这可以通过研究可集成性来实现,这可以从解决方案中明确收集所有必要的数据,也可以从不变的第一个积分,逆积分因子和不变的代数曲线等中隐含地收集。我们记得,如果n -1独立的第一个积分具有n -1个独立的第一个积分,则维度n的自主差异系统是完全可以集成的,因此可以通过与这些第一个积分的水平集相交(有关更多详细信息,请参见[9,28])。对于平面差异系统,对第一个积分的知识在研究其动力学行为中至关重要。已经提出了几种分析方法来解决可集成性,每种方法都有其自身的优势和缺点。这些方法包括Noether对称性[34],Lie对称性[32,6],Darbouxian的综合性理论[14],直接方法[21,22]和Painlev´e分析[7,13]。作为最后一种方法的一个特别有趣的例子,Nucci和Leach [31]提出了一种由x = - βxy -µx +γy + µk表达的传染病模型,