XiaoMi-AI文件搜索系统
World File Search System高灵敏度非线性识别,用于追踪柔性结构中的早期疲劳迹象
本研究描述了一种基于物理和数据驱动的非线性系统识别 (NSI) 方法,用于检测由于振动载荷造成的早期疲劳损伤。该方法还允许实时跟踪损伤的演变。几何刚度、立方阻尼和相角偏移等非线性参数可以根据疲劳循环进行估算,这已通过实验使用暴露于振动的柔性铝 7075-T6 结构进行了证明。NSI 用于创建和更新非线性频率响应函数、主干曲线和相位轨迹,以可视化和估算结构健康状况。研究结果表明,动态相位对早期疲劳损伤的演变比几何刚度和立方阻尼参数等非线性参数更为敏感。引入了一种改进的 Carrella - Ewins 方法,从非线性信号响应计算主干,这与数值和谐波平衡结果高度一致。提出了相位追踪方法,该方法似乎可以在疲劳寿命的大约 40% 后检测到损伤,而几何刚度和立方阻尼参数能够在生命周期的大约 50% 后检测到疲劳损伤。[DOI:10.1115/1.4052420]
纸晶体结构工作表答案
任务是解释一组与化学相关的问题,涉及晶体结构,包装因子,配位数,密度和晶格参数。1)对于以面部为中心的立方金属,通过考虑球的体积(原子)来得出并计算包装因子。回想一下,半径为“ r”的球体的体积由(4/3)πr³给出。2)NaCl和CSCL都是以面部为中心的立方结构。确定NaCl中Na和NaCl中CL的配位数,考虑到其离子半径:116 pm钠的钠和氯化物的167 pm。3)使用其公式的重量(58.44 g/mol)和晶格常数(5.640Å)来计算NaCl的密度。4)确定以人体中心结构的钨的配位数,因为其共价半径(单键)为137 pm。5)使用公式:ρ=(n×m) /(a³×n_a)6)基于其晶体结构和原子质量(183.84 g / mol)来计算钨的密度,鉴于tantalum的边缘长度为0.330 nm,从该信息中计算出该信息,并在该信息中计算出tantalum的边缘长度。7)黄金的晶体结构是以面部为中心的立方体,密度为19.3 g/cm³。使用它来确定其晶格常数(a)。8)计算银的面部中心立方单元的边缘长度,因为其半径为9.09 x 10^-11 m,密度为10.5 g/cm³。9)polonium采用简单的立方结构,而其他则是离子的。在PM中确定其单位电池边缘的长度。13)石墨烯是由常规的SP²杂交碳原子建造的二维晶格。10)如果氧化镁具有面部为中心的立方结构,其原子半径为mg(65 pm)和O(140 pm),密度为3.58 g/cm³,则计算其晶格常数(a)。11)鉴于氟化钙CAF2具有FCC Bravais晶格,并且在分数坐标处的Origin和F的CA基础上,绘制了该结构的一个常规立方单元。12)确定晶格常数为5.451Å,确定从Ca原子到A埃原子的距离。确定其Bravais晶格并绘制Wigner-Seitz原始单位单元。14)计算石墨烯中最近的邻居原子之间的距离,该原子给出为0.14 nm。15)编写基础向量,以描述石墨烯单位单元中原子的位置,首先是在绝对位置(具有X和Y-Components和Angstroms中的距离),然后在分数坐标中。应使用常规晶格向量表示分数坐标的原子位置,该量子与原始晶格向量相吻合。对于带有空间群227的晶体,通过考虑以下几个方面来确定其点组和Bravais晶格:首先,根据空间组允许的对称操作确定点组;其次,根据空间群是否与原始晶格或非主要晶格兼容,建立原始或居中的Bravais晶格的类型。
马拉维冷链和 COVID-19 疫苗分发规划
为了确定马拉维疫苗 PQS 冷链中每个商店和设施的产能利用率,我们使用了基于 EPI 计划所需的疫苗数量(例如,疫苗和每种疫苗所需的剂量);规定的分发时间表(例如,每月分发到设施级别和地区);每个设施和地区的目标人群;以及疫苗特性(小瓶大小、每剂立方升、浪费率、缓冲库存)。这是根据设施中可用且运行良好并用于疫苗的 PQS 批准 CCE 的总净立方升来评估的。如果使用了 10-80% 的容量,则将利用率类别定义为适当;未充分利用
通过中央力量的连续变化纠缠
我们描述了一种完整的方法,用于精确研究附近两个量子质量之间的重力相互作用。由于这些质量的位移比其中心之间的初始分离小得多,因此位移与分离比是一个纳特参数,可以扩展引力范围。我们表明,仅当系统演变为非高斯状态时,即至少在至少扩展到立方术语时,在这种实验中的范围对INILIAL相对动量敏感。表现出了力梯度作为位置摩托米相关性的主要贡献者的关键作用。 我们为纠缠增益建立了封闭形式的表达,这表明立方术语的贡献与动量成正比,而四分之一的术语与动量平方成正比。 从量子信息的角度来看,结果发现应用是非高斯纠缠的动量见证人。 我们的方法用途广泛,并适用于任何数量的中央交互。表现出了力梯度作为位置摩托米相关性的主要贡献者的关键作用。我们为纠缠增益建立了封闭形式的表达,这表明立方术语的贡献与动量成正比,而四分之一的术语与动量平方成正比。从量子信息的角度来看,结果发现应用是非高斯纠缠的动量见证人。我们的方法用途广泛,并适用于任何数量的中央交互。
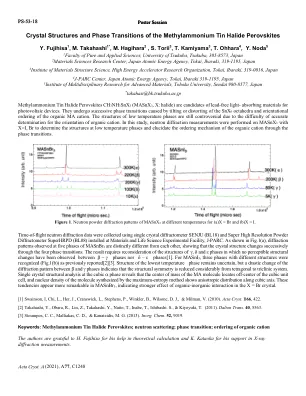
甲基铵锡卤化物钙钛矿的晶体结构和相变
使用安装在 J-PARC 材料与生命科学实验设施的单晶衍射仪 SENJU (BL18) 和超高分辨率粉末衍射仪 SuperHRPD (BL08) 收集飞行时间中子衍射数据。如图 1(a) 所示,在 MASnBr 3 的五个相中观察到的衍射图案彼此明显不同,表明晶体结构通过四个相变依次变化。该结果需要重新考虑 g、d 和 e 相的结构,其中 b - g 相和 d – e 相之间没有观察到明显的结构变化[1]。对于 MASnI 3 ,如先前报道的那样[2][3],识别出三个具有不同结构的相(图 1(b))。最低温相的结构仍然不确定,但 b 相和 g 相之间衍射图案的剧烈变化表明结构对称性从四方晶系到三斜晶系显著降低。立方a相单晶结构分析表明MA分子的质心位于立方晶胞中心之外,用最大熵法合成的分子核密度沿立方轴呈现各向异性分布。这些趋势在MASnBr 3 中表现得更为明显,表明X = Br晶体中有机-无机相互作用的影响更强。
3D 打印介电晶体的有效介电常数测量
摘要 — 增材制造为创新天线和微波元件提供了新的可能性。为了充分发挥其潜力,必须充分利用 3D 打印技术提供的功能。3D 打印结构化电介质目前在这方面受到广泛关注。然而,表征这种晶体结构的介电性能并不容易,而且经常需要对这种性能做出假设。本文展示了在具有不同填充率的简单立方 (SC) 和面心立方 (FCC) 晶体几何中,增材制造结构化电介质的介电常数和损耗角正切的表征。将测量结果与 Maxwell-Garnett 有效介质近似预测的值以及从长波长极限的三维平面波展开法 (PWEM) 中提取的有效折射率进行了比较。
4H-SiC中高N原子密度层结构及各向异性的第一性原理研究
位点(六边形 h 或准立方 k)。Si(0) 表示不与 NC 原子相邻的 Si 原子数;而 Si(1) 和 Si(2) 分别表示与一个和两个 NC 原子相邻的 Si 原子数。
利用氮空位进行量子信息处理...
图 1:钻石面心立方结构内的 NV 缺陷。NV 中心由碳晶格(黑色)中空位(白色)旁边的氮取代基(蓝色)组成。量子化轴可以以相等的概率位于四个晶体取向之一。