XiaoMi-AI文件搜索系统
World File Search SystemCSC 311:机器学习简介 - 讲座1
•线性代数:向量操作,矩阵乘法/裁定量/痕迹/特征值)•微积分:部分导数/梯度。•概率:共同分布(高斯,指数,伯努利,多变量正常);贝叶斯规则。•统计:期望,方差,协方差,中位数;最大似然。•数值优化:最大化功能,最小化功能,最大值,最小值;最大似然。
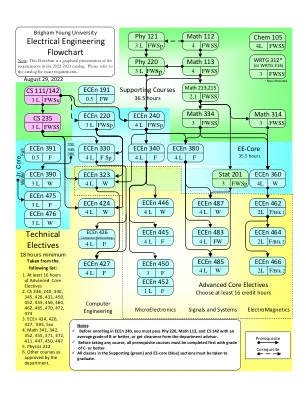
电气工程流程图技术选修课
要求1:完成22门课程。 CS 1 11 - 计算机科学概论 3.0 CS 235 - 数据结构和算法 3.0 EC EN 191 - 新生研讨会 0.5 EC EN 220 - 数字系统基础 3.0 EC EN 240 - 电路分析与实验室 4.0 EC EN 330 - 嵌入式系统编程简介 4.0 EC EN 340 - 电子电路设计 1 4.0 EC EN 360 - 电磁场与波 4.0 EC EN 380 - 信号与系统 4.0 EC EN 390 - 初级团队设计项目 3.0 EC EN 391 - 初级研讨会 0.5 EC EN 475 - 顶点设计 1 3.0 EC EN 476 - 顶点设计 2 3.0 MATH 112 - 微积分 1 4.0 MATH 113 - 微积分 2 4.0 MATH 213 - 小学线性代数 2.0 MATH 215 - 计算线性代数 1.0 MATH 314 - 多元微积分 3.0 MATH 334 - 常微分方程 3.0 PHSCS 121 - 牛顿力学概论 3.0 PHSCS 220 - 电磁学概论 3.0 STAT 201 - 工程师和科学家统计学 3.0
利用量子机器学习区分量子态
摘要 — 量子机器学习 (QML) 算法在机器学习 (ML) 领域具有重要意义,因为它有望在执行基本线性代数子程序 (BLAS) 时实现量子加速,而基本线性代数子程序是大多数 ML 算法的基本元素。通过利用 BLAS 操作,我们提出、实现并分析了一种时间复杂度低至 O (NKlog (D) I/C) 的量子 k 均值 (qk-means) 算法,以将其应用于判别读出时量子态的基本问题。判别量子态允许从低级同相和正交信号 (IQ) 数据中识别量子态 | 0 ⟩ 和 | 1 ⟩,并且可以使用自定义 ML 模型来完成。为了减少对传统计算机的依赖,我们使用 qk-means 在 IBMQ Bogota 设备上执行状态鉴别,并设法找到高达 98.7% 的分配保真度,仅略低于 k-means 算法。检查将两种算法应用于量子态组合所产生的分配保真度分数,结果与我们使用 Pearson 相关系数的相关性分析一致,其中证据表明,在所分析的设备上,(1, 2) 和 (2, 3) 相邻量子比特对之间存在串扰。索引术语 — 量子计算、机器学习、量子机器学习、K-Means、QK-Means、串扰
量子力学:从基础到高...
对线性代数,复数理论,概率理论,傅立叶变换,近极空间,量子力学,极化和光子概念的假设,量子测量,量子干涉法,量子密码学的基础知识,BB84协议,量子的基础原理,量子的基础,量子算子,量子不确定,量子不确定性,量子不确定,量子,EPR ker nocter,Epr spare,量子计算,量子通信和量子传送的基础知识,量子中继器,谐波振荡器的量化,量子隧道,统一操作员,投影操作员,量子电路,量子编程。对线性代数,复数理论,概率理论,傅立叶变换,近极空间,量子力学,极化和光子概念的假设,量子测量,量子干涉法,量子密码学的基础知识,BB84协议,量子的基础原理,量子的基础,量子算子,量子不确定,量子不确定性,量子不确定,量子,EPR ker nocter,Epr spare,量子计算,量子通信和量子传送的基础知识,量子中继器,谐波振荡器的量化,量子隧道,统一操作员,投影操作员,量子电路,量子编程。
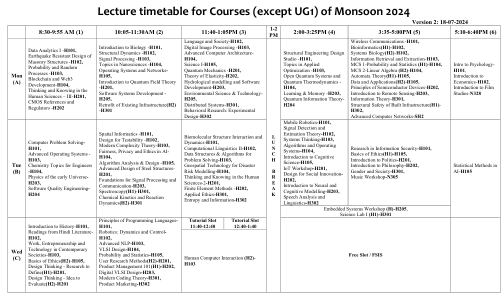
2024 年季风课程(UG1 除外)的讲座时间表
无线通信 - H101、生物信息学 (H1) - H102、系统生物学 (H2) - H102、信息检索与提取 - H103、MCS 1-概率与统计 (H1) - H104、MCS 2-线性代数 (H2) - H104、自动机理论 (H1) - H105、数据与应用 (H2) - H105、半导体器件原理 - H202、遥感简介 - H203、信息理论 - H301、建筑基础设施结构安全 (H1) - H302、高级计算机网络 - SH2
物理学作为信息处理课程大纲
本课程将介绍量子信息理论 (QIT) 的形式化方法,并展示它们与经典信息理论的关系。这些方法将用作思维工具,而不是计算工具。量子理论或统计物理学的背景将很有用,但不是必需的;基础物理学和对线性代数(向量和运算符)的熟悉将很有帮助。我们将讨论各种抽象概念,但重点是它们的直观含义,而不是它们的形式结构。不需要编码,但任何有此倾向的人都会看到许多模型构建的机会。
物理323-量子力学I
•教科书 - 强烈建议本课程使用教科书。本课程的教科书用于参考材料;教科书中不会分配家庭作业问题。量子力学是这种量子力学水平的优点。gri ths for量子力学简介是一本可接受的教科书,但错过了许多形式。我们将使用线性代数比刻板的代数要多。Sakurai的现代量子力学是一本很棒的教科书,但其方法可能太正式了 - 这是为研究生院做准备的好文字。
量子计算和信息科学专业培训计划:2周(2025年2月17日至2025年2月28日)第1周:
类型,字符串,操作员和表达式等,控制流说明,数据结构:列表,词典,元组,功能和模块等。第2周:量子力学和线性代数的叠加,纠缠,Young的双缝实验,状态空间,量子测量,线性操作员和矩阵,Pauli矩阵,内部产品,特征向后传播器和特征值等量子门和电路单/多量子门,量子电路,铃 div>
Biostatistics -Ms.pdf -GMU目录
除了满足研究生学习的一般入学要求外,所有申请人还具有基本的计算机素养。他们必须拥有一个领域的认可机构的学士学位,其中包括微积分的一年课程,以及在Matrix或线性代数的一个学期课程。在数学,统计和某些工程计划等领域具有学位的申请人通常符合这些要求。对于其他领域学位的申请人,如果学生成功地完成了相当于梅森课程的课程,通常会满足这些要求。
数学495QC量子计算秋季2025
本课程将介绍本科生的基础量子计算和拓扑量子计算。该课程被设计为自我包含。我们将从布尔逻辑,线性代数以及量子力学的公理和基础的基础开始。然后,我们将进入旋转,单一矩阵和量子门。作为一种应用程序,我们将讨论算法,例如Shor的算法和RSA加密。我们希望使用Anyons涵盖拓扑量子计算,并且时间是否允许进一步的主题。这为该领域的工作提供了坚实的背景。