XiaoMi-AI文件搜索系统
World File Search System表面声波中的费米子量子信息
量子计算机即将为现代技术带来革命,为科学家提供无与伦比的计算资源。借助叠加原理和纠缠等量子力学现象,这些计算机可以解决某些计算问题,而这些问题即使是最强大的传统超级计算机也无法解决。阻碍这场计算革命的主要挑战之一是对量子比特的精确控制。量子系统极其脆弱,从本质上讲,如果不破坏其量子态,就无法对其进行测量。我编写了一个数值程序来求解时间相关的薛定谔方程,这是一个描述波函数演化的微分方程。我的代码相对于其他求解器的优势在于速度。我使用了图形处理单元 (GPU),这是一种最近才成熟的技术,可以加速高性能计算。硬件加速使我能够在几天内而不是几年内解决复杂的时间演化问题。如此出色的加速使我能够计算半导体器件中单个电子的行为。电子特别有趣,因为它们在现代技术中无处不在,而且是基本的量子粒子。使用我的代码生成的模拟,我跟踪了电子波函数在量子电路中传播时的时间演变。通过动画呈现波函数的演变,我能够直观地看到电子在空间和时间中传播的波函数。这是研究纳米器件中量子粒子行为的出色工具。我的论文重点关注实验室中现成器件的实际建模或可在不久的将来制造的设计。我首先将单个电子建模为量子比特。我给出了最佳量子比特的定义,并列出了操纵电子携带的量子信息所需的操作集。
利用流动表面声波声子进行量子通信 1
图 2. 声子介导的量子态转移和过程层析成像。a 测量的 Q 1 激发态群体 PQ 1 e 与时间和 Q 1 裸频率的关系,耦合器 G 1 处于中间耦合 κ 1 / 2 π = 2.4 MHz(在 3.976 GHz 处测量),G 2 设置为零耦合。在这种配置中,Q 1 的能量弛豫主要由通过 UDT 1 的声子发射主导,其次是行进声子动力学。白色和红色虚线分别表示单向和双向工作频率(见正文);插图显示量子位激发和测量脉冲序列。b 通过行进声子在单向(左)和双向(右)工作频率下进行量子态转移。与单向传输相比,双向传输的 Q 2 的最终群体要小 4.5 倍,这与模拟结果一致。绿色实线来自主方程模拟。插图:脉冲序列。对于任一过程,Q 1 的发射率均设为 κ uni | bi c / 2 π = 10 | 6 MHz,对应于 81 | 138 ns 的半峰全宽 (FWHM) 声子波包。c 单向和双向区域的量子过程层析成像,过程保真度分别为 F uni = Tr ( χ exp · χ ideal ) = 82 ± 0 . 3 % 和 F bi = 39 ± 0 . 3 %。红色实线显示理想传输的预期值;黑色虚线显示主方程模拟,其中考虑了有限量子比特相干性和声子通道损耗。不确定性是相对于平均值的标准偏差。
利用超表面进行 Grover 量子搜索算法的表面声波计算
由于并行处理的优势,基于波的计算最近引起了广泛关注。特别是,已经证明了几种声波计算设备可以执行经典算法和数学运算。在这里,我们扩展了声波计算以模拟量子算法,提出了一种支持欺骗表面声波的集成声学梯度超表面系统来实现 Grover 量子搜索算法。我们表明,这种集成元设备可以实现设计的亚衍射和透射相位,可用于模拟量子算法中使用的操作,例如 Hadamard 变换和平均值的逆。数值模拟证明了该设备具有良好的搜索能力,包括比经典算法快一倍的速度和亚波长搜索精度。我们预计,我们的结果将启发片上集成元设备的替代设计方案,以实现更多受量子启发的声学模拟计算。
在体外评估癌细胞诱导的...
表面声波是局限于材料表面的机械波。这些波浪自然发生在地震期间,并且还经过设计用于微型设备,在传感和处理超高频率电信号中起着至关重要的作用。人造表面声波通常以数百MHz或更高的频率运行,波长在千分尺尺度上,并且表面位移的表面位移数百个皮仪 - 可与原子的大小相当。可以通过在压电材料上的互换能器的机电转换来进行这些波的激发。表面声波的损失可能很低,结合能够通过压电材料中的应变或电场将多个量子系统搭配到许多量子系统,最近已实现了量子声学领域的探索。在经典级别上,这种耦合都是可能的,其中大量相干的声子与量子系统相互作用,以及在量子级别,量子系统理想地耦合到单个声子。这不仅对量子物理学研究非常有意义,而且对于从量子传感到量子转导的应用,其中量子信号从一种类型的载体转换(例如光子)到另一个(例如声子)。在本文中,我们与GAAS上的表面声波一起工作,GAA既是压电材料,又是半导体。以这种方式,可以在托有Ingaas量子点的同一介质中生成表面声波,这些介质是光学活跃的量子系统。可以通过将声子限制在声腔中并将量子点放在光学微腔中以增强光学读数来增强表面声波和量子点之间的耦合。为此,我们在这里描述了一个包括声学腔和开放式光学微腔的平台,在不久的将来,该平台将用于使用Gigahertz表面声波和Ingaas Semicicductor量子点进行量子声学实验。由于多种损失机制,高铁表面声波腔的制造并不是微不足道的。由于系统的复杂性,有限的元素模拟是耗时的,并且不容易执行。因此,高铁表面声波腔的制造通常涉及基于迭代样品制造和表征的优化过程。在我们的情况下,我们通过电子束光刻和Al上的Al上的AL纳米表面声波杆纳米表面的声波杆。这些空腔在1 GHz下运行,并包含用于表面声波激发的插入式传感器。在第2章中,着重于表面声波腔的表征,我们建立了基于纤维的扫描光学干涉仪,用于测量GHz表面声波的位移的幅度和相位,以及在声学空腔中成像它们的空间分布。表面表面声波腔的表征通常是通过使用相同的用于波激发的相同二聚体换能器的全电测量进行的。我们通过成像表面声波腔中的横向模式我们发现此方法不完整,并且可能导致误导信息,尤其是关于腔体内声场的分布。
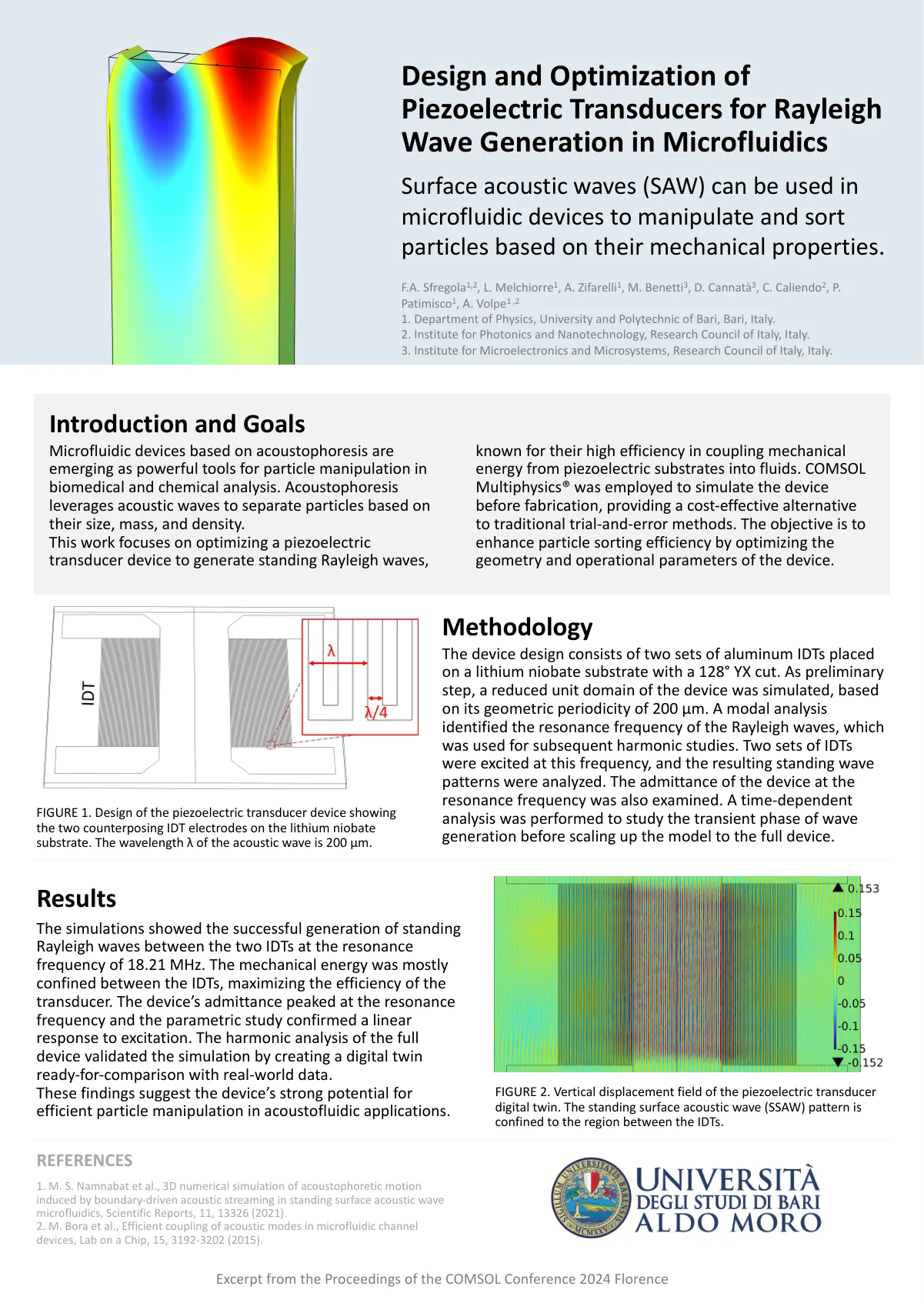
表面声波 (SAW) 可用于微流体装置,根据粒子的机械特性对其进行操纵和分类。
该器件设计由两组铝 IDT 组成,放置在具有 128° YX 切口的铌酸锂基板上。作为初步步骤,基于器件的几何周期 200 μm,模拟了器件的缩小单元域。模态分析确定了瑞利波的共振频率,该频率用于后续的谐波研究。两组 IDT 在该频率下受到激励,并分析了由此产生的驻波模式。还检查了器件在共振频率下的导纳。在将模型扩展到完整器件之前,进行了时间相关分析以研究波产生的瞬态阶段。
X 波段 epi-BAW 谐振器 - Debdeep Jena
滤波器是通信系统中的核心无源元件,随着 5G 技术、物联网、传感器和自动化的兴起,通信系统中的滤波器市场预计还会不断扩大。1 – 3 虽然表面声波 (SAW) 滤波器由于制造简单而在 2 GHz 以下占据主导地位,但它们在更高频率下的性能受到低表面声波速度、光刻复杂性和低品质因数的限制。1、4 与体声波 (BAW) 滤波器相比,窄叉指换能器 (IDT) 手指中的电迁移损伤和 SAW 的不均匀电流分布导致其功率处理能力较差。1 由于厚度延伸波的速度高于表面声波,因此 BAW 滤波器在 1.5 至 6 GHz 的较低 5G 频段占主导地位。高品质因数和高功率处理能力使 BAW 滤波器可以扩展到更高的频率,同时保持高 RF 性能。 1 由于这种电声滤波(因为声波的波长比相同频率的电磁波小得多)而带来的小型化优势,在毫米波范围(30 – 300 GHz)的较高频率下,其收益会逐渐减少。对于如此高的频率,使用基片集成波导 (SIW) 和腔体滤波器在光域中进行直接滤波占主导地位。5 – 9
真空沉积之前的UV/臭氧工艺
自1976年以来,石英晶体共振器领域的大多数制造商一直在使用UV/臭氧清洁。此过程中的一些原始工作是在该领域完成的。(请参见图5)超细石英底物对于制造非常稳定的频率控制装置所需的电极膜粘附至关重要。通常使用UV/臭氧是最终的清洁步骤,过程时间为1-5分钟。...表面声波(S.A.W.)设备也是具有相似制造过程和清洁要求的pi-ezoeleclectric设备。尼橙锂和石英用于制造锯设备。该行业组中的许多用户都使用连接角度仪或蒸汽成核测试来监视清洁度。
传感器
摘要:我们建议使用氮化铝 (AlN) 膜作为基于表面声波 (SAW) 的加速度测量的敏感元件。将所提出的解决方案与基于使用石英 (SiO 2 )/铌酸锂 (LiNbO 3 ) 膜的现有原型进行了比较,这些膜具有广泛的各向异性。使用 COMSOL Multiphysics 5.4 计算机模拟,我们明确表明基于各向异性较小的 AlN 膜的敏感元件克服了 SiO 2 的低灵敏度限制和 LiNbO 3 的低温稳定性。此外,与 SiO 2 相比,AlN 膜对不可逆机械变形的坚固性几乎提高了两倍,这反过来又使基于 LiNbO 3 的传感器的灵敏度提高了 1.5 倍。考虑到它们可接受的频率特性,我们认为 AlN 膜是敏感元件的良好候选者,尤其是对于高加速度测量。
超导电路的量子声学
过去 20 年,电路量子电动力学发展迅速,超导量子比特和谐振器用于从根本上控制和研究量子光与物质的相互作用。该领域的发展受到量子信息科学和实现量子计算的前景的强烈影响,但也为不同物理系统和研究领域的结合提供了机会。微波领域的超导电路由于具有强大的非线性和零点涨落,以及设计和制造的灵活性,为与其他量子系统接口提供了一个多功能平台。基于电路量子电动力学的混合量子系统可以通过利用各个组件的优势来实现新功能。本论文涵盖了将超导电路与表面声波 (SAW)(沿固体表面传播的机械波)耦合的实验。可以利用 GaAs 基板的压电特性来实现强耦合,我们的实验利用这一点来研究量子场与物质相互作用的现象。表面声波的一个关键特性是传播速度慢,通常比真空中的光慢五个数量级,并且波长短。这使得在巨型原子领域中,超导电路形式的人造原子比相互作用的 SAW 辐射的波长大,这种情况在其他系统中很难实现。本论文中描述的实验利用这些特性来展示机械模式的电磁感应透明性,以及人造巨原子与 SAW 场之间的非马尔可夫相互作用。当 SAW 场被限制在谐振腔中时,短波长允许多模光谱适合与频率梳相互作用。我们使用多模 SAW 谐振器通过双音光谱方法表征微观两级系统缺陷的集合。最后,我们介绍了一种混合超导-SAW 谐振器,并考虑了其在量子信息处理中的应用。使用该设备进行的实验证明了 SAW 模式的纠缠,并在设计用于连续变量量子计算的簇状态的道路上显示出有希望的结果。