XiaoMi-AI文件搜索系统
World File Search System角动量
幼儿园量子力学毕业生
高功率激光脉冲一直是科学研究的重要组成部分，自Chirped Pulse Amplifation（CPA）发明使他们的一代变得更加可行。它们对于从激光唤醒物理学的应用研究（例如激光唤醒场）到对激光 - 血压相互作用的更基本研究以及探测非线性真空量子动力学（QED）效应的更多基本研究至关重要。2因此，已经对这些高功率脉冲的时间和空间方案的表征进行了大量研究。光的轨道角动量（OAM）是量化的电磁辐射自由度，其特征是梁u的横向相反的方位相依赖性； /þ / e l h，其中uðq; /; zÞ是该函数，它表征了圆柱坐标中的横向图，而L是方位角模式数，它量化了模式的OAM。与更熟悉的旋转角动量（SAM）不同，该动量与光的圆极化状态有关，OAM是无限的，可以采用任何整数值。自艾伦（Allen）等人以来。首先是电磁波
用数学方法探索早期纵向动力学
我们系统地研究了流体动力学模拟中超子全局极化对碰撞系统初始纵向流速的敏感性。通过在将初始碰撞几何映射到宏观流体动力学场时明确施加局部能量动量守恒，我们研究了系统的轨道角动量 (OAM) 和流体涡度的演变。我们发现同时描述 Λ 超子的全局极化和介子定向流的斜率可以强烈限制流体动力学演化开始时纵向流的大小。我们利用 RHIC 光束能量扫描程序中的 STAR 测量结果提取了初始纵向流的大小和产生的 QGP 流体中轨道角动量分数作为碰撞能量的函数。我们发现在流体动力学演化开始时，中快速度流体中剩余约 100-200 ℏ OAM。我们进一步考察了不同的流体动力学梯度对Λ和¯ Λ自旋极化的影响。µ B /T的梯度可以改变Λ和¯ Λ极化之间的有序性。
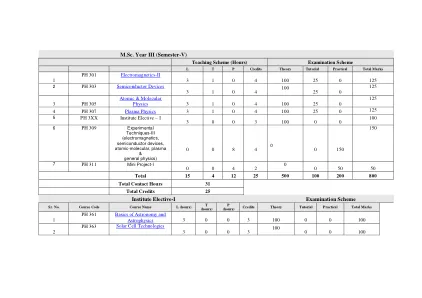
理学硕士第三年（第五学期）
教学大纲 电动力学 (08 小时) 电动势和运动电动势、法拉第电磁感应定律和磁场中的能量、麦克斯韦方程组、麦克斯韦如何固定安培定律、物质中的麦克斯韦方程组、边界条件 电动力学中的守恒定律 (06 小时) 连续性方程、坡印廷定理、电动力学中的牛顿第三定律、麦克斯韦应力张量、动量守恒定律、角动量 电磁波 (08 小时) 一维波、真空和物质中的电磁波、物质中的吸收和弥散、导波 势与场 (07 小时) 标量势和矢量势、规范变换、库仑规范和洛伦兹规范、延迟势、 Jefimenko 方程、Lienard-Wiechert 势、移动点电荷的场辐射（06 小时）电偶极子辐射和磁偶极子辐射、任意源的辐射、点电荷辐射的功率、辐射反应电动力学和相对论（07 小时）狭义相对论和相对论力学、相对论电动力学、场张量、张量符号中的电动力学。
水波中的场论自旋和动量
自旋是量子粒子或场的一个基本但非平凡的固有角动量属性，它出现在相对论场论中。波场中的自旋密度由基于正则动量密度和动能动量密度之间差异的理论 Belinfante-Rosenfeld 构造描述。这些量通常被认为是抽象的和不可观察的。在这里，我们从理论和实验上证明，Belinfante-Rosenfeld 构造自然出现在重力（水面）波中。在那里，正则动量与广义斯托克斯漂移现象有关，而自旋是由水粒子的亚波长圆周运动产生的。因此，我们直接将这些基本场论属性观察为经典波系统的微观力学属性。我们的发现揭示了波场中自旋和动量的性质，证明了相对论场论概念的普遍性，并为它们的研究提供了一个新的平台。
利用经典光学教授量子概念
令人惊讶的是，最近的研究表明，纠缠这种传统上被认为是量子独有的不可分离特征也可以存在于经典光场中 [1-10]。随着量子概念和经典光学之间的模拟分析越来越多，人们越来越关注经典光纠缠领域。经典光中的量子模拟概念已被证明能够违反贝尔不等式 [2]，改进偏振的测量和量化 [3,4]，控制基本的波粒二象性 [5,6]，模拟简单的量子任务 [7-9] 等。这些令人鼓舞的结果表明，经典纠缠光可以作为一个物理平台，用于教学基本的量子概念，甚至展示简单量子信息和计算任务的实现。这里我们提出利用经典光束的张量结构来引入矢量空间、叠加、角动量、相干性、纠缠、干涉、量子比特类似物、量子信息等量子概念。光束包含三个主要自由度 (DOF)，即偏振、空间特性和时间特性，一般可以描述为
湍流记忆对理想化龙卷风的影响......
摘要：表面摩擦通过增强角动量的收敛而促进龙卷风的形成和维持。大气模型中的传统下边界条件通常假设未解析应力和解析剪切之间存在瞬时平衡。该假设忽略了湍流运动以有限速率产生和消散的物理原理——实际上，湍流在其整个生命周期中都有记忆。在本文中，提出了一种改进的下边界条件来解释湍流记忆的影响。具体而言，当气团沿弯曲轨迹移动时，由于湍流记忆，会产生正常表面剪切应力分量。在理想龙卷风的大涡模拟 (LES) 中，正常表面剪切应力分量是额外动态不稳定性的一个来源，为湍流运动的发展提供了一条额外的途径。只要修改后的下边界条件所采用的假设在感兴趣的流动区域的较大部分内成立，湍流记忆对准稳态龙卷风强度的影响就可以忽略不计。然而，瞬态龙卷风可能对湍流记忆特别敏感。
旋转attosecond Electron和Ultra-Brilliant Multi ...
抽象隔离的多MEVγ射线，持续时间，高准直和梁角动量（BAM）可能会在核物理学，天体物理学等中找到许多有趣的应用。在这里，我们提出了一种方案，通过非线性汤姆森散射生成这种γ-射线，该旋转相对论电子板由几个周期扭曲的激光脉冲驱动，与微滴定目标相互作用。我们的模型清楚地确定了激光强度阈值和载体 - 内玻璃相对隔离电子纸的产生的影响。三维数值模拟表明，γ射线发射的持续时间为320次，峰值光彩为9.3×10 24光子S -1 mrad -2 mm -2 mrad -2 mm -2每0.1％带宽在4.3 MEV时。γ-射线梁的大BAM为2.8×10 16ℏ，这是由有效的BAM转移来自旋转电子板的有效BAM转移，随后导致了独特的角度分布。这项工作应促进对大型激光设施中旋转电子片的非线性汤姆森散射的实验研究。
Xygkou，Anna，Siriaraya，Panote，She，Wan Jou，Covaci，Alexandra和Siang Ang，Chee（2024）“我可以与聊天机器人更加社交吗？我们可以打破基于自旋的电子设备的界限吗？
摘要我们发现，与1 e = 2 µ b b表示读取或擦除自旋数据的最小能量应与1961年Landauer提出的1 E = K B T Ln（2）表示。使用旋转方向代表一些信息的物理学与在基于经典的基于电荷的数据存储中使用粒子的位置的物理学根本不同：前者是量子动力的（独立于居里点以下的温度），而后者是热力学（依赖温度）。定量，与新信息擦除协议相关的这种新能量估计为1。64×10 - 36 J，比Landauer结合（3×10 - 21 J）低15个数量级，无需成本的角动量和总熵增加。在此新信息擦除协议中，无需将电子从电位的一侧移至另一侧，否则用于保留定义旋转状态的能量仍然需要大于现有的热闪光（Landauer Bound）。我们根据包括Rydberg Atom和Spin-Spin相互作用在内的许多实验来验证我们的新能量结合。
在A2MGREO6中的自旋轨道固定状态（a = ca，sr ...
虹膜物理学，近年来其他5 d过渡金属（TM）离子系统引起了人们的兴趣，包括5 d 1订购的双钙钛矿（DP）系统，用于其建议托管“隐藏”多极阶（5 D1¼W5Þ，re6Þ，re6Þ，os 7 s）[1-13] [1-13]。至关重要的是，典型的原子图有效地理解了液体物理学并不能令人满意地解释5 d 1 dps的物理学。在公式A 2 bb 0 O 6的5 d 1 dps中，唯一磁性5 d 1离子占据B 0位点，并具有由J effeff¼3= 2所描述的四倍退化基态构型。以这样的配置，随着角动量的自旋和轨道成分消失的净磁矩m¼2s-l消失了[1]。基于原子图的消失磁矩的预测失败了，但是，对于具有有限的磁矩的真实材料的情况[3,8,10]。存在被抑制但非零的杂志偶极矩的存在通常归因于空间扩展的TM-5 d轨道与