XiaoMi-AI文件搜索系统
World File Search System拓扑层结构中的光学双稳态及其在光神经网络中的应用*
材料Sio 2。在拓扑模式下,电场高度局部位于分层结构的反转中心(也称为界面),并成倍地衰减到批量上。因此,当从战略上引入非线性介电常数时,出现了非线性现象,例如Biscable状态。有限元数值模拟表明,当层周期为5时,最佳双态状态出现,阈值左右左右。受益于拓扑特征,当将随机扰动引入层厚度和折射率时,这种双重状态仍然存在。最后,我们将双态状态应用于光子神经网络。双态函数在各种学习任务中显示出类似于经典激活函数relu和Sigmoid的预测精度。这些结果提供了一种新的方法,可以将拓扑分层结构从拓扑分层结构中插入光子神经网络中。
人工智能在油气钻井工程中的应用
进入石油和天然气钻井工程,改善了钻井操作的智能水平。根据国内外石油和天然气钻探工程的当前研究状况,本文讨论了人工智能在石油和天然气钻探工程中的关键技术应用。智能钻井和完成技术结合了大数据,人工智能算法和软件平台,以优化关键技术,例如井眼轨迹,定向钻孔和钻孔速度,以提高操作安全性和效率。其次,智能钻井设备的研发和应用在国际上是相对成熟的。诸如智能钻机,钻头和旋转转向系统之类的设备已经达到了高度的自动化,从而提高了运行效率并降低了人工成本。最后,钻井和完成软件系统通过引入机器学习和云计算等技术来集成和分析大量数据,从而优化了钻孔设计和操作。尽管中国在智能钻探软件和设备领域开始后期开始,但它取得了一些进展,主要是在监视优化和设计方面。将来,随着核心技术的突破,人工智能将为石油和天然气资源的发展带来一场技术革命。中国需要继续加强基础研究,结合行业的实际需求,并促进独立的技术创新和应用促进,以提高智力的整体水平,并通过国际高级技术来缩小差距。
2014 CSR - 中华航空
华航成立于1959年,即将迈入第56个年头。「留住满意的顾客与快乐的员工,为股东与社会创造最大价值」一直是华航自成立以来的经营理念。华航致力成为最值得信赖的世界级航空公司,以最佳的飞行品质,让每一位旅客都感到满意。截至2015年6月30日,华航客货机队规模已扩展至86架,航线网络覆盖全球29个国家115个航点。去年,在大家的共同努力下,华航及其关联企业交出亮眼的成绩单。2015年,受国际油价平稳、日圆贬值、大陆旅客经台过境限制即将解除等因素影响,旅客量持续增长,货运市场也逐渐回暖。感谢每一位华航员工、旅客、股东及伙伴的支持与鼓励。
糖尿病与卒中后抑郁的研究进展
中风后抑郁症是中风的常见并发症,严重影响了患者的生活和生活质量。大约三分之一的中风患者被诊断出患有糖尿病,糖尿病会加剧卒中后抑郁症的风险。在病理生理学方面,两者之间存在相互加强的关系。本文将探讨糖尿病与中风后抑郁症之间的病理生理联系,并从药物疗法的角度进行分析,旨在为也患有糖尿病的卒中后抑郁症患者提供预防和治疗参考。
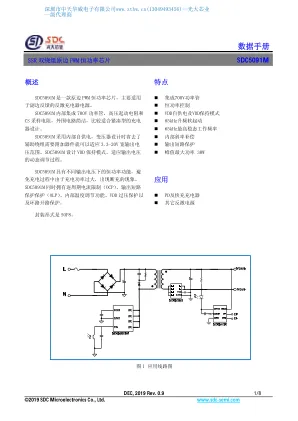
数据手册 - 中天华威
2019年12月Rev.0.9 1/8©2019 SDC Microelectronics Co.,Ltd。www.sdc-semi.com0.9 1/8©2019 SDC Microelectronics Co.,Ltd。www.sdc-semi.com
中华民国血液病学会中华民国血液及骨髓移植...
M.D.(H.K.)2020年遗传学和基因组学研究员(医学)(HKCP)2023先前的职位:香港皇后医院内部官员(2006年7月1日至2007年6月30日)。 香港皇后医院医学系医学官(2007年7月1日至2014年6月30日)。 香港大学医学系临床助理教授(2014年7月1日至2023年6月30日)。 现任职位:香港皇后医院医学系荣誉副顾问(2020年7月1日 - 现在)香港格兰瑟姆医院姑息医疗部门的荣誉副顾问(2020年7月1日 - 目前)。 香港大学医院(2023年3月1日至至至12月1日)医学系荣誉副顾问,香港大学医学系临床副教授(2023年7月1日 - 目前)先前的相关研究工作:1。 骨髓增生综合征(MDS)和急性髓样的临床和基因组注册表2020年遗传学和基因组学研究员(医学)(HKCP)2023先前的职位:香港皇后医院内部官员(2006年7月1日至2007年6月30日)。香港皇后医院医学系医学官(2007年7月1日至2014年6月30日)。 香港大学医学系临床助理教授(2014年7月1日至2023年6月30日)。 现任职位:香港皇后医院医学系荣誉副顾问(2020年7月1日 - 现在)香港格兰瑟姆医院姑息医疗部门的荣誉副顾问(2020年7月1日 - 目前)。 香港大学医院(2023年3月1日至至至12月1日)医学系荣誉副顾问,香港大学医学系临床副教授(2023年7月1日 - 目前)先前的相关研究工作:1。 骨髓增生综合征(MDS)和急性髓样的临床和基因组注册表香港皇后医院医学系医学官(2007年7月1日至2014年6月30日)。香港大学医学系临床助理教授(2014年7月1日至2023年6月30日)。现任职位:香港皇后医院医学系荣誉副顾问(2020年7月1日 - 现在)香港格兰瑟姆医院姑息医疗部门的荣誉副顾问(2020年7月1日 - 目前)。香港大学医院(2023年3月1日至至至12月1日)医学系荣誉副顾问,香港大学医学系临床副教授(2023年7月1日 - 目前)先前的相关研究工作:1。 骨髓增生综合征(MDS)和急性髓样的临床和基因组注册表香港大学医院(2023年3月1日至至至12月1日)医学系荣誉副顾问,香港大学医学系临床副教授(2023年7月1日 - 目前)先前的相关研究工作:1。骨髓增生综合征(MDS)和急性髓样的临床和基因组注册表
食物中毒细菌在低温下在食物中生长
近 10 年国外重大李斯特菌疫情 国家 疫情年份 致病食物 患者人数 死亡人数 澳大利亚 2013 奶酪 18 2 丹麦 2013-2014 熟食肉类 41 17 美国 2014 豆芽 5 2 美国、加拿大 2014-2015 焦糖苹果 36 7 美国 2010-2015 冰淇淋 10 3 美国 2015 软奶酪 24 1 美国、加拿大 2015-2016 包装沙拉 47 1 美国 2013-2016 冷冻蔬菜 9 1 德国 2012-2016 疑似来自同一工厂的多种产品 66 3 澳大利亚 2018 甜瓜 20 7 南非 2017-2018 肉制品 1,060 216 丹麦、德国、法国2015-2018 熏制三文鱼 7 1 奥地利、丹麦、芬兰等 2015-2018 冷冻玉米 47 9 丹麦、爱沙尼亚、芬兰等 2014-2019 冷熏鱼制品 22 5 英国 2019 三明治和沙拉 9 6 西班牙 2019 熟肉制品 207 例确诊,3059 例高度疑似 3 美国、加拿大 2017-2019 熟鸡丁 31 2 荷兰、比利时 2017-2019 肉制品 21 3 美国、澳大利亚 2016-2019 金针菇 42 5 美国 2017-2019 煮鸡蛋 8 1 美国 2020-2020 熟食肉类 11 1 美国 2014-2022 预包装沙拉 18 3 英国2020-2022 熏鱼 12? 美国 2021-2022 冰淇淋 25 1 美国 2021-2022 熟食肉 14 1 美国 2023 奶昔 6 3 美国 2018-2023 绿叶蔬菜 19 0 瑞士 2022 熏鱼 20 ? 美国 2018-2023 桃子、油桃、李子 11 1 德国、荷兰、比利时、英国等 2012-2024 鱼制品 73 14 加拿大 2023-2024 冷藏杏仁奶等 20 3 美国 2024 熟食肉类 59 10 10
卒中后抑郁发病机制的研究进展
中风后抑郁症(PSD)是中风患者的常见神经和心理障碍,其特征是情绪和兴趣下降,可以降低患者在治疗过程中的能力,主动性和积极性。PSD可能导致康复结果不佳,影响日常生活,甚至在严重的情况下甚至危害生命。尽管我们对PSD的不良反应有了更深入的了解,但其确切的发病机理仍不清楚,并且进一步进一步 -
“最近发展区”理论在教学中的应用分析
“最近发展区”理论、DNA 作为主要遗传物质、学习支架、教学效率版权所有 © 2025 作者和 Hans Publishers Inc. 本作品根据知识共享署名国际许可证 (CC BY 4.0) 获得许可。http://creativecommons.org/licenses/by/4.0/
高阳科技(中国)有限公司
鉴于2023年国内市场利率持续偏低,穗信云链把握机遇,加强与各大金融机构的紧密合作,以更高效率、更低利率为中小企业提供信贷支持。集团不仅全面支持新一代票据及供应链票据受理,还加强银行承兑汇票受理,与近10家银行合作。随着穗信云链服务受理能力的进一步提升,2023年交易规模突破百亿元,较去年同比增长131%。其中票据业务同比增长185%,带动金融科技服务板块经营利润达4,300万港元,同比增长190%。