机构名称：
¥ 1.0
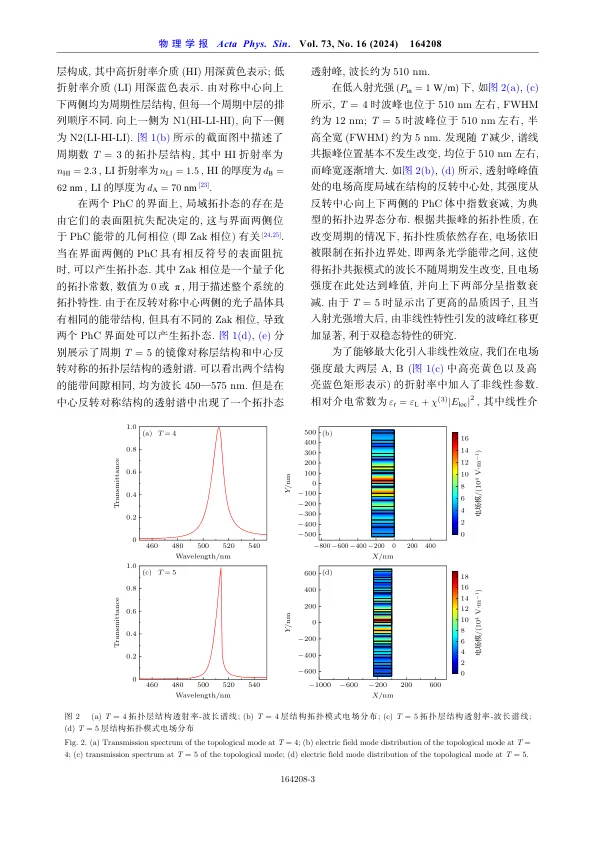
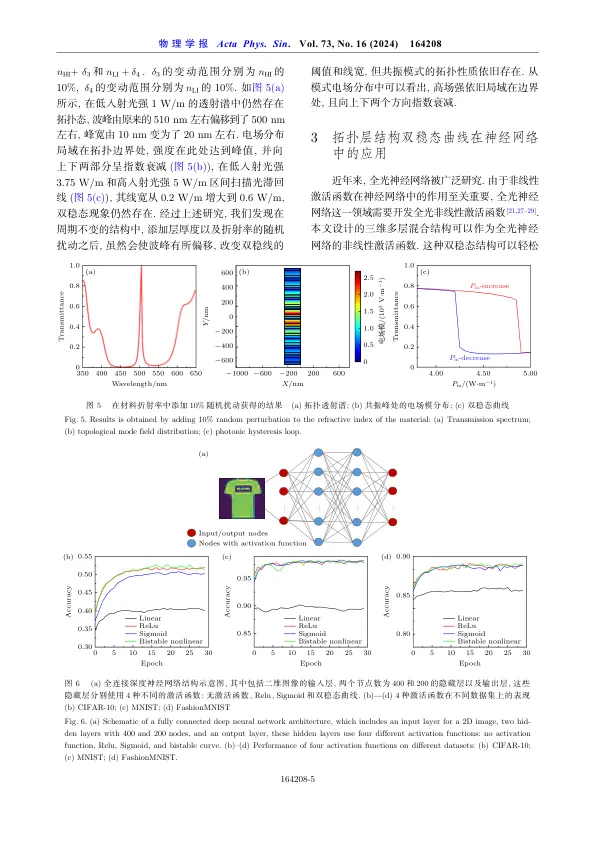
材料Sio 2。在拓扑模式下，电场高度局部位于分层结构的反转中心（也称为界面），并成倍地衰减到批量上。因此，当从战略上引入非线性介电常数时，出现了非线性现象，例如Biscable状态。有限元数值模拟表明，当层周期为5时，最佳双态状态出现，阈值左右左右。受益于拓扑特征，当将随机扰动引入层厚度和折射率时，这种双重状态仍然存在。最后，我们将双态状态应用于光子神经网络。双态函数在各种学习任务中显示出类似于经典激活函数relu和Sigmoid的预测精度。这些结果提供了一种新的方法，可以将拓扑分层结构从拓扑分层结构中插入光子神经网络中。
拓扑层结构中的光学双稳态及其在光神经网络中的应用*
主要关键词
相关文件推荐
