XiaoMi-AI文件搜索系统
World File Search System氧化镍超导体在高温下超高...
在第二年,铜氧化物 *2中高温超导性的发现是极快的杰作,并且是一部杰作,它将留在科学史上。自2000年代初以来,Kuroki教授及其小组一直在研究实现TC的策略,该策略超过了氧化铜。尽管可以在理论模型的范围内实现高T C,但使用真实材料实现这一点并不容易。经过各种考虑,黑子教授和其他人在2017年的论文A中发现,即使不是理想的理论模型本身,La 3 Ni 2 O 7也可以达到类似的情况。六年后的2023年5月,来自中国中央大学的一个小组在其预印式服务器Arxiv上宣布,La 3 Ni 2 O 7在压力下以T C = 80K的最大t c = 80K表现出高温超导性,并于9月在自然界发表(H. Sun等人,自然,自然621,493(20233))。自从本文出现在5月的Arxiv上以来,Kuroki教授,Sakakibara副教授和Ochi副教授已经开始了联合研究,并于6月发表了有关Arxiv的论文。从那时起,关于ARXIV的大量相关实验和理论论文已经发表,并且在全球范围内一直在蓬勃发展。
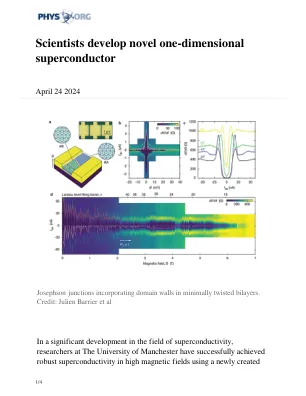
科学家发展了新颖的一维超导体
这项研究本周(2024年4月25日)在本质上发表,详细介绍了由安德烈·吉姆(Andre Geim)教授,朱利安·巴里埃(Julien Barrier)博士和纳Xin博士领导的曼彻斯特团队的广泛工作,以在量子厅政权中实现超导性。他们的最初努力遵循传统的途径,在传统途径中,反向传播的边缘彼此靠近。但是,这种方法被证明是有限的。
通过拓扑超导体接触的量子点的瞬态效应
我们研究了两个量子点的逐渐发展,这些量子点附着在拓扑超导纳米线的相对侧,托有边界模式。特别是,我们探索通过零能量的主要模式在这些量子点之间传递的非平衡互相关。我们的分析和数值结果揭示了电子配对的瞬态行为中可观察到的非本地特征,随后杂交结构朝着其渐近稳态构造进化。我们估计这些暂时现象的持续时间。使用时间依赖性数值重新归一化组技术的非扰动方案,我们还分析了与接近度诱导的电子配对竞争的相关效应的非平衡特征。这些动力学过程可以使用超导杂交纳米结构对拓扑和 /或常规的超导量子位施加的编织方案表现出来。
平面超导体中的相关函数和特征长度
在平面频带(FB)材料中,高温超导性非常规形式的可能性并不能挑战我们对相关系统中物理学的理解。在这里,我们计算了在各个一维FB系统中的正常和异常的单粒子相关函数,并系统地提取特征长度。当Fermi能量位于FB中时,发现相干长度(ξ)是晶格间距的顺序,并且对电子电子相互作用的强度较弱。最近,有人认为,在FB化合物中可以将ξ分解为BCS类型的常规部分(ξBCS),而几何贡献则表征了FB本征态,量子度量()。但是,通过以两种可能的方式计算连贯长度,我们的计算表明ξ̸= p
1拓扑kagome磁铁和超导体jia- ...
一个kagome晶格自然具有其电子结构中的Dirac Fermions,Flat Band和Van Hove奇异性。Dirac Fermions编码拓扑结构,平面带偏爱相关现象,例如磁性,而Van Hove的奇异性可以导致对远程多个体型的不稳定性,从而完全可以实现和发现一系列拓扑kagome磁铁,并具有带有exotic特性的超导体。探索kagome材料的最新进展揭示了由于几何,拓扑,自旋和相关性之间的量子相互作用而产生的丰富的新兴现象。在这里,我们回顾了该领域的这些关键发展,从Kagome晶格的基本概念开始,再到Chern和Weyl拓扑磁性的实现,再到各种平坦的多体型相关性,然后再到非常规的电荷密度密度波和超导导性的难题。我们强调了理论思想和实验观察之间的联系,以及kagome磁铁和kagome超导体内的量子相互作用之间的键,以及它们与拓扑绝缘子,拓扑超导体,Weyl Semimetals和高磁性超管制的概念之间的关系。这些发展广泛地桥接了拓扑量子物理学,并将多体物理物质相关联,并在各种散装材料中与拓扑量子问题的前沿相关。
与不同配对的Weyl超导体的对称性
我们检查了Bogoliubov-de Gennes Hamiltonian及其对称性对称性,用于分时交换对称性破碎的三维Weyl超导体。在消失的配对电位的极限中,我们指定该哈密顿量在两组持续对称性下是不变的,即u(1)量规对称性和u(1)轴向对称性。尽管Bardeen-Cooper-Schrie Q er类型的配对会自发打破这两个对称性,但我们表明,Fulde-Ferrell-Larkin-ovchinnikov型配对的fulde-ferrell-ferrell-ferrell-larkin-ovchinnikov型配对会自发地破坏u(1)的对称性(然后通过众所周知的超级量表模式恢复了超级质量验证模式)。因此,在前一种情况下,系统中需要两种NAMBU-GOLDSTONE模式来恢复损坏的对称性。我们表明这两种模式之一是出现的伪标量相模式。我们还证明了这种相位模式会导致伪 - 甲壳虫效应。
为量子计算机构建拓扑超导体
尽管量子计算机提供了无数机会,但它们的实际应用迄今为止仍因其易受周围环境影响而受到阻碍。印第安纳州圣母大学的 Badih Assaf 博士、Xinyu Liu 博士及其同事展示了如何通过使用一种名为“拓扑超导体”的奇异杂化材料来克服这些问题。通过优化这些材料的制造并详细分析其量子特性,该团队的研究结果可以为拓扑超导体在坚固实用的量子计算机中的广泛应用铺平道路。
Alp Sipahigil - 超导体光学互连
摘要:存储、传输和处理量子信息的能力有望改变我们计算、通信和测量的方式。在过去的二十年里,基于约瑟夫森结的超导微波电路成为量子计算的强大平台。然而,这些系统在低温和微波频率下运行,需要相干光互连才能长距离传输量子信息。在这次演讲中,我将介绍我们最近的实验,展示超导量子比特激发到光子的转换。我将介绍一个集成设备平台,该平台结合了超导量子比特、压电换能器和光机械换能器,用于在超导电路、单个声子和单个光子之间转换量子态。我将讨论如何使用处于量子基态的纳米机械振荡器将单个光子从微波频率转换为光学域。最后,我将讨论这种方法在实现基于超导量子处理器的未来量子通信网络方面的前景。
配对对称性对镍超导体LA3NI2O7
在压力下,在LA 3 Ni 2 O 7中发现了高温超导性。然而,从理论上讲,对其配对对称性尚未达成共识。通过将密度函数理论(DFT)结合,最大定位的频函数和线性差距方程与随机相位及相关性,我们发现,如果La 3 Ni 2 O 7的配对对称性为D XY,则如果其DFT频带的结构准确地由下flowdolded byborbiane twopord twopold twopord twopord twoce xy。更重要的是,我们揭示了La 3 Ni 2 O 7的配对对称性敏感地取决于两个Ni-e G轨道之间的晶体场分裂。ni-e g晶体场的略有增加分裂改变了配对对称性从d xy到s±。这种转变与费米速度和敏感性的变化有关,而费米表面的形状几乎保持不变。我们的工作强调了多轨超导体中低能电子结构对对称性的敏感依赖性,当一个人计算其配对对称性时,它在下垂过程中需要注意。
生物系统作为超导体:第一部分内容
2一般TGD关于超导性的观点10 2.1超导性的基本现象学。。。。。。。。。。。。。。。。。。。。。10 2.1.1超导性的基本现象学。。。。。。。。。。。。。。。。。。10 2.1.2普遍性超级导体的基本参数?。。。。。。。。。。。10 2.2 TGD框架中参数的通用性。。。。。。。。。。。。。。。。。12 2.2.1 P-ADIC缩放对超导体参数的影响。。。。。13 2.3量子关键性和超导性。。。。。。。。。。。。。。。。。。。。。14 2.3.1超导体的量子临界与TGD量子临界有之间的关系。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 2.3.2扩大量子重叠的de broglie波长和标准。。15 2.3.3 TGD框架中的量子临界超导体。。。。。。。。。。。。15 2.3.4量子关键性可以使新型高T C超导体可能成为可能吗?16 2.4时空描述苏斯传统的机制。。。。。。。。。17 2.4.1主要问题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 2.4.2光子量,库珀对的相干状态和虫洞接触18 2.4.3时空相关,以量子关键超导性。。。。。。。。。19 2.5在磁通管处的超导性。。。。。。。。。。。。。。。。。。。。。19 2.5.1地球磁场的量子的超导体。。。。。。20 2.5.2超导磁性磁管和壁的能量差距。。。。。。。20