XiaoMi-AI文件搜索系统
World File Search System本科学位课程 B 的教学大纲......
1 描述统计:a) 集中趋势测量 - 分组和非分组数据;平均值、样本平均值 - 加权平均值;中位数、四分位数、b) 十分位数和百分位数、箱线图、众数变异测量 - 离差、范围、标准差、总体与样本方差和标准差、偏度、峰度。2 概率和抽样分布简介:a) 分配概率的方法、概率空间、概率模型的条件、事件、简单和复合、概率定律、概率密度函数、累积分布函数、平均值和方差的预期值。边际、联合、联合和条件概率,贝叶斯定理 b) 随机变量、离散和连续分布、期望、分布矩、二项分布、泊松分布、均匀分布和正态分布、二项分布的正态近似、多个随机变量的分布、联合分布矩、独立性、协方差、相关系数、中心极限定理。3 假设检验:a) 总体参数的大样本估计和假设检验:估计总体均值和差异的基础知识;估计比例和差异;总体均值、差异的大样本检验;比例、差异的大样本检验。b) 总体方差的估计:方差的抽样分布,
B. Tech。土木工程计划
线性代数基础知识:向量空间和子空间,基础和维度,血统转换,四个基本子空间。矩阵理论:规范和空间,特征值和特征向量,特殊矩阵及其特性,最小平方和最小规范的解决方案。矩阵分解算法-SVD:属性和应用,低等级近似值,革兰氏施密特过程,极性分解。尺寸还原算法和JCF:主成分分析,血统判别分析,最小多项式和约旦的规范形式。微积分:微积分的基本概念:部分导数,梯度,定向衍生物Jacobian,Hessian,凸集,凸功能及其属性。优化:无约束和受约束的优化,受约束和不受约束优化的数值优化技术:牛顿的方法,最陡的下降方法,惩罚函数方法。概率:概率的基本概念:条件概率,贝叶斯定理独立性,总概率,期望和方差定理,几乎没有离散和连续分布,联合分布和协方差。支持向量机:SVM简介,错误最大程度地减少LPP,双重性和软边距分类器的概念。参考书:
图像和视频柔和对比度自我监督学习的相似性估计
抽象的对比表示学习已被证明是图像和视频的有效自我监督的学习方法。最成功的方法是基于噪声对比估计(NCE),并将实例的不同视图用作阳性,应与其他称为否定的实例形成对比,被称为噪声。但是,数据集中的几个实例是从相同的分布中汲取的,并共享基本的语义信息。良好的数据表示应包含实例之间的关系,语义相似性和差异性,即通过将所有负面因素视为噪声来损害对比学习。为了避免此问题,我们提出了一种新的对比度学习的表述,使用称为“相似性对比估计(SCE)”的实例之间的语义相似性。我们的训练目标是一个软的对比目标,它使阳性更接近,并估计根据其学到的相似性推动或提取负面实例的连续分布。我们在图像和视频表示学习方面均通过经验验证我们的方法。我们表明,SCE在ImageNet线性评估方案上的最低时期时代的较少时代的时期与最低的时期进行了竞争性,并且它概括为几个下游图像任务。我们还表明,SCE达到了预处理视频表示的最新结果,并且学习的表示形式可以推广到下游任务。源代码可用:https://github.com/juliendenize/eztorch。
1个基本属性和带结构
杂交轨道,通过混合2 s,2 p x和2 p y轨道形成三个SP 2杂交轨道,而第四轨道则保持为2 p z。重叠的SP 2杂交轨道来自两个相邻原子会产生强σ共价键(C - C键);这些平面σ键将每个碳原子连接到三个邻居。这些碳原子的其余2个P Z轨道形成π键,这些碳构成了将碳层结合在一起的石墨中。因为π键比σ键弱得多,所以石墨具有低剪切强度,因此可以轻松将其碳层脱离。对于单层石墨烯而言,这些几乎游离的π电子负责其大多数实验观察到的电子和光学特性。由于保利排除原理要求来自不同碳原子的π电子不占据相同的状态,因此石墨烯中大量紧密堆积的碳原子会导致退化的能量水平分裂为连续分布的非等级允许能量状态,从而形成能带。石墨烯的真实空间二维蜂窝晶格如图1.1(a)所示。石墨烯中两个相邻的碳原子之间的距离为
小鼠的前室深度受到几个定量性状基因座的控制
前室深度(ACD)是与一角闭合青光眼(PACG)相关的定量性状。尽管ACD高度可遗传,但已知的遗传变异解释了表型变异性的一小部分。这项研究的目的是使用小鼠菌株鉴定附加的ACD影响基因座。由86 N2和111 F2小鼠组成的队列是由重组近近近近近近将BXD24/ TYJ和野生衍生的铸造/ EIJ小鼠之间的十字产生的。使用前腔室光学相干断层扫描,在10-12周龄时表现出小鼠,基于93个全基因组SNP进行基因分型,并进行定量性状基因座(QTL)分析。在对所有小鼠的ACD分析中,六个基因座通过了p = 0.05的显着性阈值,并在多次回归分析后持续存在。这些是在染色体6、7、11、12、15和17上(分别为ACDQ6,ACDQ7,ACDQ11,ACDQ12,ACDQ15,ACDQ15和ACDQ17)。我们的发现证明了在小鼠中ACD遗传的定量多生成术,并确定了六个先前未识别的ACD影响基因座。我们采用了一种独特的方法来研究前室深度表型,通过使用小鼠作为遗传工具来检查这种连续分布的性状。
量子力学:保持真实吗?
众所周知,埃尔温·薛定谔在发现量子理论时,曾想将量子波函数ψ解释为表示电荷在三维空间中传播的连续分布。但人们不太了解的是,薛定谔最初也希望他的波函数用实值函数而不是复值函数来表示。在关于量子理论的一些早期论文以及写给亨德里克·洛伦兹和马克斯·普朗克的信中,薛定谔描述了他寻找实值波动方程的进展和挣扎,尽管他知道以他的名字命名的复值方程。最终,他发现了一个完全实的方程,等同于薛定谔方程,并将其称为“标量场ψ的均匀和一般波动方程”(2020,163)。在普朗克看来,他把这一突破描述为“闻所未闻的简单和闻所未闻的美”(Przibram 1967,16)。本文是探索这种形式的薛定谔方程的一种广告。假设我们将这个实方程视为量子理论的另一种表述,比如海森堡表述,甚至视为提供一种不同的本体论,将波函数的实部与 JS Bell 2004 所称的可视对象联系起来。我们是否会以不同的方式看待一些未解决的问题,又会出现什么新问题?在概述历史和一些背景之后,我将说明如何使用这种替代形式来理解量子基础中的问题。受 Struyve 2020 的最新论文的启发,我将展示“实薛定谔方程”如何极大地改变量子理论中关于时间反转不变性的难题。我希望读者能找到其他类似的例子,其中“保持真实”可以有所帮助。
机械工程教学大纲(MTQP07)
单元1:工程数学线性代数:矩阵代数,线性方程系统,特征值,特征向量。Calculus: Mean value theorems, Theorems of integral calculus, Evaluation of definite and improper integrals, Partial Derivatives, Maxima and minima, Multiple integrals, Fourier series, Vector identities, Directional derivatives, Line integral, Surface integral, Volume integral, Stokes's theorem, Gauss's theorem, Divergence theorem, Green's theorem.微分方程:一阶方程(线性和非线性),具有恒定系数的高阶线性微分方程,参数变化的方法,Cauchy方程,Euler方程,初始值和边界值问题,部分微分方程,部分微分方程,变量分离方法。复杂变量:分析函数,Cauchy的积分定理,Cauchy的积分公式,Taylor系列,Laurent系列,残基定理,解决方案积分。概率和统计:对定理,有条件的概率,平均值,中位数,模式,标准偏差,随机变量,离散和连续分布,Poisson分布,正态分布,二项式分布,相关分析,回归分析分析,回归分析分析:矩阵逆上的矩阵倒立,求解非元素平等的方法,差异和差异化方法,差异和差异化方法,差异和差异性方法差异化方法,差异差异和差异化方法差异化方法和差异方法。相关分析。单元2:应用力学和设计工程机制:自由图和平衡;摩擦及其应用,包括滚动摩擦,Belt-Pulley,刹车,离合器,螺丝千斤顶,楔子,车辆等。;桁架和框架;虚拟工作;平面运动中刚体的运动学和动力学;冲动和动量(线性和角度)以及能量配方;拉格朗日方程。材料力学:应力和应变,弹性常数,泊松比; Mohr的圆圈,用于平面应力和平面应变;薄缸; shear force and bending moment diagrams;弯曲和剪切应力;剪切中心的概念;梁的挠度;圆形轴的扭转;欧拉的
电气,功率和能源工程(MTQP10)。 ...
电气,功率和能源工程(MTQP10)单元1:工程数学线性代数:矩阵代数,线性方程系统,特征值,特征向量。Calculus: Mean value theorems, Theorems of integral calculus, Evaluation of definite and improper integrals, Partial Derivatives, Maxima and minima, Multiple integrals, Fourier series, Vector identities, Directional derivatives, Line integral, Surface integral, Volume integral, Stokes's theorem, Gauss's theorem, Divergence theorem, Green's theorem.微分方程:一阶方程(线性和非线性),具有恒定系数的高阶线性微分方程,参数变化的方法,Cauchy方程,Euler方程,初始值和边界值问题,部分微分方程,部分微分方程,变量分离方法。复杂变量:分析函数,Cauchy的积分定理,Cauchy的积分公式,Taylor系列,Laurent系列,残基定理,解决方案积分。概率和统计:对定理,有条件的概率,平均值,中位数,模式,标准偏差,随机变量,离散和连续分布,Poisson分布,正态分布,二项式分布,相关分析,回归分析分析,回归分析分析:矩阵逆上的矩阵倒立,求解非元素平等的方法,差异和差异化方法,差异和差异化方法,差异和差异性方法差异化方法,差异差异和差异化方法差异化方法和差异方法。相关分析。桥梁:惠特斯通,开尔文,梅戈赫姆,麦克斯韦,安德森,Schering和Wien,用于测量R,L,C和频率,Q-meter。4-20 MA两线发射器。单元2:仪器,控制和自动化测量和仪器:SI单元,标准(R,L,C,电压,电流和频率),测量表达的系统和随机误差,不确定性的表达 - 准确性和精度,误差,线性和加权回归的传播。单相电路中电压,电流和功率的测量; AC和DC电流探针;真正的RMS仪表,电压和电流尺度,仪器变压器,计时器/计数器,时间,相位和频率测量,数字电压计,数字万用表;示波器,屏蔽和接地。电阻,电容,电感,压电,霍尔效应传感器和相关的信号调节电路; transducers for industrial instrumentation: displacement (linear and angular), velocity, acceleration, force, torque, vibration, shock, pressure (including low pressure), flow (variable head, variable area, electromagnetic, ultrasonic, turbine and open channel flow meters) temperature (thermocouple, bolometer, RTD (3/4 wire), thermistor, pyrometer and semiconductor);液位,pH,电导率和粘度测量。
SCM关键概念中的MITX MicroMasters程序
1供应链分析3 1.1供应链管理概述。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4 1.1.1摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4 1.1.2关键概念。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4 1.2数学函数。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 1.2.1摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 1.2.2关键概念。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 1.3数据管理。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10 1.4概率。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11 1.4.1摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11 1.4.2关键概念。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11 1.4.3离散分布。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14 1.4.4连续分布。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 1.5统计。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。19 1.5.1统计测试和中心极限定理。。。。。。。。。。。。。。。。。。。。19 1.5.2抽样和置信间隔。。。。。。。。。。。。。。。。。。。。。。。。。。。19 1.5.3假设检验。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。23 1.5.4多个随机变量。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。25 1.6回归。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。26 1.6.1摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。26 1.6.2普通最小二乘线性回归。。。。。。。。。。。。。。。。。。。。。。。26 1.7优化。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。29 1.7.1摘要。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。29 1.7.2关键概念。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。30 1.7.3受约束优化。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。31 1.7.4线性程序。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。31 1.7.5整数和混合整数程序。。。。。。。。。。。。。。。。。。。。。。。。33 1.8网络和非线性编程。。。。。。。。。。。。。。。。。。。。。。。。。。。。38 1.8.1网络模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。38 1.8.2非线性优化。。。。。。。。。。。。。。。。。。。。。。。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>40 1.9算法和近似值。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>41 1.9.1摘要。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>41 1.9.2算法。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。。。。。。。。41 1.9.3最短路径问题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。42 1.9.4 Dijkstra的算法。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。43 1.9.5旅行推销员问题(TSP)。。。。。。。。。。。。。。。。。。。。。。。。。。。43 1.9.6车辆路由问题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。44 1.9.7 Clark-Wright Savings算法。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 45 1.9.8节省启发式。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 46 1.9.9用MILP解决VRP。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。44 1.9.7 Clark-Wright Savings算法。。。。。。。。。。。。。。。。。。。。。。。。。。。。45 1.9.8节省启发式。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。46 1.9.9用MILP解决VRP。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。46 1.9.9用MILP解决VRP。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。46
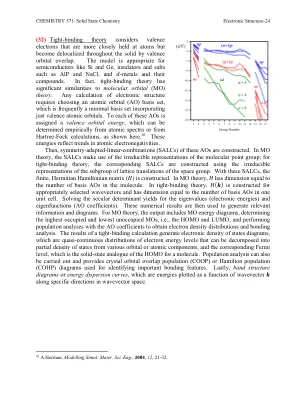
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道重叠进行了离域。该模型适用于SI和GE等半导体,ALP和NACL等绝缘体和盐,以及𝑑金属及其化合物。实际上,紧密结合理论与分子轨道(MO)理论具有显着相似之处。电子结构的任何计算都需要选择原子轨道(AO)基集,该集通常是最小的基础集,仅包含价原子轨道。对这些AOS中的每一个都分配了价值轨道能,可以从原子光谱或Hartree-fock计算中进行经验确定,如下所示。10这些能量反映了原子电负性的趋势。然后,构建了这些AOS的对称适应性线性组合(SALC)。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。 使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。 在MO理论中,𝐻具有等于分子中基本AO的数量。 在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。 求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。在MO理论中,𝐻具有等于分子中基本AO的数量。在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。这些数值结果然后用于生成相关信息和图表。对于MO理论,输出包括MO能量图,确定最高占用和最低的无置置的MOS,即HOMO和LUMO,以及使用AO系数进行电子密度分布和键合分析的人群分析。紧密结合计算的结果产生了状态图的电子密度,这是电子能级的准连续分布,可以分解为来自各种轨道或原子成分的态密度,以及相应的FERMI水平,这是Homo的固态类似物的固态类似物。种群分析也可以进行,并提供用于识别重要键合特征的晶体轨道重叠种群(COOP)或汉密尔顿人群(COHP)图。最后,带结构图或能量分散曲线,这些曲线是沿波向量空间中特定方向的波形绘制的能量。