XiaoMi-AI文件搜索系统
World File Search System磁对撞机的磁铁 - 需要和计划内皮细胞转录的见解
颅内动脉瘤(IA)破裂是出血性中风的常见原因。未破坏的IAS的治疗是一个充满挑战的决定,需要微妙的风险分层。手术干预后(动脉瘤剪断)或血管内卷曲的临床结局率较差(分别分别为6.7%和4.8%),并且它们不提供防止IA的生长和破裂的保证。当前,没有药物治疗可以治愈或稳定IAS。改善当前或开发针对IA疾病的新疗法将需要更好地了解在疾病的不同阶段发生的细胞和分子机制。血液动力学在IA疾病中起关键作用。 虽然壁剪应力在IAS中的作用是完善的,但环状圆周拉伸(CC)的影响仍然需要透明度。 ias通常的特征是缺乏CC。 在这项研究中,我们试图了解动脉瘤CCS对内皮细胞功能(EC)功能及其在IA疾病中的显着意义的影响,认为CC可以影响CCS会影响壁层重塑。 RNA-Seq数据是生成的血液动力学在IA疾病中起关键作用。虽然壁剪应力在IAS中的作用是完善的,但环状圆周拉伸(CC)的影响仍然需要透明度。ias通常的特征是缺乏CC。在这项研究中,我们试图了解动脉瘤CCS对内皮细胞功能(EC)功能及其在IA疾病中的显着意义的影响,认为CC可以影响CCS会影响壁层重塑。RNA-Seq数据是生成
httpspps://www.sslslslslhd.health
临床试验活动计划(该计划)的目的是: - 提高证据支持临床护理 - 帮助患者与其健康状况相关的访问试验 - 使研究人员能够向澳大利亚患者提供国际试验,这一赠款机会的目标是提供财务援助的赠款,以提供支持澳大利亚的临床研究和临床研究的临床研究,以支持:澳大利亚的试用地点。- 提供高质量的证据,证明“通常的护理”环境中新型健康治疗,药物或设备的有效性,这将支持有关是否在澳大利亚环境中进行干预的决定。
博物馆空气。 - TROX
米开朗基罗的壁画也经历了一次大改造。在数个世纪的积尘之下,1508 年至 1512 年间的壁画重新焕发出了昔日的光彩和鲜艳的色彩。现在高对比度的色彩引发了激烈的争论,因为通常的柔和色调突然变成了明亮的色调。然而,米开朗基罗所参考的艺术和哲学模型证明了这种颜色和技术的选择。这重新引发了保护者和修复者之间的旧争论:艺术品应该恢复到原来的状态,还是应该带上岁月的光泽?
情绪健康及行为支持 (EWBS) 服务
创伤知情和依恋意识学校介绍这个复杂的主题。深入了解依恋和创伤,重点关注它们如何影响行为和学习。了解发展性创伤以及经历如何影响大脑发育,以及这在课堂和学校环境中可能是什么样子。将讨论和探索以关系方法和发展适应力为中心的策略。NB 创伤和依恋培训是诺森伯兰郡学校 CARE 计划的一部分,将由来自 EWBS、EPS 或 PMH 的两名专业人员领导。学校通过以通常的方式向 EWBS 提出全校请求来参加培训。
操纵城堡:以零售股票交易商的做市商为代价获利
关于操纵弊端的通常的言论强调了它的不公平和价格扭曲。但是,本文得出的结论是,旨在从内部化的人那里获利的策略没有引发任何严重的公平问题。同样令人惊讶的是,它得出结论,如果这些策略是自由发生的,它们可能会直接提高价格准确性。但是,这种影响在社会上比这种实践对流动性的负面影响更有价值。当人们添加从事这些策略和内部化的贸易商所消耗的资源以保护它们的资源时,这种负面的社会福利评估变得更加大得多,否则可以使用这些资源来为社会生产有价值的商品和服务。
发现和治疗早期严重的精神疾病
采用这种方法,经历了第一集精神病(FEP)的个人受到一个多学科团队的对待,以确保满足他们的需求。团队包括心理健康专业人员,职业和教育支持,家庭教育和支持以及护理管理。团队通常还包括自己在精神疾病中经历经验的人。该方法以个人的目标,需求和偏好为中心,并有时和为他们工作的地方与之满足。至关重要的是,个人及其确定的家庭都参与该过程。几项美国和国际研究表明,这种方法可以为通常的精神疾病治疗带来卓越的结果,特别是对于较短的未经治疗精神病的人而言。
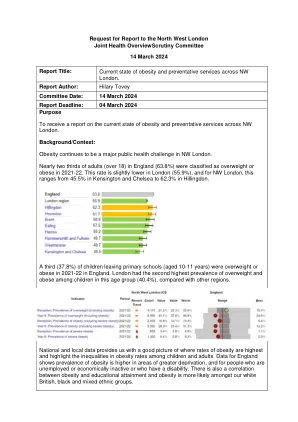
请求向西北伦敦联合健康报告提出报告...
这些运动是为了满足我们当地社区的需求而量身定制的。已经制定了许多健康的饮食资源和进餐计划,以制定预算紧张的人,并且已经制定了特定于文化的资源和文化适应的餐食计划。NW伦敦糖尿病转变计划还与Carbs&Cals合作资助了《世界书籍的发展》。《世界食品书》是第一个视觉资源,其中包括与当地社区共同设计的文化资源。关于体重管理和缓解的电影和资源已转化为通常的口语语言,包括乌尔都语,旁遮普语,阿拉伯语,索马里和印地语。
MAKO 无人机飞行模拟用于数据驱动的故障诊断
过去十年,各种用途的无人机数量迅速增加。这促使监管机构急于制定安全的整合战略,以适当共享空域的利用率。处理故障和失效是关键问题之一,因为它们在可用的事件报告中占了更大的比重。这些小型飞行器的硬件限制表明,需要使用分析冗余,而不是常规飞行中通常的硬件冗余做法。在本研究过程中,回顾了飞机的故障检测和诊断。然后模拟了 MAKO 飞机的非线性模型,以生成故障和正常飞行数据。该平台能够为各种飞行条件生成数据,并设计用于故障检测和诊断的机器学习实现。
马约拉纳费米子作为新出现的准粒子
其中,我们记为 σ µ = ( I, − σ i ) 和 ˆ σ µ = ( I, σ i )。σ i 是通常的泡利矩阵。在以下的讨论中,我们将处处使用外尔基。现在我们考虑能量为 E(可以为正数或负数)的狄拉克方程的稳态解,它们不过是 Ψ( x ) = e − i Et Φ E ( x )。这里,Φ E ( x ) 满足狄拉克方程 ( 1 ),只是 i∂ 0 处处被 E 取代。稳态提供了一个完整的基础,任何一般解 Ψ( x ) 都可以根据它展开。此外,它们帮助我们看到狄拉克方程的一个重要的内部对称性,称为电荷共轭对称性。如果 Φ(x) 是与能量 E 相关的状态,我们可以找到相应的电荷共轭态,定义为