XiaoMi-AI文件搜索系统
World File Search System量子化
探测无序量子的空穴自旋输运 - ePrints Soton
摘要。由于无序量子点的强轨道量子化，在标准 p 型硅晶体管中可以实现单空穴传输和自旋检测。通过使用充当伪栅极的阱，我们发现了表现出泡利自旋阻塞的双量子点系统的形成，并研究了漏电流的磁场依赖性。这使得可以确定空穴自旋状态控制的关键属性，其中我们计算出隧道耦合 tc 为 57 µ eV，短自旋轨道长度 l SO 为 250 nm。使用无序量子点时，界面处表现出的强自旋轨道相互作用支持电场介导控制。这些结果进一步激励我们，可以使用易于扩展的平台（例如行业标准硅技术）来研究对量子信息处理有用的相互作用。
单光子相干反馈控制与滤波
如果一个光场恰好包含 k 个光子，则它处于 k -光子态。由于其高度量子化的特性，光子态在量子通信、计算、计量和模拟方面有着广阔的应用前景。最近，人们对各种光子态的产生和操纵的兴趣日益浓厚。控制工程领域的一个新的重要问题是：如何分析和合成由光子态驱动的量子系统以实现预定的控制性能？在本综述中，我们引入了单光子态，并展示了量子线性系统如何处理单光子输入，以及如何使用线性相干反馈网络来塑造单光子的时间脉冲。我们还介绍了一种单光子滤波器。（本综述的扩展版本可在 arXiv:1902.10961 找到。）
纯量子状态估计的最小正常基碱基
量子状态估计[1]，即概念确定量子系统的完整说明的过程，对于NUMER应用至关重要，范围从量子化处理处理到量子模拟。在D维量子系统中，可以通过带有单位迹线的阳性半明确复合物来描述状态。因此，量子状态估计需要了解至少D 2-1线性独立的遗产运算符的期望值。传统的提出这些期望值的方法是测量D 2-1广义的Gell-Mann矩阵[2，3]。但是，这种方法需要大量的实验资源和D大范围的时间。一种替代方法是测量d + 1个不偏的碱基[4-8]。虽然此组提供了更好的缩放，但它仍然是线性的，并且它不知道是否存在相互无偏的基础
从光到量子物理学
摘要在本文中，我们提出了一种新的最小数学概念方法，用于使用光两极化的量子力学，以使中学学生对量子化，以使学生更接近所谓的量子力学思维方式。我们调查了学生如何思考一些基本概念和基本定律，我们发现某些概念在年轻的年龄段也是可以理解的。我们研究了所谓的状态圈的引入，它可以忠实地代表量子机械形式主义，而无需让学生参与抽象代数计算。然后，我们对学生对叠加原则和缺乏轨迹的想法进行了分类和分析，发现测量和缺乏轨迹的概念是有问题的。我们探讨了年轻的学生倾向于拥有类似格式塔的量子概念的心理模型，同时也能够正确地使用可视化量来在量子领域进行推理。总的来说，本文提供了最早在中学中引入量子力学基本特征的证据。
量子间相关性的研究......
量子物理学家和神经科学家一直试图从人脑中寻找相关的量子效应。Umezawa 等提出脑细胞中存在量子动力学自由度空间分布完全有序的可能性，并针对多脑细胞系统提出了改善量子动力学自由度空间分布的物理模型 [2]。彭罗斯和萨梅罗夫的意识量子模型（ORCH OR）认为意识产生于细胞膜微管中，蛋白质电子是产生意识活动的场所。1963 年诺贝尔物理学奖获得者维格纳认为意识可以通过波函数坍缩，使不确定状态转变为确定状态，从而改变客观世界。英国南安普顿大学的脑电图（EEG）实验证实，思维过程本质上是量子化的 [3, 4]。越来越多的物理学家和认知科学家认为量子和意识之间存在着深刻而重要的内在联系。
增强具有生成深度学习的定量光声断层扫描的合成训练数据
用作变量ANSATZE的参数化量子电路正在成为有前途的工具，可以解决从量子化学到组合优化的复杂问题。这些变异的量子电路可能会遭受贫瘠的高原诅咒的困扰，其特征是具有系统尺寸的成本功能梯度的指数消失，这使得对实用应用不可行。由于无法有效地模拟通用量子电路，因此确定其训练性是一个重要的问题。在这里，我们找到了一种有效的方法来计算成本函数的梯度及其对各种变异量子电路的差异。我们的计划依赖于我们的证明，证明了从随机初始化电路到一组克利福德电路的精确映射，这些电路可以通过著名的Gottesmann-Knill定理在经典计算机上有效模拟。此方法是可扩展的，可用于证明各种量子电路的训练性，并探索可以克服贫瘠高原问题的设计策略。作为说明性示例，我们显示了最多100吨的结果。
![arXiv:2203.11846v2 [gr-qc] 2022 年 3 月 23 日](/simg/g:\will\search\icon\source\3\33237c1efc87d349075d0cb5ec00030b4d72744d.webp)
arXiv:2203.11846v2 [gr-qc] 2022 年 3 月 23 日
近年来，在基础概念提案 [1–3] 的基础上，许多作者讨论了进行实验室规模实验以探究引力量子性质的关键问题的想法 [4]。这些实验旨在检验微扰量子化广义相对论（被视为有效的量子场论 [5–8]）是否正确描述了低能下的自然。已经提出了许多替代方案。其中包括涉及量子力学引力崩溃的模型 [9, 10]、混合经典-量子模型 [11–13]、引力作为一种新兴力量的模型 1 [15, 16]，以及关于红外全息效应的想法 [17, 18]。在未来十年内可能实现的实验可以对这些模型做出决定性的陈述。在这份 Snowmass 白皮书中，我们简要概述了这个新兴的研究计划。我们对理论问题和实验实现提供了非详尽的展望，重点关注未来十年的主要未决问题和研究机会。我们特别强调需要详细的、理论一致的红外重力模型，该模型不同于标准引力子有效场理论。
随机电路中的量子魔法动力学
摘要 魔力指的是一个系统中“量子化”的程度，它不能仅通过稳定态和 Clifford 操作来完全描述。在量子计算中，稳定态和 Clifford 操作可以在经典计算机上有效地模拟，即使它们从纠缠的角度看起来很复杂。从这个意义上说，魔力是释放量子计算机独特计算能力以解决经典难以解决的问题的关键资源。魔力可以通过满足 Clifford 操作下单调性等基本性质的度量来量化，例如 Wigner 负性和 mana。在本文中，我们将随机电路的统计力学映射方法推广到 R´enyi Wigner 负性和 mana 的计算。基于此，我们发现：（1）一个精确的公式描述在 Haar 随机电路下制备的多体态中魔力与纠缠之间的竞争；（2）一个公式描述在随机 Clifford 电路下演化的状态中魔力的扩散和扰乱； (3) 定量描述测量条件下的魔法“压缩”和“隐形传态”。最后，我们评论了相干信息与魔法之间的关系。
无辅助量子位的多对数深度控制非门
受控操作是量子算法的基本组成部分。将 n 个控制非门 (C n (X)) 分解为任意单量子比特和 CNOT 门是一项重要但并非易事的任务。本研究引入的 C n (X) 电路在渐近和非渐近范围内的表现优于以前的方法。提出了三种不同的分解：一种是使用一个借用的辅助量子比特的精确分解，电路深度为 ΘðlogðnÞ3Þ，一种没有辅助量子比特的近似分解，电路深度为 OðlogðnÞ3logð1=ϵÞÞ，以及一种具有可调深度电路的精确分解，该电路的深度随着可用辅助量子比特的数量 m ≤ n 而减少，即 Oðlogðn=bm=2cÞ3+logðbm=2cÞÞ。由此产生的指数加速可能会对容错量子计算产生重大影响，因为它可以改善无数量子算法的复杂性，应用范围从量子化学到物理学、金融和量子机器学习。
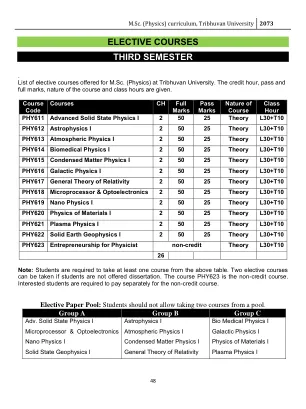
选修课程 - TU 登录门户 - 特里布万大学
物理学。课程内容：1. 简介：[2 小时] 1.1 非相互作用电子气。2. Born-Oppenhemier 近似：[3 小时] 2.1 基本哈密顿量，2.2 绝热近似，2.3 简化电子问题。3. 二次量子化：[5 小时] 3.1 玻色子，3.2 费米子，3.3 费米子算符。4. Hartree-Fock 近似：[4 小时] 4.1 非相互作用极限，4.2 Hartree-Fock 近似，4.3 图表。5. 相互作用电子气：[4 小时] 5.1 均匀电子气，5.2 Hartree-Fock 激发谱，5.3 金属的结合能。 6. 金属中的局部磁矩：[4 小时] 6.1 局部矩：现象学，6.2 平均场解。 7. 局部矩的猝灭：[8 小时] 7.1 近藤问题，7.2 近藤汉密尔顿量，7.3 为什么 J 为负？ 7.4 散射和电阻率最小值，7.5 电子-杂质散射振幅，7.6 近藤温度。