XiaoMi-AI文件搜索系统
World File Search System基于药代动力学的草药 - 药物互动
摘要简介/目标。草药一直是整个人类历史上至关重要的可再生医学来源,因为大部分全球人口仍然取决于它们的健康益处。草药补充剂的日益普及引起了人们对与其他药物原位的总体安全性和潜在互动的明显关注。目的是刺激对草药 - 药物相互作用的未来研究,以及了解这种相互作用的后果的相互作用机制。方法。该审查是通过使用Google Scholar,Science Direct,Mendeley,Scopus和PubMed的数据库进行系统搜索进行的。用英语编写的出版物被使用。据报道,许多草药产品与已知的东正教药物相互作用。抑制诱导机制触发链反应,通常导致药物生物利用度,毒性或不良副作用降低。据报道,一些草药植物构成结合了CYP2C9,CYP2C19,CYP2E1和CYP3A1,以及许多其他暂时或不可逆地结合了CYP3A1。结论。这项研究是通过重申常规和定期向医生和患者提供固有危险(例如降低疗效和与Herb-Drug相互作用(HDI)相关的毒性增加)的不完善性结束的结论。草药使用者应定期建议适当使用草药补充剂,以避免在共同给药期间或联合疗法中发生不良药物相互作用的风险。在HDI中可以观察到协同作用和拮抗作用,因此需要进一步的临床前和临床经验研究来强调HDI的机制和程度。关键字:草药 - 药物相互作用,酶,药代动力学互动,传统医学,细胞色素P450通讯作者:Mary O. Ologe电子邮件:FunMiologe@yahoo.com
Nest Learning Thermostat(第 4 代)Pro 安装指南(...
智能计划会随着时间的推移从用户的温度调节和存在模式中学习,以创建自定义的温度计划。Nest Learning Thermostat(第 4 代)将建议更改用户的计划,以优化舒适度和节能效果。用户可以允许 Nest Learning Thermostat(第 4 代)自动应用这些更改,先查看,然后接受或拒绝建议,或完全禁用智能计划。智能计划在使用的第一周内会学习最多,但永远不会停止学习。即使选择了“自动应用”,当恒温器更改其计划时,用户也会始终收到通知。当恒温器从用户的手动温度调节中“学习”时,恒温器也会在恒温器和应用程序中以视觉方式指示。用户可以随时查看 Google Home 应用程序中的“历史记录”标签,查看何时进行了更改。如果用户的习惯或计划发生了重大变化,用户可以重置智能计划学习,从那时起,恒温器将开始学习他们的偏好。
肾功能受损患者的药代动力学
在一项药代动力学研究中,非人类灵长类动物的两项实验室研究,有25种成年普通摩尔果会接受单个平方剂量的丁丙诺啡SR(0.15 mg/kg,n = 8)或ethiqa Xr(0.1 mg/kg,n = 6,n = 6,0.15 mg/kg,n = 6,0.15 mg/kg,n = 3,和0.2 mg/kg/kg/kg/kg/kg,根据红斑和肿胀的总检查对注射部位反应进行评分。在所有组的剂量后8小时和24小时内都注意到轻度镇静。体重相对于基线的体重在所有组的基线均减少,除了ethiqa XR 0.15 mg/kg;但是,这些减少在临床上并不显着(<占体重的10%)。对任何一种配方的注射div>粉末载导致剂量依赖性的笼子运动增加。丁丙诺啡SR和埃塞卡XR急性注射部位均表现出急性坏死和炎症。慢性两种药物的炎症程度总体相似。但是,在质上有所不同。Burprenorphine SR注射部位主要与巨噬细胞和中性粒细胞相关,而埃塞克XR位点与巨噬细胞和多核巨细胞和胆固醇裂解有关,响应于车辆培养基。6
W*-代数上的参数模型和信息几何
在经典几何和量子信息几何中,通常处理概率分布或量子态的参数化子集,俗称参数模型。经典背景下的典型例子是高斯概率分布族,在量子背景下的典型例子是量子相干态族。从概念和实践的角度来看,都可能存在物理理论约束,导致只有某些概率分布或量子态才能被建模或物理实现(再想想高斯概率分布和量子相干态),因此证明选择参数模型是合理的。另一方面,从纯数学的角度来看,如果我们想利用标准微分几何的数学形式,就必须选择参数模型[1,43,50]。事实上,可测结果空间上的概率分布空间和等同于复可分希尔伯特空间上的密度算子空间的量子态空间都不具备光滑流形的结构。颇有意思的是,这在有限维中已经发生了:在经典情况下,离散有限结果空间 X n(有 n 个元素)上的概率分布空间可以自然地等同于 R n 中的单位单纯形,后者是带角的光滑流形的典型例子 [54];在量子情况下,等同于有限维复希尔伯特空间 H 上的密度算子空间的量子态空间,当 dim ( H ) = 2 [ 11 , 35 ] 时,是具有边界的光滑流形,称为布洛赫球;当 dim ( H ) > 2 [ 24 ] 时,是分层流形。在无限维中,考虑到无限维微分几何的技术细节,情况甚至更糟。尽管可以说在经典 [ 64 ] 和量子 [ 42 ] 中都有旨在建立无限维非参数理论的方法,但我们认为它们实际上是参数模型,其中参数位于无限维流形中。事实上,Pistone 和 Sempi [ 64 ] 的开创性工作处理的不是测度空间上整个概率分布空间上的 Banach 流形结构,而是关于给定参考概率测度 μ 相互绝对连续的所有概率分布空间上的 Banach 流形结构。显然,这种选择可以合理地称为概率分布的参数模型。 Jencova [ 42 ] 的工作中也发生了类似的事情,其中 Banach 流形结构不是赋予 W ⋆ -代数 A 上的整个状态空间,而是赋予 A 上的忠实正常状态空间。因此,为了使用标准微分几何的工具,正如在经典几何和量子信息几何中惯常的做法一样 [4、5、51、58、67],我们必须接受使用参数模型的必要性。经典情况在无限维环境中也得到了彻底和系统的研究 [7-9],而据我们所知,量子态参数模型的信息几何(特别是在无限维环境中)仍未得到充分探索。这项工作的目的是开始探索这片土地,并以这样一种方式进行,即可以同时处理经典情况和量子情况。关键
拉格斯代尔太阳能公园
EDPR NA 是可再生能源领域的全球领导者 EDP Renewables (Euronext: EDPR) 的全资子公司。EDPR 是全球第四大风能和太阳能生产商,业务遍及欧洲、北美、南美和亚太地区的 28 个市场。EDPR 总部位于马德里,在休斯顿、圣保罗和新加坡设有主要地区办事处,在可再生能源领域拥有顶级资产的完善开发组合和市场领先的运营能力。特别值得注意的是陆上风电、分布式和公用事业规模的太阳能、海上风电(OW - 通过 50/50 合资企业)以及补充可再生能源的技术,例如存储和绿色氢能。
博士论文药代动力学-药效学建模...
联合药物疗法是成功治疗多种疾病的关键,在这些疾病中单一疗法效果不够好或出现了耐药性。因此,开发新的药物组合是主要关注点。固定剂量组合也是如此,近年来批准的固定剂量组合有所增加。开发固定剂量组合通常需要进行大规模析因设计研究以验证组合的疗效。随着对药物个性化的更多关注,需要为患者提供几种剂量水平的固定剂量组合。对于析因设计研究,这将导致非常昂贵的临床试验。为了降低开发成本并指导药物开发,必须验证现有工具并开发新工具。然而,用于分析固定剂量组合的此类基于模型的工具还处于起步阶段。
C 代数值 Sb 度量空间及其应用...
1922 年,Stefan Banach 建立了一个重要的不动点定理,即巴拿赫收缩原理 (Banach 收缩原理),它是分析学的基本结果之一,也是不动点理论的基本公理。BCP 吸引了众多数学家的注意,并由此产生了各种应用和扩展。1993 年,Czerwik 引入了半度量空间的新起源 [3]。此后,许多作者研究了此类空间中的不动点理论 [1,2,5,14]。此外,Xia [19] 将这些空间称为 b 度量空间。有关该空间的更多信息,请参见 [6]。最近,在 [8] 中,作者引入了 C ∗ -代数值度量空间的概念。事实上,实数集的研究已经过渡到单元 C ∗ -代数的所有正元素的框架。在 [ 7 ] 中,作为 b -度量空间和算子值度量空间 [ 9 ] 的推广,作者引入了一类新的度量空间,即 C ∗ -代数值 b -度量空间,并给出了此类空间中满足压缩条件的自映射的一些不动点结果。
阿米代尔地方住房战略 2024
在这方面,为了支持协调一致、具有成本效益地释放土地和基础设施,在寻求对位于增长区内第 0-2 阶段以外的土地进行任何重新分区之前,应更新战略以确定需求和需求,以及土地的特定地点开发限制,并将更新后的战略提交给该部门批准。与该部门以及初级产业和区域发展部、新南威尔士州交通部和新南威尔士州生物多样性、保护和科学小组等主要机构的持续合作对于成功实施该战略至关重要。我鼓励理事会积极参与并与这些机构合作,讨论潜在的高环境土地、重要农田、易受洪水侵袭的土地、交通管理和无障碍计划等问题。如果您希望进一步讨论此事,欢迎致电 6643 6410 联系该部门的规划官 Sam Tarrant 先生。此致
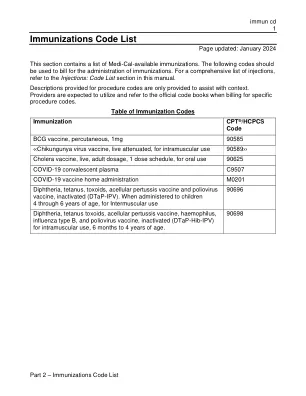
免疫接种代码表 (immun cd)
日本脑炎病毒灭活疫苗,肌肉注射用 90738 麻疹/腮腺炎/风疹病毒活疫苗 (MMR) 90707 麻疹、腮腺炎、风疹和水痘活疫苗 (MMRV) 90710 脑膜炎球菌结合疫苗,血清群 A、C、Y 和 W-135,四价(MCV4 或 MenACWY)