XiaoMi-AI文件搜索系统
World File Search System随机过程和遗传阈值效应如何解释不完整的渗透率并为因果疾病机制提供信息?
抽象不完整的渗透性是孟德尔病的规则而不是例外。在综合症单基因疾病中,表型变异性可以看作是多个独立临床特征的不完全渗透性的组合。在遗传学相同的个体中,例如等源性模型生物,根据遗传阈值模型,分子和细胞水平的随机变化是渗透不完全渗透的主要原因。通过定义因果生物学读数和遗传责任值的特定概率分布,随机性和不完整的渗透率提供了有关生物系统中阈值的信息。通过同时对相对简单的表型和单个细胞水平的分子读数进行定量,可以确定阈值的确定阈值。然而,仅使用实验和还原主义方法,对于复杂的形态表型而言,这是更具挑战性的,在这种方法上,因果和效应在时间上分开以及多种生物学模式和尺度。在这里,我考虑如何将观察数据与高置信度因果模型整合在一起的因果推断,可以用来量化不同随机变化来源对表型多样性的相对贡献。总体而言,这些方法可以为疾病机制提供依据,改善了临床结果的预测,并优先考虑基因功能模式和尺度的基因治疗靶标。
M. Tech。微电子 b''
co1应用与统计推断有关的概念,例如随机抽样和采样分布。CO2根据样本估算分布的参数,并进行假设检验,回归分析,相关性和方差分析。 CO3应用数学和统计数据的全面知识来解决静态概率,动态概率的问题。 CO4使用随机过程的知识,提出现实生活中的问题并确定长期概率。 co5基于毒物过程,估计排队系统统计推断的各种性能度量:随机抽样,抽样分布,参数估计和假设检验,回归,相关性和方差的相关性和分析 - 示例 - 示例。 静态概率,动态概率。 状态分类,马尔可夫过程的链。 马尔可夫系统的稳定性,限制行为,随机步行。 泊松过程:假设和衍生,相关分布,出生和死亡过程。 排队系统,一般概念,M/M/1模型和M/M/S,稳态行为,瞬态行为。 参考:1。 Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。 J.Medhi,“随机过程”。 3。 A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,CO2根据样本估算分布的参数,并进行假设检验,回归分析,相关性和方差分析。CO3应用数学和统计数据的全面知识来解决静态概率,动态概率的问题。CO4使用随机过程的知识,提出现实生活中的问题并确定长期概率。co5基于毒物过程,估计排队系统统计推断的各种性能度量:随机抽样,抽样分布,参数估计和假设检验,回归,相关性和方差的相关性和分析 - 示例 - 示例。静态概率,动态概率。状态分类,马尔可夫过程的链。马尔可夫系统的稳定性,限制行为,随机步行。泊松过程:假设和衍生,相关分布,出生和死亡过程。排队系统,一般概念,M/M/1模型和M/M/S,稳态行为,瞬态行为。参考:1。Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。 J.Medhi,“随机过程”。 3。 A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。J.Medhi,“随机过程”。3。A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,A. Papoulis和S.U.Pillai,概率,随机变量和随机过程,
模块 1 概率讲座 1-6 主题 1.1 ...
在我们的日常生活中,我们会遇到许多无法预测其性质的过程。此类过程称为随机过程。获取有关随机过程的信息的唯一方法是进行实验。每次这样的实验都会产生无法预测的结果。事实上,即使在相同条件下重复实验,由于存在无法控制的因素,实验结果也可能因试验而异。但是,我们可以提前知道实验的每个结果将导致几种给定可能性中的一种。例如,在固定环境下投掷骰子时,结果(骰子上表面的点数)无法提前预测,并且每次试验都会有所不同。但是,我们事先知道结果必须是数字 1、2、...、6 中的一个。概率论涉及随机过程的建模和研究。统计学领域与概率论密切相关,它涉及从与随机过程相关的数据中得出推论。
面板结构2024调用物理科学和工程
与COG和ADG方案中资助的人相比,在STG项目中使用了更多的几何形状,数学物理,微分方程和图理论,而离散的数学和随机过程在COG项目和数字理论中使用了更多的数学和随机过程,应用的数学和量子现场理论在ADG Projects
课程和教学大纲
线性方程的线性代数系统:矩阵的范围空间和空空间,矩阵的等级,线性方程系统的解决方案的存在和唯一性,与线性方程系统相关的解决方案空间的尺寸。向量空间:向量空间,子空间,双空间,内核,空空间,线性独立性和依赖性,线性跨度,基础,维度,直接总和,线性变换。矩阵表示:特征值和特征向量,相似性,等级和无效,对角线化,约旦形式。随机变量和随机过程随机变量,分布和密度函数,力矩和力矩生成功能,多元分布,独立的随机变量,边际和条件分布,条件期望,随机变量的转换,随机变量的转换,随机过程的元素,随机过程的元素,一般随机过程的分类。马尔可夫链:定义,示例,过渡概率,状态和链的分类,基本限制定理,限制马尔可夫链的分布。ODE的ODE和计算系统的系统:通过Lipchitz条件,解决方案和稳定性的解决方案的存在和独特性。变化的计算:变分问题的示例,变异问题的基本计算,弱和强大的极端和强大的终点问题,哈密顿量。参考:
(离散)扩散的顺序蒙特卡洛指导...
扩散模型已成为机器学习中生成建模的重要方法。这些模型是通过模拟一些“破坏性”随机过程来训练的,这些随机过程在训练数据样本中初始化,并且具有易于采样的限制分布。通过学习如何逆转随机过程来获得生成模型。扩散模型的大多数应用都用于连续数据,并使用高斯扩散作为随机过程。但是,相同的想法也可以通过适当的破坏过程选择,例如基于离散的马尔可夫链和吸收状态的引入。通过指导进一步提高了扩散生成模型的性能和适用性,这是一种基于某些辅助信息或外部模型来指导生成过程的技术。指导既可以用于有条件生成(例如带有分类器指导)和改善样本质量(鉴别器指导)。在本演讲中,我将讨论如何将顺序的蒙特卡洛用于扩散模型的指导。我将重点放在不容易适用的基于常规得分的指导技术的离散设置上。基于与FilipEkströmKelvinius的联合工作(自回旋扩散模型的歧视指南,AISTATS 2024,https://arxiv.org/abs/2310.15817)
AFV防御:2021年6月29日1装甲战斗车队的绩效预测,以导演的能量武器
最近的一项研究引入了一项程序,以量化一支装甲车辆团队的生存能力,当时它对一次导弹攻击进行。尤其是本研究调查了协作主动保护系统的概念,重点介绍了高功率射频定向能源武器提供的车辆防御的情况。当前论文的目的是证明如何扩展该分析以考虑多个导弹威胁。这是通过引入跳跃随机过程来实现的,该过程代表在给定时间瞬间击败的导弹数量。分析是通过考虑此随机过程的居民时间进行的,并显示了对这些跳跃时间的考虑如何与辅助随机过程的过渡概率有关。后一个概率随后与检测和导弹威胁的破坏的概率有关。这些居住时间的总和可以在任何给定时间瞬间量化团队的生存能力。由于在本文的背景下对高能量激光器的应用非常感兴趣,因此数值示例将集中在这种定向的能量武器上,以用于装甲的车辆团队防御。
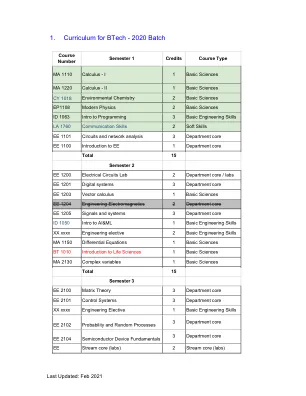
1。BTECH的课程-2020 Batch
这些课程与EE课程中的核心课程具有显着的重叠(> 60%)。因此,普通的EE学生不应根据任何“选修”类型选择他们。但是,允许替换后的BTECH电气工程和分支更换器进入EE。这有助于改变分支机构,以迅速赶上第一学期的错过课程。1。EE1101电路和网络分析可以用EE1102-BASIC电气工程取代2。 EE1201数字系统可以用EE1202数字电路代替3。 EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1101电路和网络分析可以用EE1102-BASIC电气工程取代2。EE1201数字系统可以用EE1202数字电路代替3。 EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1201数字系统可以用EE1202数字电路代替3。EE1205信号和系统可以用EE1206线性系统和信号处理代替。 4。 EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE1205信号和系统可以用EE1206线性系统和信号处理代替。4。EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。 3。 a)不允许的课程列表,因为EE BTECH学生的部门选修课EE2102验证性和随机过程可以用EE2103验证性和随机变量代替。3。a)不允许的课程列表,因为EE BTECH学生的部门选修课