XiaoMi-AI文件搜索系统
World File Search System揭示绿色主张:自愿绿色电力市场供需时间更紧密协调的影响
自 1977 年以来,能源与环境政策研究中心 (CEEPR) 一直是麻省理工学院能源与环境政策研究的焦点。CEEPR 提倡严谨客观的研究,以改善政府和私营部门的决策,并通过与全球行业伙伴的密切合作确保其工作的相关性。利用麻省理工学院无与伦比的资源,附属教职员工和研究人员以及国际研究伙伴为与能源供应、能源需求和环境相关的广泛政策问题进行实证研究。麻省理工学院 CEEPR 工作论文系列是这些研究工作的重要传播渠道。CEEPR 发布由麻省理工学院和其他学术机构的研究人员撰写的工作论文,以便及时考虑和回应能源和环境政策研究,但在发布之前不进行选择过程或同行评审。因此,CEEPR 发布工作论文并不构成对工作论文准确性或优点的认可。如果您对某篇工作论文有疑问,请联系作者或其所在机构。
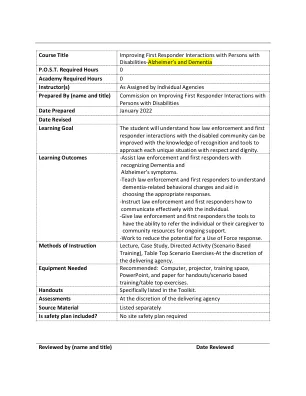
课程名称 改善急救人员与残疾人士(阿尔茨海默氏症和痴呆症)的互动 POST 所需时数 0 学院要求
课程名称 改善急救人员与残疾人士的互动-阿尔茨海默氏症和痴呆症 POST 所需学时 0 学院所需学时 0 讲师由各个机构指定 编写者(姓名和职称)改善急救人员与残疾人士互动委员会 编写日期 2022 年 1 月 修订日期 学习目标 学生将了解如何通过掌握识别知识和工具来改善执法部门和急救人员与残疾人社区的互动,以便以尊重和尊严的方式处理每种独特情况。 学习成果 - 协助执法部门和急救人员识别痴呆症和阿尔茨海默氏症的症状。 - 教导执法部门和急救人员了解与痴呆症相关的行为变化并帮助他们选择适当的反应。 - 指导执法部门和急救人员如何与个人进行有效沟通。 - 为执法部门和急救人员提供工具,使他们能够将个人或其照顾者转介给社区资源以获得持续支持。 -努力降低使用武力反应的可能性。教学方法讲座、案例研究、指导活动(基于情景的培训)、桌面情景练习-由交付机构决定。所需设备推荐:计算机、投影仪、培训空间、PowerPoint 和用于讲义/基于情景的培训/桌面练习的纸张。讲义在工具包中具体列出。评估由交付机构决定来源材料单独列出是否包括安全计划?不需要现场安全计划
实现单一操作所需时间的上限
场,这样的下限并不能提供太多关于完成这项任务最多需要多少时间的见解。因此,非常需要 T 的上限。这样的上限应该取决于目标幺正变换、描述所考虑量子系统的哈密顿量、可用于实现目标变换的控制数量以及可能的约束,比如控制场中的能量和带宽。显然,如果描述 d 维量子系统的哈密顿量的每个矩阵元素都可以瞬间任意控制,则幺正群 U(d) 中的每个幺正变换都可以通过控制每个矩阵元素的 d2 个(无约束)经典场瞬间实现。但是,如果我们对所考虑的系统只有受限的访问,会怎么样呢?有多少个控制以及哪些控制允许在最多 O(poly(d)) 的时间内实现每个 Ug∈U(d)?这里我们证明,如果描述 d 维量子系统的哈密顿量的对角线元素可以通过经典场进行一般控制,并且如果该系统可由这些场控制,则实现每个幺正操作的时间最多为 O(d3)。然而,我们注意到,对于由 n 个量子比特(即 d=2n)组成的量子比特系统,我们的上限关于 n 呈指数增长。这并不奇怪,因为实现一般幺正变换的时间 T 会随着量子比特的数量而呈指数增长,这可以追溯到大多数幺正操作无法有效实现的事实,即时间会随着量子比特的数量而呈多项式增长 [2]。有关时间最优控制和量子计算的进一步阅读,我们参考了开创性著作 [ 3 , 4 ],而量子比特系统的 T 的上限则在 [ 5 ] 中得到开发。虽然在这项工作中我们主要关注由描述四维量子系统的一组基态 {| n ⟩ } 确定的网络,但我们也考虑了将其推广到由量子比特组成的网络。这里关联图不是由两个键之间的耦合确定,而是由通过任意二体相互作用项耦合的量子比特确定。基于创建特定幺正变换所需的 CNOT 门数量 [ 6 – 8 ],我们还提供了 T 的上限,以使用 2 n 个局部控制在 -量子比特网络上实现给定的 U g。获得 T 上限的一种方法是找到与某些控制应用相对应的门序列,从而创建通用幺正变换。确定实现该序列所需的相应时间的上限,然后得出实现通用酉变换的上限。例如,该策略具有已成功应用于 -量子比特网络,以表征使用 2 n 个局部控制在最多多项式时间内实现的门集 [ 5 ]。这里我们基于 [ 5 ] 中提出的概念,并展示了由哈密顿量描述的 d 维量子系统