XiaoMi-AI文件搜索系统
World File Search System马卡罗夫
护士教育者 - 西卡罗来纳大学
申请流程 1. 在 westerngrad.com 上在线申请。您需要提交成绩单、GRE 或 MAT 成绩、3 封推荐信、专业陈述、简历和申请费。有关推荐信、专业陈述和简历的具体说明可在申请网站上找到。
护士教育者 - 西卡罗来纳大学
申请流程 1. 在 westerngrad.com 上在线申请。您将被要求提交您的成绩单、GRE 或 MAT 成绩、3 封推荐信、专业陈述、简历和申请费。有关推荐信、专业陈述和简历的具体说明可在申请网站上找到。
基于蒙特卡罗的电力可靠性评估方法...
摘要 — 在基于任务概况的可靠性评估中，计算表示电力电子转换器热应力的静态参数是一种常用方法。这些参数随后用于蒙特卡罗 (MC) 模拟，以估计考虑到变化的电力转换器中组件的预期寿命。然而，静态参数并不总是代表电力转换器中组件的实际现场运行条件。为了克服这一限制，本文在 MC 模拟中使用的动态任务概况特性中实施了两种引入参数方差的方法。在两种不同的应用案例中，证明了使用静态参数会在 MC 模拟中引入显著误差。对于光伏 (PV) 逆变器应用，如果使用静态参数，半导体的寿命可能会被高估高达 30%，而对于不间断电源 (UPS) 系统应用，这种差异可能达到近 50%。索引术语 — 转换器可靠性、寿命预测、任务概况、蒙特卡罗方法。
蒙特卡罗中的随机信标：效率
定期访问不可预测且抗偏差的随机性对于区块链、投票和安全分布式计算等应用非常重要。分布式随机信标协议通过在多个节点之间分配信任来满足这一需求，其中大多数节点被认为是诚实的。区块链领域的众多应用促成了几种分布式随机信标协议的提出，其中一些已经实现。然而，许多当前的随机信标系统依赖于阈值加密设置或表现出高昂的计算成本，而其他系统则期望网络是部分或有界同步的。为了克服这些限制，我们提出了 HashRand，这是一种计算和通信效率高的异步随机信标协议，它只需要安全哈希和成对安全通道即可生成信标。HashRand 的每个节点摊销通信复杂度为每个信标 O(𝜆𝑛 log (𝑛)) 位。 HashRand 的计算效率归因于单向哈希计算比离散对数指数计算的时间少两个数量级。有趣的是，除了减少开销之外，HashRand 还利用安全哈希函数对抗量子对手，实现了后量子安全性，使其有别于使用离散对数加密的其他随机信标协议。在一个由 𝑛 = 136 个节点组成的地理分布式测试平台中，HashRand 每分钟产生 78 个信标，这至少是 Spurt [IEEE S&P'22] 的 5 倍。我们还通过实施后量子安全异步 SMR 协议展示了 HashRand 的实际效用，该协议在 𝑛 = 16 个节点的 WAN 上的响应率为每秒超过 135k 个事务，延迟为 2.3 秒。
二次量子变分蒙特卡罗
本文介绍了二次量子变分蒙特卡罗 (Q 2 VMC) 算法，这是量子化学中的一种创新算法，可显著提高求解薛定谔方程的效率和准确性。受虚时间薛定谔演化的离散化启发，Q 2 VMC 采用了一种新颖的二次更新机制，可与基于神经网络的假设无缝集成。我们进行了大量的实验，展示了 Q 2 VMC 的卓越性能，在跨各种分子系统的波函数优化中实现了更快的收敛速度和更低的基态能量，而无需额外的计算成本。这项研究不仅推动了计算量子化学领域的发展，还强调了离散化演化在变分量子算法中的重要作用，为未来的量子研究提供了一个可扩展且强大的框架。
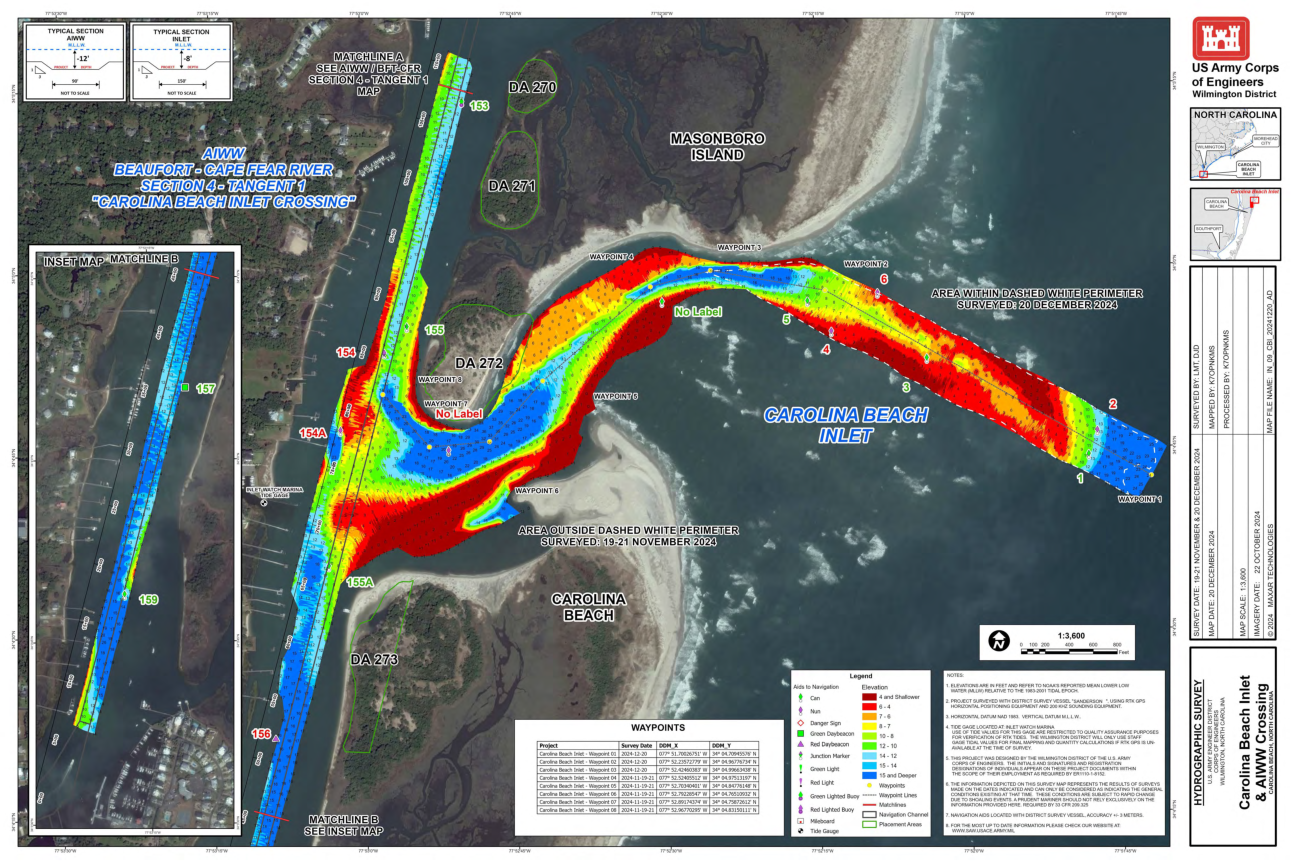
卡罗莱纳海滩入口 - 美国陆军工程兵团
5. 此项目由美国陆军工程兵团威尔明顿区设计。个人姓名首字母和签名以及注册 C) 职务名称出现在这些项目文件中，属于 ER1110-1-8152 所要求的 IR 工作范围内。0 a::: 6. 此测量地图上描述的信息代表在所示日期进行的测量结果，只能被视为表明当时存在的一般 C 条件 E。这些条件可能会因浅水事件而迅速变化。谨慎的海员不应完全依赖 > :::c 此处提供的信息。33 CFR 209.325 要求
用于量子蒙特卡罗模拟的 Metropolis 方法
尽管 Metropolis 等人的方法[1] 最初应用于经典的硬盘系统，但后来发现该算法对于许多不同的应用都是必不可少的。在本次演讲中，我将讨论 Metropolis 算法在量子多体问题中的一些应用。本文将严格限制在量子蒙特卡罗 (QMC) 中 Metropolis 拒绝方法的使用，而不讨论 QMC 的其他方面。Metropolis 算法的丰富性和本文的简洁性意味着我只能简要介绍这些发展中的一小部分，并且必须局限于肤浅的讨论。其他人将讨论它在凝聚态物质和格点规范理论的量子格点模型中的应用，因此我将重点关注非相对论连续体应用，特别是需要推广基本 Metropolis 算法的发展。我将只简要提及这些应用背后的物理学，而不是参考评论文章。我们对 Metropolis 算法的定义如下。假设 s 是相空间中的一个点，我们希望对分布函数 π ( s ) 进行采样。在最简单的算法中，只有一个转移概率：T ( s → s ′ )。稍后我们将把它推广到一系列转移概率。有人以概率 T ( s → s ′ ) 提出一个举动，然后以接受概率 A ( s → s ′ ) 接受或拒绝该举动。详细平衡和遍历性足以确保随机游走在足够多的迭代之后将收敛到 π ( s ) ，其中详细平衡的意思是：