XiaoMi-AI文件搜索系统
World File Search System2024年5月27日,日本陆上自卫队金泽驻地……
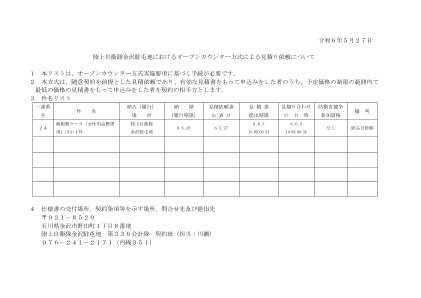
计算出的金额(若金额有不足1日元的小数部分,则小数部分向下舍去)即为认定金额,因此无论估价师是消费税、地方消费税的纳税事业体还是免税事业体,投标人均须输入估价金额的110/100。在团队设定的估价范围内,估价金额最低的投标人即为认定者。如果有两名或两名以上的申请人提供最低投标价,则通过抽签方式确定投标人。 6. 合同的准备 被选定为承包方的一方应在选定后立即按照《驻军使用标准合同》准备合同等。但是,合同金额未满50万日元时,无需准备合同。 7.其他(1)招标及承包指南应符合中央军队网站的标准招标指南。
1 2 3 1 扶手安装支架和 4 个其他物品 Kochi Garrison 6.7。......
以上内容,在接受《投标及合同指南》、《开放式柜台方式实施指南》、《标准合同等》的合同条款等后,我们将提供报价。 此外,本公司(若为个人则为本人,若为团体则为本公司组织)特此同意《投标及合同指南》中关于排除黑社会性质组织的承诺。
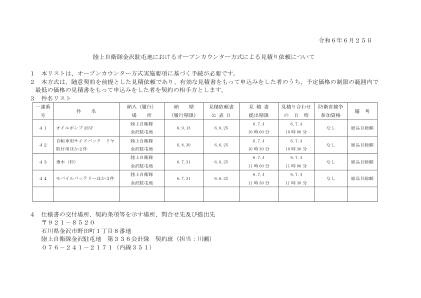
2024年6月25日,日本陆上自卫队金泽驻地……
计算出的金额(若金额有不足1日元的小数部分则将该小数部分四舍五入)即为认定金额,因此,无论估价师是消费税、地方消费税的纳税事业体还是免税事业体,投标人均须输入估价金额的110/100。在团队设定的估价范围内,估价金额最低的投标人即为认定者。如果有两名或两名以上的申请人提供最低投标价,则通过抽签方式确定投标人。 6. 合同的准备 被选定为承包方的一方应在选定后立即按照《驻军使用标准合同》准备合同等。但是,合同金额未满50万日元时,无需准备合同。 7.其他(1)招标及承包指南应符合中央军队网站的标准招标指南。
拉马努金宇宙:HPC 资源人员 - 诺伊达
关于系:物理与材料科学与工程系 (PMSE) 为 ECE、CSE、IT 和生物技术分支的 B.Tech 学生提供多门物理和材料科学基础和高级课程。该系拥有丰富的物理学博士和硕士学位课程。该系认为物理学的目标是从第一原理理解物理世界中一切事物的运作。该系结合物理学和材料科学来解决与能源、纳米技术、量子器件、光学和其他主要工程学科相关的实际问题。该系拥有配备最先进设备的研究实验室。该系专注于纳米科学和多功能纳米材料、能源和先进功能材料、原子和分子物理学、光子学和等离子体学、量子光学和量子信息、光学传感器、振动光谱、拉曼光谱、固态离子学、稀磁半导体 (自旋电子学)、热电和超导材料以及激光等离子体相互作用的研究。此外,系里的教职人员还负责指导博士后研究员。博士后研究员和大量外部资助项目的存在增强了系里的学术氛围。
什罗普郡特尔福德和雷金综合护理战略
从国家层面来看,由于公共卫生方法的改善以及治疗和医学的进步,20 世纪预期寿命不断增加的趋势在 21 世纪逐渐减缓、停滞,在某些地方甚至出现下降。虽然 2019 年有所改善,但这些改善大多被 COVID-19 大流行所抵消,导致 2020 年预期寿命急剧下降。这种模式在什罗普郡、特尔福德和雷金也很明显,这两个地区的男性预期寿命以及特尔福德和雷金的女性预期寿命似乎在 2014 年达到峰值。最新的 3 年数据(2020-2022 年)表明,女性(82.1 岁)和男性(78.0 岁)的预期寿命都比全国平均水平(女性 82.8 岁,男性 78.9 岁)短得多,比什罗普郡的邻居(女性 83.9 岁,男性 79.8 岁)短约两年,而他们自己的预期寿命与英格兰的平均寿命相似。
玛丽亚·尤金妮亚·福尔特斯·布罗洛
2018 年:MEF Brollo、PH Flores、L. Gutierrez、C. Johansson、DF Barber 和 MP Morales,《纳米粒子的磁性及其在脂质体和细胞上的空间分布的关系》,Phys. Chem. Chem. Phys.,20,17829-17838。2017 年:H. Gavilan、EH Sanchez、MEF Brollo、L. Asin、KK Moerner、C. Frandsen、FJ Lazaro、CJ Serna、S. Veintemillas-Verdaguer、MP Morales 和 L. Gutierrez,《通过多元醇介导过程合成的磁赤铁矿纳米花的形成机理》,ACS Omega,2,7172-7184。
藻酸钠/κ-carrageenan膜用于莫匹罗金真皮递送
目的:慢性伤害也是一个公共卫生问题,有必要开发和应用新材料以促进伤口愈合的更令人满意的结果。因此,这项研究旨在基于与Zn 2+交联的κ-甲rage素和藻酸钠的组合开发天然聚合物膜,以控制莫皮罗辛(MUP)。方法:使用振动光谱(拉曼和红外光谱)来表征化学结构和交联过程。微拉曼成像和扫描电子显微镜分别观察了聚合物的空间分布和样品的形态。对膜的质量,厚度和MUP浓度(MUP释放动力学及其杀菌活性)进行了分析。结果:膜在厚度,质量和MUP数量方面表现出良好的均匀性。但是,抗生素的百分比低于添加的抗生素百分比,表明在膜生产过程中损失。肿胀和释放动力学研究表明膜和受控药物输送过程的肿胀能力良好。使用抑制方法,确定了膜的抗菌活性,以金黄色葡萄球菌,大肠杆菌,表皮葡萄球菌和铜绿假单胞菌的形式确定。所有产生的薄膜均显示出对这些细菌生长的活性。结论:结果说明了在聚合物膜中使用κ-carrageenan和藻酸钠来调节MUP的潜力,目的是开发可改善伤口愈合结果的伤口敷料。
斯里尼瓦瑟·拉马努金 - 数学家,因...而闻名
助理教授 数学系,SL Bawa DAV 学院,巴塔拉 摘要 斯里尼瓦萨·拉马努金是一位印度数学家,以其在数论、连分数和无穷级数方面的开创性贡献而闻名,他仍然是数学史上最具影响力的人物之一。拉马努金 1887 年出生于殖民地印度,他基本上是自学成才,尽管受过的正规教育有限,但他还是发展了自己的数学理论。他早期在配分函数、高度合数和模形式性质方面的工作为数论的重大进步铺平了道路。拉马努金与英国数学家 GH 哈代的合作尤为卓有成效,从而发展了几个数学概念,包括著名的哈代-拉马努金数。他在无穷级数方面的工作,尤其是他的快速收敛到圆周率的级数,对数学分析和计算算法产生了深远的影响。尽管拉马努金的一生很短暂——32 岁便去世——但他的发现仍然激励着当代数学研究,尤其是在密码学、统计力学和计算机科学等领域。本文探讨了拉马努金的一生、他在数学方面的主要贡献以及他对现代数学的持久影响,展示了他的工作成果的持久遗产及其在数论和数学计算领域的相关性。